人教新课标A版2019-2020学年高一下学期必修三 3.2.1古典概型 同步练习(原创)(含答案解析)
文档属性
| 名称 | 人教新课标A版2019-2020学年高一下学期必修三 3.2.1古典概型 同步练习(原创)(含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-17 11:31:56 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2019-2020学年高一下学期必修三3.2古典概型
(时间60分钟 总分100分)
一、选择题(每小题5分,共30分)
1.一个家庭有两个小孩,则所有可能的基本事件有( )
A.(男,女),(男,男),(男,女)
B.(男,女),(男,女)
C.(男,男),(男,女),(女,男),(女,女)
D.(男,男),(女,女)
2.下列试验中,是古典概型的为( )
A.种下一粒花生,观察它是否发芽B.向正方形ABCD内任意投掷一点P,观察点P是否与正方形的中心O重合
C.从1,2,3,4四个数中任取两个数,求所取两数之一是2的概率
D.在区间[0,5]内任取一点,求此点小于2的概率
3.已知某射击运动员每次击中目标的概率都是0.8,现采用随机模拟的方法估计该运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标.以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 0293 7140 9857
0347 4373 8636 6947
1417 4698 0371 6233
2616 8045 6011 3661
9597 7424 7610 4281
根据以上数据估计该运动员射击4次,至少击中3次的概率为( )
A.0.852 B.0.8192 C.0.8 D.0.75
4.从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离不小于该正方形边长的概率为( )
A. B. C. D.
5.如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数.从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( )
A. B. C. D.
6.已知5件产品中有2件次品,其余为合格品.现从这5件产品中任取2件,恰有一件次品的概率为( )
A.0.4 B.0.6 C.0.8 D.1
二、填空题(每小题5分,共20分)
7.从1,2,3,4中随机取出两个数,则其和为奇数的概率为_______.
8.下列试验中,是古典概型的有(填序号)_______.
①向一个圆面内随机地投一个点,如果该点落在圆面内任意一点都是等可能的,观察并记录点所投的区域;
②如图所示,射击运动员向一靶心进行射击,这一试验的结果只有有限个:命中10环,命中9环,…,命中1环和命中0环(即未命中).观察射击环数;
③从1,2,3…,9中随机选取一个数,观察取到的数是否为偶数.
9.有100张卡片(从1号到100号),从中任取1张,取到的卡片的标号是7的倍数的概率是_______.
10.用红、黄、蓝三种不同颜色给如图3.2-14中的3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形颜色都相同的概率是,3个矩形颜色都不同的概率是_______.
三、解答题(共5题,共50分)
11.判断下列试验是否是古典概型:
(1)在适宜的条件下,种下一粒种子观察它是否发芽;
(2)口袋中有2个红球,2个白球,每次从中任取一球,观察颜色后放回,直到取出红球;
(3)从甲、乙、丙、丁、戊5名同学中任意抽取1名担任学生代表;
(4)射击运动员向一靶子射击5次,脱靶的次数;
(5)某小组有男生5人,女生3人,从中任选1人做演讲
12.盒中有大小形状相同的5个白球,2个黑球,用随机模拟法求下列事件的概率:
(1)任取1个球,得到白球;
(2)任取3个球,恰有2个白球;
(3)任取3个球(分三次每次放回再取),恰有3个白球.
13.从1,2,3,4,5,6中任取两个数字组成一个两位数,求组成的两位数大于50的概率。
14.某市举行职工技能比赛活动,甲厂派出2男1女共3名职工,乙厂派出2男2女共4名职工
(1)若从甲厂和乙厂报名的职工中各任选1名进行比赛,求选出的2名职工性别相同的概率;
(2)若从甲厂和乙厂报名的这7名职工中任选2名进行比赛,求选出的这2名职工来自同一工厂的概率。
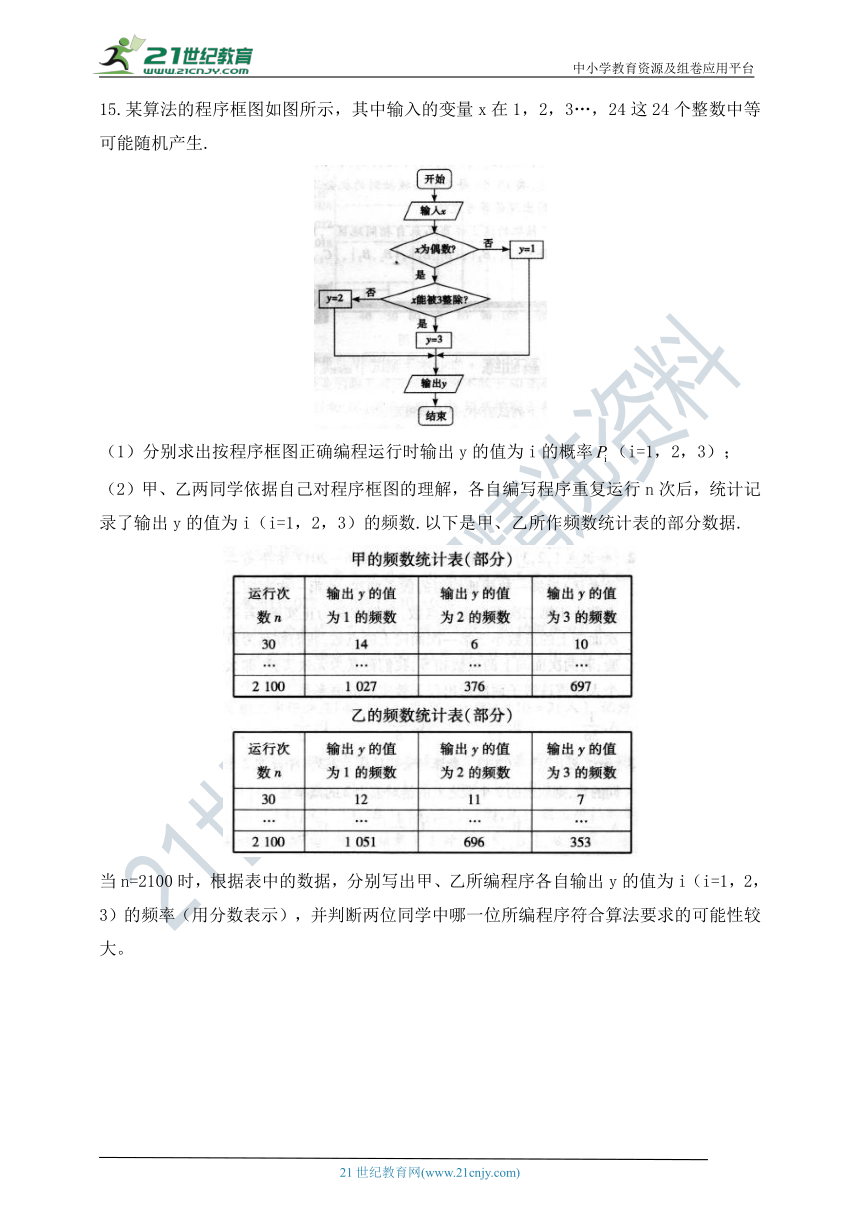
15.某算法的程序框图如图所示,其中输入的变量x在1,2,3…,24这24个整数中等可能随机产生.
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合算法要求的可能性较大。
答案
1.【解析】因为这两个小孩有先后顺序,易得所有可能的基本事件是(男,男),(男,女),(女,男),(女,女).
答案:C
2.【解析】本题考查古典概型的概念.对于A,发芽与不发芽的概率一般不相等,不满足等可能性;对于B,正方形内点的个数有无限多个,不满足有限性;对于C,满足有限性和等可能性,是古典概型;对于D,区间内的点有无限多个,不满足有限性.故选C.
答案:C
3.【解析】因为射击4次至多击中2次对应的随机数组为7140,1417,0371,6011,7610,共5组,所以射击4次,至少击中3次的概率为1-=0.75.
答案:D
4.【解析】如图可知,从5个点中选取2个点的全部情况有{0,A},10,B},{0,C},{O,D},{A,B},{A,C},{A,D},{B,C},{B,D},{C,D},共10种.选取的2个点的距离不小于该正方形边长的情况有{A,B},{A,C},{A,D},{B,C},{B,D},{C,D},共6种.故所求概率为
答案:C
5.【解析】从1,2,3,4,5中任取3个不同的数,有{1,2,3},{1,2,4},{1,2,5},{1,3,4},{1,3,5},{1,4,5},{2,3,4},{2,3,5},{2,4,5},{3,4,5},共10个基本事件,其中这3个数能构成一组勾股数的只有{3,4,5},所以所求概率为
答案:C
6.【解析】设5件产品中3件合格品分别为,2件次品分别为B1,B2,则从5件产品中任取2件的所有基本事件为,
,共10个,其中恰有一件次品包含的基本事件为,共6个,故所求的概率为.
答案:B
7.【解析】不同的取法包括{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},共6个基本事件,每个基本事件发生的可能性相同,属于古典概型。和为奇数包括{1,2},{1,4},{2,3},{3,4},共4个基本事件,故所求概率.
8.【解析】①试验的所有可能结果是圆面内的所有点,试验的结果有无限多个,因此,这个试验不是古典概型。
②试验的所有可能结果只有11个,但是命中10环,命中9环…,命中1环和命中0环(即未命中)的概率是不相等的,因此,这个试验不是古典概型.
③该试验有9种可能发生的结果,且取到每一个数的概率是相等的,因此,这个试验是古典概型.
9.【解析】满足是7的倍数的数依次为7,14,21…,98,共有14个,所以所求概率为.
10.【解析】所有可能的基本事件共有27个,如图所示:
记“3个矩形颜色都相同”为事件A,由图知,事件A中的基本事件有3个,故
。记“3个矩形颜色都不同”为事件B,由图可知,事件B中的基本事件有6个,故。
11.【解析】(1)这个试验的结果只有两个:“发芽”与“不发芽”,具备了有限性.而“发芽”与“不发芽”这两个结果出现的可能性一般是不相等的,即不具备等可能性,因此该试验不是古典概型。
(2)每次摸出一个球后,仍放回袋中,再摸一个球。显然,对于有放回抽样,依次摸出的球可以重复,且摸球可无限地进行下去,即所有可能结果有无限个,因此该试验不是古典概型。
(3)从5名同学中任意抽取1名,有5种等可能发生的结果:抽到学生甲,抽到学生乙,抽到学生丙,抽到学生了,抽到学生龙。因此该试验是古典概型。
(4)射击的结果:命中10环,命中9环…,命中0环,都是基本事件,但不是等可能事件,因此该试验不是古典概型。
(5)显然满足有限性和等可能性,因此该试验是者典概型.
12.【解析】用1,2,3,4,5表示白球,6,7表示黑球,任取3个球,即每三个数一组,每组中的数字不同;而任取3个球(分三次每次放回再取),每组中的数字可以相同。
于是,用计算器或计算机产生1到7之间的取整数,值的随机数。
(1)统计随机数个数N及小于6的个数,则即为任取1个球,得到白球的概率的近似值。
(2)三个数一组(每组中的数字不同),统计总组数M及恰有两个数字小于6的组数,则即为任取3个球,恰有2个白球的概率的近似值。
(3)三个数一组(每组中的数字可以相同),统计总组教K及三个数字都小于6的组数,则即为任取3个球(分三次每次放回再取),恰有3个白球的概率的近似值.
13.【解析】所有的基本事件是12,13,14,15,16,21,23,24,25,26,31,32,34,35,36,41,42,43,45,46,51,52,53,54,56,61,62,63,64,65,共30个.
设“组成的两位数大于50”为事件A,则事件A包含的基本事件是51,52,53,54,56,61,62,63,64,65,共10个.
14.【解析】记甲厂派出的2名男职工为,女职工为a;乙厂派出的2名男职工为,2名女职工为.
(1)从甲厂和乙厂报名的职工中各任选1名,不同的结果有
,,共12种.
其中选出的2名职工性别相同的结果有,共6种。故选出的2名职工性别相同的概率
(2)若从甲厂和乙厂报名的这7名职工中任选2名,不同的结果有
,},共21种.
15.【解析】(1)变量x是在1,2,3…,24这24个整数中等可能随机产生的一个数,共有24种可能.
当x从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时,输出y的值为1,故;
当x从2,4,8,10,14,16,20,22这8个数中产生时,输出y的值为2,故;当x从6,12,18,24这4个数中产生时,输出y的值为3,故
所以,输出y的值为1的概率为,输出y的值为2的概率为,输出y的值为3的概率为
(2)当n=2100时,甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率如下:
比较频率趋势与概率,可得乙同学所编写的程序符合算法要求的可能性较大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
