鲁教版(五四制)八年级数学下册6.1菱形的性质与判定(第2课时)课件(23张PPT)
文档属性
| 名称 | 鲁教版(五四制)八年级数学下册6.1菱形的性质与判定(第2课时)课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
6.1菱形的性质与判定(2)
菱形的判定
1.理解并掌握菱形的两个判定定理。(重点)
2.会用菱形的判定方法进行有关的证明和计算。(难点)
3.通过菱形与平行四边形判定方法的类比,进一步体会类比的思想方法。
学习目标
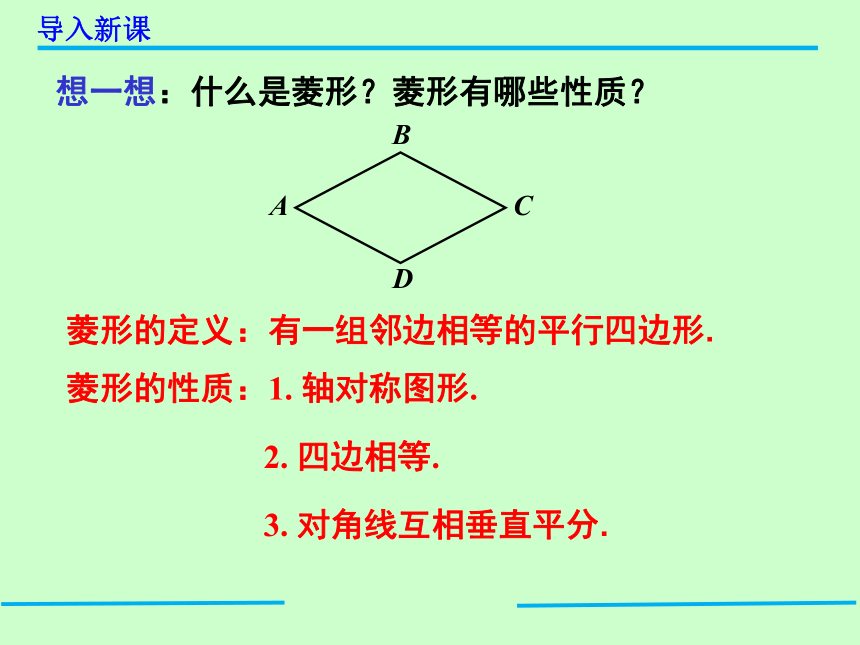
想一想:什么是菱形?菱形有哪些性质?
菱形的定义:有一组邻边相等的平行四边形.
菱形的性质:1. 轴对称图形.
2. 四边相等.
3. 对角线互相垂直平分.
导入新课
做一做
思考:剪下来的是什么图形?
将一张长方形的纸对折,再对折,沿图中的虚线剪下一个角。
问题:根据菱形的定义,邻边相等的平行四边形是菱形。除此之外,你认为还有什么条件可以判断一个平行四边形是菱形?
探究新知
想法: 对角线垂直的平行四边形是菱形,
四边相等的平行四边形是菱形。
猜想1:对角线互相垂直的平行四边形是菱形。
猜想2:四边相等的四边形是菱形。
证明猜想1
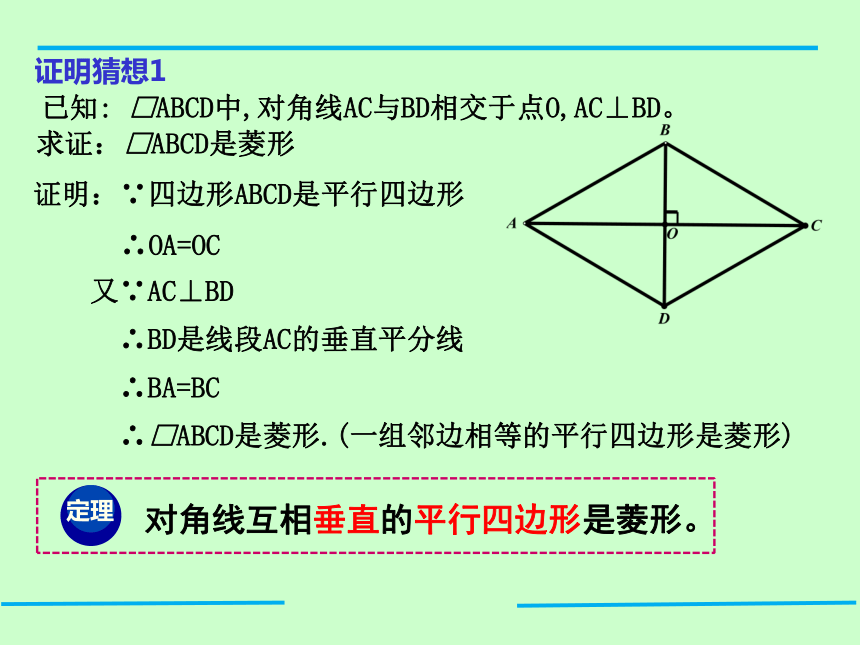
已知: □ABCD中,对角线AC与BD相交于点O,AC⊥BD。
求证:□ABCD是菱形
又∵AC⊥BD
∴BD是线段AC的垂直平分线
∴BA=BC
∴□ABCD是菱形.(一组邻边相等的平行四边形是菱形)
证明:∵四边形ABCD是平行四边形
∴OA=OC
对角线互相垂直的平行四边形是菱形。
菱形的判定定理:
(对角线)
几何语言表示:
∵AC⊥BD
∴□ABCD是菱形
判断对错
1.对角线相等且互相平分的四边形是菱形
2.对角线互相平分且垂直的四边形是菱形
3.对角线相等的四边形是菱形
4.对角线垂直的平行四边形是菱形
5.对角线互相平分的平行四边形是菱形。
练一练
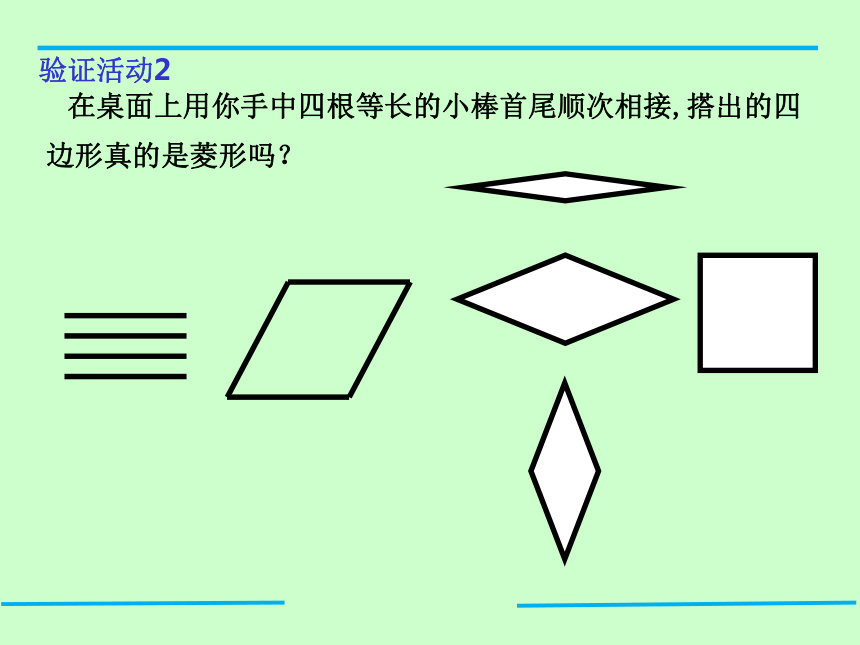
在桌面上用你手中四根等长的小棒首尾顺次相接,搭出的四边形真的是菱形吗?
验证活动2
已知:四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形。
证明:∵AB=CD,AD=BC
∴四边形ABCD是平行四边形。
又∵AD=AB
∴□ABCD是菱形。
证明猜想2
四边相等的四边形是菱形。
菱形的判定定理:
(四边关系)
几何语言表示:
∵AB=BC=CD=DA
∴四边形ABCD是菱形
典例精讲
例1.已知:在□ABCD中,对角线AC与BD相交于点O,AB= ,OA=2,OB=1
求证:□ABCD是菱形。
证明:在△AOB中,
∵
∴OA2+OB2=AB2
∴△AOB是直角三角形, ∠AOB=90°
∴AC⊥BD
∴□ABCD是菱形
例2.已知:在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与AD,AC,BC相交于E,O,F。
求证:四边形AFCE是菱形。
1
2
AD∥BC 角相等
EF⊥AC
OA=OC
EF垂直平分线AC
分析:
1
2
证明:
∴AE=CF
∵AE∥CF
∴四边形AFCE是平行四边形
∵AC⊥EF
∴□ AFCE是菱形
1.木工师傅为装修房间,需要从一块平行四边形木板中截出一块菱形材料,你能帮帮他吗?
A
B
C
D
AM = AD
M
MN∥AD
AM∥DN
回归生活
A
C
B
D
2.已知线段AC,你能用尺规作图的方法作一个
菱形ABCD,使AC为菱形的一条对角线吗?
O
E
F
一组邻边相等的平行四边形叫做菱形。
定理1:对角线互相垂直的平行四边
是菱形。(对角线)
定理2:四边相等的四边形是菱形。
(四边关系)
菱形的判定
定义
定理
课堂小结
当堂达标
1.在□ABCD中,添加下列条件不能判定□ABCD是
菱形的是( )
(A)AB=BC (B)AC⊥BD (C)AC=BD (D)BD平分∠ABC
C
2.你能画出一个对角线的长分别是6cm和8cm的菱形吗?它的边长是 ,周长是 , 面积是 。
5cm
20cm
24cm2
4.在菱形ABCD中,对角线AC与BD相交于点O,点E,F,G,H分别是OA,OB,OC,OD的中点。
求证:四边形EFGH是菱形
3.如图,已知□ABCD的对角线相交于点O且AC=BD,
DE∥AC,CE ∥BD.
求证:四边形OCED是菱形
课后作业
1.如图所示,下列条件:①AC⊥BD②∠BAD=90°③CD=BC④AB⊥AC。其中能单独判定平行四边形ABCD是菱形的是( )
(A)①③ (B)②③ (C)③④ (D)②
2.如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F。试问四边形AEDF是菱形吗?为什么?
3.已知:如图,△AOD, △AOB, △COB, △COD是四个彼此全等的三角形,
求证:四边形ABCD是菱形
4.如图,在四边形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连接C′E。
你能确定四边形CDC′E的形状吗?证明你的结论。
6.1菱形的性质与判定(2)
菱形的判定
1.理解并掌握菱形的两个判定定理。(重点)
2.会用菱形的判定方法进行有关的证明和计算。(难点)
3.通过菱形与平行四边形判定方法的类比,进一步体会类比的思想方法。
学习目标
想一想:什么是菱形?菱形有哪些性质?
菱形的定义:有一组邻边相等的平行四边形.
菱形的性质:1. 轴对称图形.
2. 四边相等.
3. 对角线互相垂直平分.
导入新课
做一做
思考:剪下来的是什么图形?
将一张长方形的纸对折,再对折,沿图中的虚线剪下一个角。
问题:根据菱形的定义,邻边相等的平行四边形是菱形。除此之外,你认为还有什么条件可以判断一个平行四边形是菱形?
探究新知
想法: 对角线垂直的平行四边形是菱形,
四边相等的平行四边形是菱形。
猜想1:对角线互相垂直的平行四边形是菱形。
猜想2:四边相等的四边形是菱形。
证明猜想1
已知: □ABCD中,对角线AC与BD相交于点O,AC⊥BD。
求证:□ABCD是菱形
又∵AC⊥BD
∴BD是线段AC的垂直平分线
∴BA=BC
∴□ABCD是菱形.(一组邻边相等的平行四边形是菱形)
证明:∵四边形ABCD是平行四边形
∴OA=OC
对角线互相垂直的平行四边形是菱形。
菱形的判定定理:
(对角线)
几何语言表示:
∵AC⊥BD
∴□ABCD是菱形
判断对错
1.对角线相等且互相平分的四边形是菱形
2.对角线互相平分且垂直的四边形是菱形
3.对角线相等的四边形是菱形
4.对角线垂直的平行四边形是菱形
5.对角线互相平分的平行四边形是菱形。
练一练
在桌面上用你手中四根等长的小棒首尾顺次相接,搭出的四边形真的是菱形吗?
验证活动2
已知:四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形。
证明:∵AB=CD,AD=BC
∴四边形ABCD是平行四边形。
又∵AD=AB
∴□ABCD是菱形。
证明猜想2
四边相等的四边形是菱形。
菱形的判定定理:
(四边关系)
几何语言表示:
∵AB=BC=CD=DA
∴四边形ABCD是菱形
典例精讲
例1.已知:在□ABCD中,对角线AC与BD相交于点O,AB= ,OA=2,OB=1
求证:□ABCD是菱形。
证明:在△AOB中,
∵
∴OA2+OB2=AB2
∴△AOB是直角三角形, ∠AOB=90°
∴AC⊥BD
∴□ABCD是菱形
例2.已知:在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与AD,AC,BC相交于E,O,F。
求证:四边形AFCE是菱形。
1
2
AD∥BC 角相等
EF⊥AC
OA=OC
EF垂直平分线AC
分析:
1
2
证明:
∴AE=CF
∵AE∥CF
∴四边形AFCE是平行四边形
∵AC⊥EF
∴□ AFCE是菱形
1.木工师傅为装修房间,需要从一块平行四边形木板中截出一块菱形材料,你能帮帮他吗?
A
B
C
D
AM = AD
M
MN∥AD
AM∥DN
回归生活
A
C
B
D
2.已知线段AC,你能用尺规作图的方法作一个
菱形ABCD,使AC为菱形的一条对角线吗?
O
E
F
一组邻边相等的平行四边形叫做菱形。
定理1:对角线互相垂直的平行四边
是菱形。(对角线)
定理2:四边相等的四边形是菱形。
(四边关系)
菱形的判定
定义
定理
课堂小结
当堂达标
1.在□ABCD中,添加下列条件不能判定□ABCD是
菱形的是( )
(A)AB=BC (B)AC⊥BD (C)AC=BD (D)BD平分∠ABC
C
2.你能画出一个对角线的长分别是6cm和8cm的菱形吗?它的边长是 ,周长是 , 面积是 。
5cm
20cm
24cm2
4.在菱形ABCD中,对角线AC与BD相交于点O,点E,F,G,H分别是OA,OB,OC,OD的中点。
求证:四边形EFGH是菱形
3.如图,已知□ABCD的对角线相交于点O且AC=BD,
DE∥AC,CE ∥BD.
求证:四边形OCED是菱形
课后作业
1.如图所示,下列条件:①AC⊥BD②∠BAD=90°③CD=BC④AB⊥AC。其中能单独判定平行四边形ABCD是菱形的是( )
(A)①③ (B)②③ (C)③④ (D)②
2.如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F。试问四边形AEDF是菱形吗?为什么?
3.已知:如图,△AOD, △AOB, △COB, △COD是四个彼此全等的三角形,
求证:四边形ABCD是菱形
4.如图,在四边形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连接C′E。
你能确定四边形CDC′E的形状吗?证明你的结论。
