北师大版八年级下册数学 1.3线段的垂直平分线(第2课时)课件(共14张PPT)
文档属性
| 名称 | 北师大版八年级下册数学 1.3线段的垂直平分线(第2课时)课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 943.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
第3节 线段的垂直平分线
(第2课时)
北师大数学八年级下册第一章 三角形的证明
上一节课我们一起学习了线段垂直平分线的性质定理与判定定理,大家还记得这两个互逆的定理吗?请回顾一下它们的文字语言、图形语言和几何语言.
前言
这一节课我们将运用以上两个定理解决以下两个问题:
1.探究三角形三边的垂直平分线的性质定理;
2.尺规作图:已知底边和底边上的高作等腰三角形;
过一点作已知直线的垂线.
知识精讲
三角形三条边的垂直平分线的性质定理:
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.?
几何语言:∵点P是△ABC三边的垂直平分线的交点,
∴A0=BO=CO.
已知:如图,在△ABC中,设AB、BC的垂直平分线交于点O.
求证:O点在AC的垂直平分线上.
C
B
A
O
证明:连接AO,BO,CO.
∵点P在线段AB的垂直平分线上,
∴OA=OB(线段垂直平分线上的点到线段两个端点的距离相等).
同理OB=OC.∴OA=OC.
∴O点在AC的垂直平分线上(到线段两个端点距离相等的点.在这条线段的垂直平分线上).
∴AB、BC、AC的垂直平分线相交于点O
探究一、
方法小结:已知线段垂直平分线上点,常连接这个点和线段的两个端点.
知识精讲
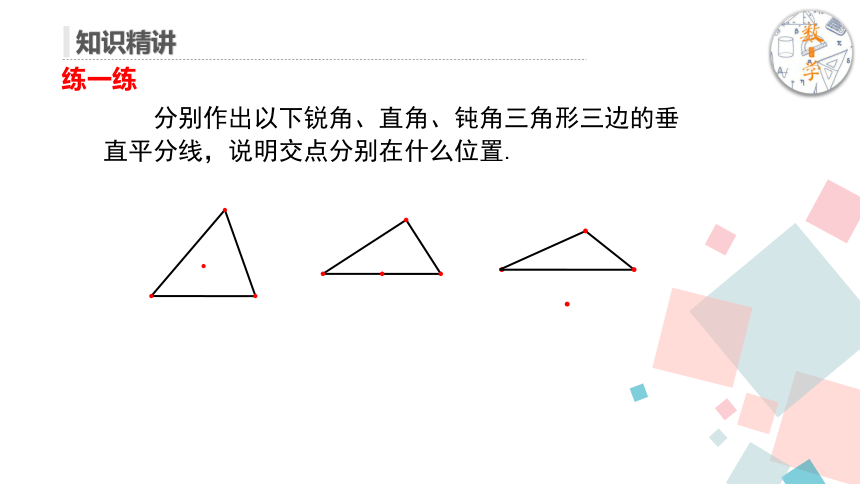
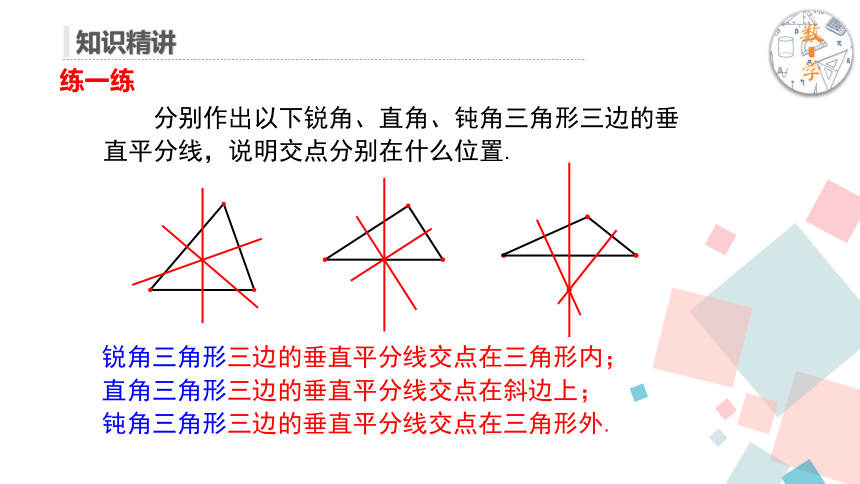
分别作出以下锐角、直角、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
练一练
锐角三角形三边的垂直平分线交点在三角形内;
直角三角形三边的垂直平分线交点在斜边上;
钝角三角形三边的垂直平分线交点在三角形外.
知识精讲
练一练
分别作出以下锐角、直角、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
知识精讲
探究二、尺规作图
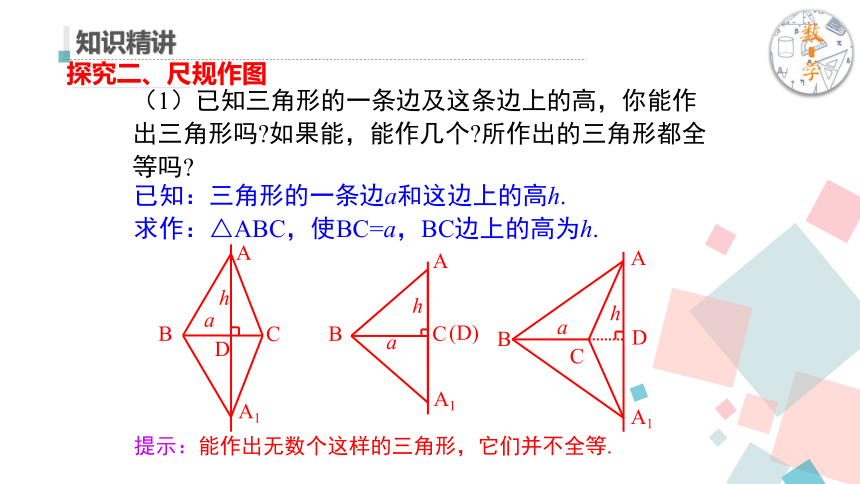
(1)已知三角形的一条边及这条边上的高,你能作出三角形吗?如果能,能作几个?所作出的三角形都全等吗?
已知:三角形的一条边a和这边上的高h.
求作:△ABC,使BC=a,BC边上的高为h.
A1
D
C
B
A
a
h
(D)
C
B
A
a
h
A1
D
C
B
A
a
h
A1
提示:能作出无数个这样的三角形,它们并不全等.
知识精讲
探究二、尺规作图
(2)已知等腰三角形的底边,你能用尺规作出等腰三角形吗?如果能,能作几个?所作出的三角形都全等吗?
这样的等腰三角形有无数多个.根据线段垂直平分线上的点到线段两个端点的距离相等,只要作底边的垂直平分线,取它上面除底边的中点外的任意一点,和底边的两个端点相连接,都可以得到一个等腰三角形.
如图所示,这些三角形不都全等.
知识精讲
(3)已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
这样的等腰三角形只有两个,并且它们是全等的,分别位于已知底边的两侧.
探究二、尺规作图
题型精讲精练
例题讲练:
例 已知:线段a,h.
求作:△ABC,使AB=AC,BC=a,高AD=h.
N
M
D
C
B
a
h
A
作法:
1.作BC=a;
2.作线段BC的垂直平分线MN交BC于D点;
3.以D为圆心,h长为半径作弧交MN于A点;
4.连接AB,AC.
△ABC就是所求作的三角形.
已知:直线 l 和 l 上一点P.
求作:PC⊥ l .
作法:
1.以点P为圆心,以任意长为半径作弧,与直线 l 相交于点A和B.
2.作线段AB的垂直平分线PC.
直线PC就是所求 l 的垂线.
题型精讲精练
1.已知直线l和其上一点P,利用尺规作 l 的垂线,使它经过点P.
A
B
C
P
l
随堂练习:
课堂测试
2.已知:线段a.
求作:△ABC,使∠ACB=90°,AC=BC=a.
作法:
(1)作直线l.
(2)在直线l上任取一条线段DE.
(3)作线段DE的垂直平分线MN交DE于C.
(4)在射线CE上截取CA=a,
在射线CM上截取CB=a.
(5)连接AB.
△ABC就是所求作的三角形.
B
A
作法:
已知直线 l 和线外一点P,利用尺规作 l 的垂线,使它经过点P.
(1)先以P为圆心,大于点P到直线 l 的垂直距离R为半径作圆,交直线 l 于A,B.
(2)分别以A、B为圆心,大于R的长
为半径作圆,相交于C、D两点.
(3)过两交点作直线 l ',此直线为
l 过P的垂线.
P ●
C
D
拓展练习:
题型精讲精练
归纳小结:
知识方法总结
1.定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
3.已知等腰三角形的底边和底边上的高作等腰三角形.
A
B
C
P
a
b
c
2.作辅助线方法:已知线段垂直平分线上点,常连接这个点和线段的两个端点.
感谢聆听,延迟开学不停学,加油,同学们!
第3节 线段的垂直平分线
(第2课时)
北师大数学八年级下册第一章 三角形的证明
上一节课我们一起学习了线段垂直平分线的性质定理与判定定理,大家还记得这两个互逆的定理吗?请回顾一下它们的文字语言、图形语言和几何语言.
前言
这一节课我们将运用以上两个定理解决以下两个问题:
1.探究三角形三边的垂直平分线的性质定理;
2.尺规作图:已知底边和底边上的高作等腰三角形;
过一点作已知直线的垂线.
知识精讲
三角形三条边的垂直平分线的性质定理:
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.?
几何语言:∵点P是△ABC三边的垂直平分线的交点,
∴A0=BO=CO.
已知:如图,在△ABC中,设AB、BC的垂直平分线交于点O.
求证:O点在AC的垂直平分线上.
C
B
A
O
证明:连接AO,BO,CO.
∵点P在线段AB的垂直平分线上,
∴OA=OB(线段垂直平分线上的点到线段两个端点的距离相等).
同理OB=OC.∴OA=OC.
∴O点在AC的垂直平分线上(到线段两个端点距离相等的点.在这条线段的垂直平分线上).
∴AB、BC、AC的垂直平分线相交于点O
探究一、
方法小结:已知线段垂直平分线上点,常连接这个点和线段的两个端点.
知识精讲
分别作出以下锐角、直角、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
练一练
锐角三角形三边的垂直平分线交点在三角形内;
直角三角形三边的垂直平分线交点在斜边上;
钝角三角形三边的垂直平分线交点在三角形外.
知识精讲
练一练
分别作出以下锐角、直角、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
知识精讲
探究二、尺规作图
(1)已知三角形的一条边及这条边上的高,你能作出三角形吗?如果能,能作几个?所作出的三角形都全等吗?
已知:三角形的一条边a和这边上的高h.
求作:△ABC,使BC=a,BC边上的高为h.
A1
D
C
B
A
a
h
(D)
C
B
A
a
h
A1
D
C
B
A
a
h
A1
提示:能作出无数个这样的三角形,它们并不全等.
知识精讲
探究二、尺规作图
(2)已知等腰三角形的底边,你能用尺规作出等腰三角形吗?如果能,能作几个?所作出的三角形都全等吗?
这样的等腰三角形有无数多个.根据线段垂直平分线上的点到线段两个端点的距离相等,只要作底边的垂直平分线,取它上面除底边的中点外的任意一点,和底边的两个端点相连接,都可以得到一个等腰三角形.
如图所示,这些三角形不都全等.
知识精讲
(3)已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
这样的等腰三角形只有两个,并且它们是全等的,分别位于已知底边的两侧.
探究二、尺规作图
题型精讲精练
例题讲练:
例 已知:线段a,h.
求作:△ABC,使AB=AC,BC=a,高AD=h.
N
M
D
C
B
a
h
A
作法:
1.作BC=a;
2.作线段BC的垂直平分线MN交BC于D点;
3.以D为圆心,h长为半径作弧交MN于A点;
4.连接AB,AC.
△ABC就是所求作的三角形.
已知:直线 l 和 l 上一点P.
求作:PC⊥ l .
作法:
1.以点P为圆心,以任意长为半径作弧,与直线 l 相交于点A和B.
2.作线段AB的垂直平分线PC.
直线PC就是所求 l 的垂线.
题型精讲精练
1.已知直线l和其上一点P,利用尺规作 l 的垂线,使它经过点P.
A
B
C
P
l
随堂练习:
课堂测试
2.已知:线段a.
求作:△ABC,使∠ACB=90°,AC=BC=a.
作法:
(1)作直线l.
(2)在直线l上任取一条线段DE.
(3)作线段DE的垂直平分线MN交DE于C.
(4)在射线CE上截取CA=a,
在射线CM上截取CB=a.
(5)连接AB.
△ABC就是所求作的三角形.
B
A
作法:
已知直线 l 和线外一点P,利用尺规作 l 的垂线,使它经过点P.
(1)先以P为圆心,大于点P到直线 l 的垂直距离R为半径作圆,交直线 l 于A,B.
(2)分别以A、B为圆心,大于R的长
为半径作圆,相交于C、D两点.
(3)过两交点作直线 l ',此直线为
l 过P的垂线.
P ●
C
D
拓展练习:
题型精讲精练
归纳小结:
知识方法总结
1.定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
3.已知等腰三角形的底边和底边上的高作等腰三角形.
A
B
C
P
a
b
c
2.作辅助线方法:已知线段垂直平分线上点,常连接这个点和线段的两个端点.
感谢聆听,延迟开学不停学,加油,同学们!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
