2020春北师大版八年级下册数学 1.1等腰三角形同步练习(共4课时 含简单答案)
文档属性
| 名称 | 2020春北师大版八年级下册数学 1.1等腰三角形同步练习(共4课时 含简单答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 08:58:24 | ||
图片预览



文档简介
2020春北师大版八下数学1.1等腰三角形同步练习
(第1课时)等腰三角形的性质
1.[2016·永州]如图1-5,点D,E分别在线段AB,AC上,CD与BE相交于点O.已知AB=AC,现添加的下列条件中,不能判定△ABE≌△ACD的是( )
图1-5
A.∠B=∠C B.AD=AE
C.BD=CE D.BE=CD
2.如图1-6,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为( )
图1-6
A.35° B.45°
C.55° D.60°
3.[2017·滨州]如图1-7,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为( )
图1-7
A.30° B.36°
C.40° D.45°
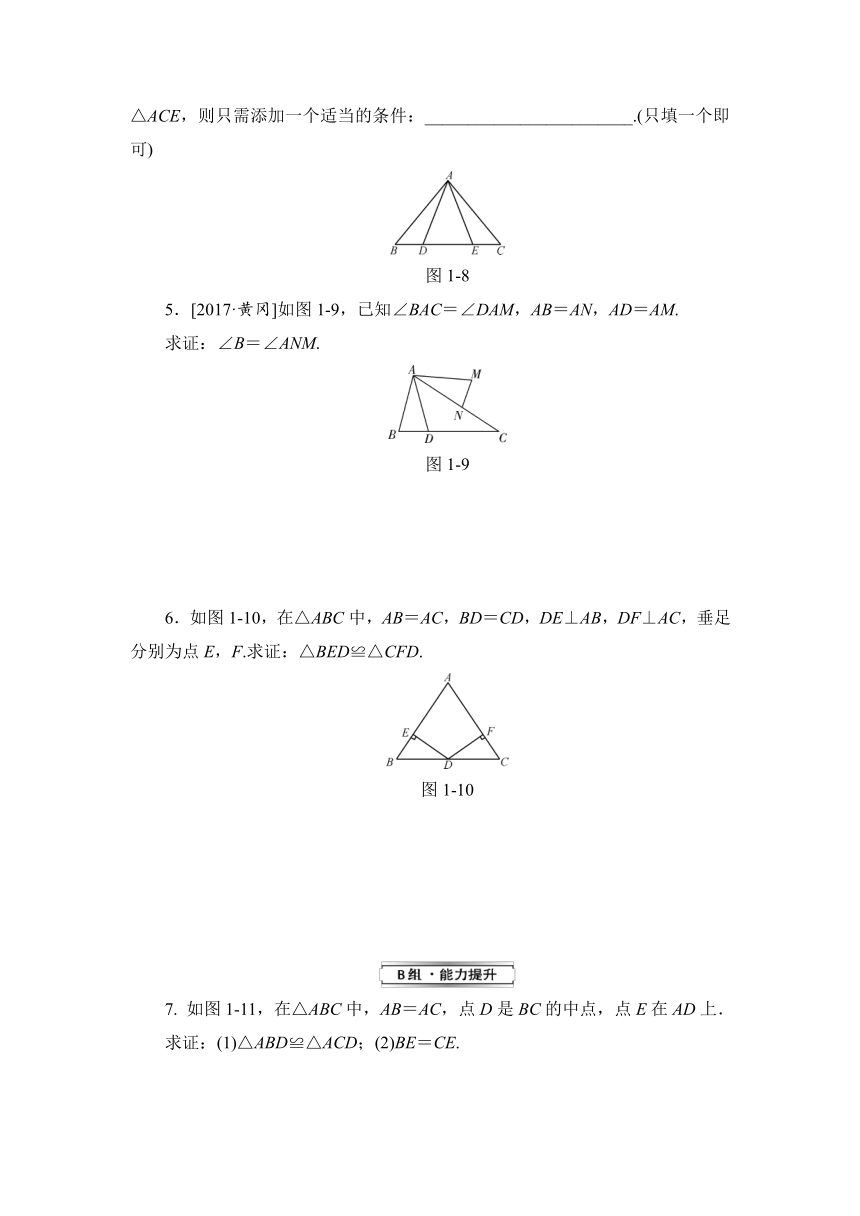
4.如图1-8,已知△ABC中,AB=AC,点D,E在BC上,要使△ABD≌△ACE,则只需添加一个适当的条件:________________________.(只填一个即可)
图1-8
5.[2017·黄冈]如图1-9,已知∠BAC=∠DAM,AB=AN,AD=AM.
求证:∠B=∠ANM.
图1-9
6.如图1-10,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E,F.求证:△BED≌△CFD.
图1-10
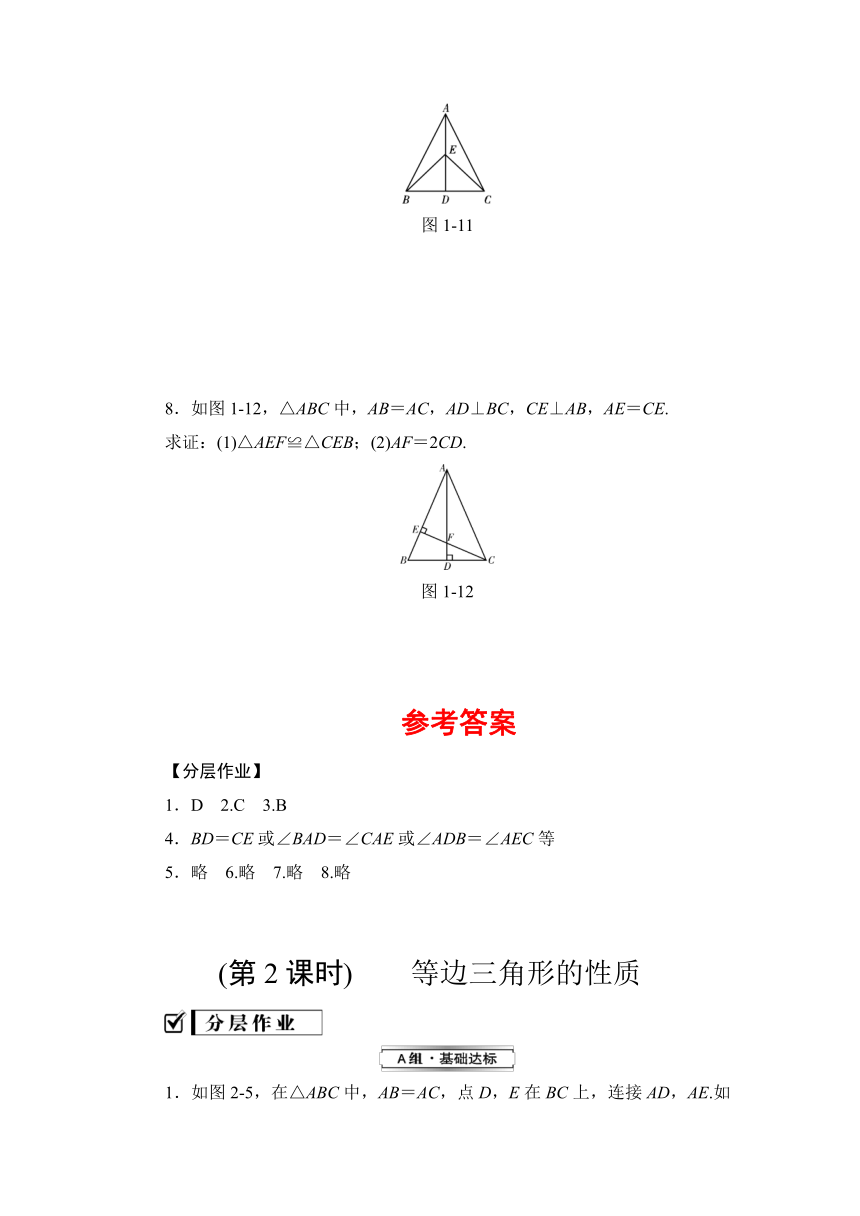
7. 如图1-11,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
求证:(1)△ABD≌△ACD;(2)BE=CE.
图1-11
8.如图1-12,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.
求证:(1)△AEF≌△CEB;(2)AF=2CD.
图1-12
参考答案
【分层作业】
1.D 2.C 3.B
4.BD=CE或∠BAD=∠CAE或∠ADB=∠AEC等
5.略 6.略 7.略 8.略
(第2课时) 等边三角形的性质
1.如图2-5,在△ABC中,AB=AC,点D,E在BC上,连接AD,AE.如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
图2-5
A.BD=CE B.AD=AE
C.DA=DE D.BE=CD
2.如图2-6,△ABC为等边三角形,AD平分∠BAC,△ADE是等边三角形,下列结论:①AD⊥BC,②EF=FD,③BE=BD,④∠ABE=60°中,正确的个数为( )
图2-6
A.4 B.3
C.2 D.1
3.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图2-7①,衣架杆OA=OB=18 cm,若衣架收拢时,∠AOB=60°,如图2-7②,则此时A,B两点之间的距离是________cm.
图2-7
4.如图2-8,已知△ABC是等边三角形,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E=________°.
图2-8
5.如图2-9,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
图2-9
6.[2016·怀化]等腰三角形的两边长分别为4 cm和8 cm,则它的周长为( )
A.16 cm B.17 cm
C.20 cm D.16 cm或20 cm
7.如图2-10,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数.
图2-10
8.如图2-11,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,FE=FD.
求证:AD=CE.
图2-11
参考答案
【分层作业】
1.C 2.A 3.18 4.15 5.(1)30° (2)4
6.C 7.15° 8.略
(第3课时) 等腰三角形的判定
1.如图3-5所示,在△ABC中,∠A=36°,∠C=72°,∠ABC的平分线交AC于点D,则图中共有等腰三角形( )
图3-5
A.0个 B.1个
C.2个 D.3个
2.如图3-6所示,在△ABC中,CD平分∠ACB,DE∥BC,交AC于点E,如果DE=7,AE=5,则AC= .
图3-6
3.如图3-7所示,在△ABC中,AB=AC,过∠ABC和∠ACB的平分线交点O作DE∥BC,交AB于点D,交AC于点E,则图中的等腰三角形分别是
________________________________________________.
图3-7
4.已知:如图3-8所示,AB∥CD,AB∥EF.用反证法证明CD∥EF.
图3-8
5.[2017·北京]如图3-9,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D.
求证:AD=BC.
图3-9
6.如图3-10,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
图3-10
7.如图3-11,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
图3-11
参考答案
【分层作业】
1.D 2.12
3.△ADE,△BDO,△COE,△BOC,△ABC
4.略 5.略
6.(1)略 (2)△OEF为等腰三角形,理由略
7.(1)①② ①③ (2)略
(第4课时) 等边三角形的判定及30°直角三角形的性质
1.下列推理错误的是( )
A.在△ABC中,∵∠A=∠B=∠C,∴△ABC为等边三角形
B.在△ABC中,∵AB=AC,且∠B=∠C,∴△ABC为等边三角形
C.在△ABC中,∵∠A=60°,∠B=60°,∴△ABC为等边三角形
D.在△ABC中,∵AB=AC,∠B=60°,∴△ABC为等边三角形
2.如图4-5所示,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,点B恰好落在AB的中点E处,则∠A等于( )
A.25° B.30°
C.45° D.60°
图4-5
3.[2017春·新化县期末]如图4-6,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60° 500 m处,那么水塔所在的位置到公路的距离AB是________m.
图4-6
4.如图4-7所示,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,若BC=2,则BE+FC=________.
图4-7
5.如图4-8,为了响应建设社会主义新农村的号召,某村在小山顶D处建成了卫星接收发射塔AD.在B处测得∠DBC=30°,∠ABC=60°.现已测得塔高AD是42 m,则小山高CD为________.
图4-8
6.如图4-9,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.若∠B=30°,CD=1,求BD的长.
图4-9
7.如图4-10,已知△ABC中,∠ACB=120°,CE平分∠ACB,AD∥EC,交BC的延长线于点D.
(1)求∠BCE的度数;
(2)试找出图中的等边三角形,并说明理由.
图4-10
8.如图4-11,在等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,△APQ是什么形状的三角形?试证明你的结论.
图4-11
参考答案
【分层作业】
1.B 2.B 3.250 4.1 5.21 m 6.2
7.(1)60° (2)△ACD是等边三角形,理由略
8.△APQ为等边三角形,证明略.
(第1课时)等腰三角形的性质
1.[2016·永州]如图1-5,点D,E分别在线段AB,AC上,CD与BE相交于点O.已知AB=AC,现添加的下列条件中,不能判定△ABE≌△ACD的是( )
图1-5
A.∠B=∠C B.AD=AE
C.BD=CE D.BE=CD
2.如图1-6,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为( )
图1-6
A.35° B.45°
C.55° D.60°
3.[2017·滨州]如图1-7,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为( )
图1-7
A.30° B.36°
C.40° D.45°
4.如图1-8,已知△ABC中,AB=AC,点D,E在BC上,要使△ABD≌△ACE,则只需添加一个适当的条件:________________________.(只填一个即可)
图1-8
5.[2017·黄冈]如图1-9,已知∠BAC=∠DAM,AB=AN,AD=AM.
求证:∠B=∠ANM.
图1-9
6.如图1-10,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E,F.求证:△BED≌△CFD.
图1-10
7. 如图1-11,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
求证:(1)△ABD≌△ACD;(2)BE=CE.
图1-11
8.如图1-12,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.
求证:(1)△AEF≌△CEB;(2)AF=2CD.
图1-12
参考答案
【分层作业】
1.D 2.C 3.B
4.BD=CE或∠BAD=∠CAE或∠ADB=∠AEC等
5.略 6.略 7.略 8.略
(第2课时) 等边三角形的性质
1.如图2-5,在△ABC中,AB=AC,点D,E在BC上,连接AD,AE.如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
图2-5
A.BD=CE B.AD=AE
C.DA=DE D.BE=CD
2.如图2-6,△ABC为等边三角形,AD平分∠BAC,△ADE是等边三角形,下列结论:①AD⊥BC,②EF=FD,③BE=BD,④∠ABE=60°中,正确的个数为( )
图2-6
A.4 B.3
C.2 D.1
3.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图2-7①,衣架杆OA=OB=18 cm,若衣架收拢时,∠AOB=60°,如图2-7②,则此时A,B两点之间的距离是________cm.
图2-7
4.如图2-8,已知△ABC是等边三角形,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E=________°.
图2-8
5.如图2-9,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
图2-9
6.[2016·怀化]等腰三角形的两边长分别为4 cm和8 cm,则它的周长为( )
A.16 cm B.17 cm
C.20 cm D.16 cm或20 cm
7.如图2-10,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数.
图2-10
8.如图2-11,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,FE=FD.
求证:AD=CE.
图2-11
参考答案
【分层作业】
1.C 2.A 3.18 4.15 5.(1)30° (2)4
6.C 7.15° 8.略
(第3课时) 等腰三角形的判定
1.如图3-5所示,在△ABC中,∠A=36°,∠C=72°,∠ABC的平分线交AC于点D,则图中共有等腰三角形( )
图3-5
A.0个 B.1个
C.2个 D.3个
2.如图3-6所示,在△ABC中,CD平分∠ACB,DE∥BC,交AC于点E,如果DE=7,AE=5,则AC= .
图3-6
3.如图3-7所示,在△ABC中,AB=AC,过∠ABC和∠ACB的平分线交点O作DE∥BC,交AB于点D,交AC于点E,则图中的等腰三角形分别是
________________________________________________.
图3-7
4.已知:如图3-8所示,AB∥CD,AB∥EF.用反证法证明CD∥EF.
图3-8
5.[2017·北京]如图3-9,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D.
求证:AD=BC.
图3-9
6.如图3-10,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
图3-10
7.如图3-11,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
图3-11
参考答案
【分层作业】
1.D 2.12
3.△ADE,△BDO,△COE,△BOC,△ABC
4.略 5.略
6.(1)略 (2)△OEF为等腰三角形,理由略
7.(1)①② ①③ (2)略
(第4课时) 等边三角形的判定及30°直角三角形的性质
1.下列推理错误的是( )
A.在△ABC中,∵∠A=∠B=∠C,∴△ABC为等边三角形
B.在△ABC中,∵AB=AC,且∠B=∠C,∴△ABC为等边三角形
C.在△ABC中,∵∠A=60°,∠B=60°,∴△ABC为等边三角形
D.在△ABC中,∵AB=AC,∠B=60°,∴△ABC为等边三角形
2.如图4-5所示,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,点B恰好落在AB的中点E处,则∠A等于( )
A.25° B.30°
C.45° D.60°
图4-5
3.[2017春·新化县期末]如图4-6,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60° 500 m处,那么水塔所在的位置到公路的距离AB是________m.
图4-6
4.如图4-7所示,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,若BC=2,则BE+FC=________.
图4-7
5.如图4-8,为了响应建设社会主义新农村的号召,某村在小山顶D处建成了卫星接收发射塔AD.在B处测得∠DBC=30°,∠ABC=60°.现已测得塔高AD是42 m,则小山高CD为________.
图4-8
6.如图4-9,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.若∠B=30°,CD=1,求BD的长.
图4-9
7.如图4-10,已知△ABC中,∠ACB=120°,CE平分∠ACB,AD∥EC,交BC的延长线于点D.
(1)求∠BCE的度数;
(2)试找出图中的等边三角形,并说明理由.
图4-10
8.如图4-11,在等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,△APQ是什么形状的三角形?试证明你的结论.
图4-11
参考答案
【分层作业】
1.B 2.B 3.250 4.1 5.21 m 6.2
7.(1)60° (2)△ACD是等边三角形,理由略
8.△APQ为等边三角形,证明略.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
