2020春北师大版八年级下册数学 第1章1.4角平分线同步练习(共2课时 含简单答案)
文档属性
| 名称 | 2020春北师大版八年级下册数学 第1章1.4角平分线同步练习(共2课时 含简单答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 08:59:45 | ||
图片预览

文档简介
2020春北师大版八下数学第1章1.4角平分线同步练习
(第1课时)角平分线的性质定理及其逆定理
1.[2017·枣庄]如图11-6,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
图11-6
A.15 B.30
C.45 D.60
2.[2017春·碑林区校级期末]如图11-7,在△ABC中,BD平分∠ABC,DE⊥AB交AB于点E,DF⊥BC交BC于点F,若AB=12 cm,BC=18 cm,S△ABC=90 cm2,则DF的长为( )
A.3 cm B.6 cm
C.9 cm D.12 cm
图11-7
图11-8
3.如图11-8,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若AD=4,CD=2,则AB的长是 4 .
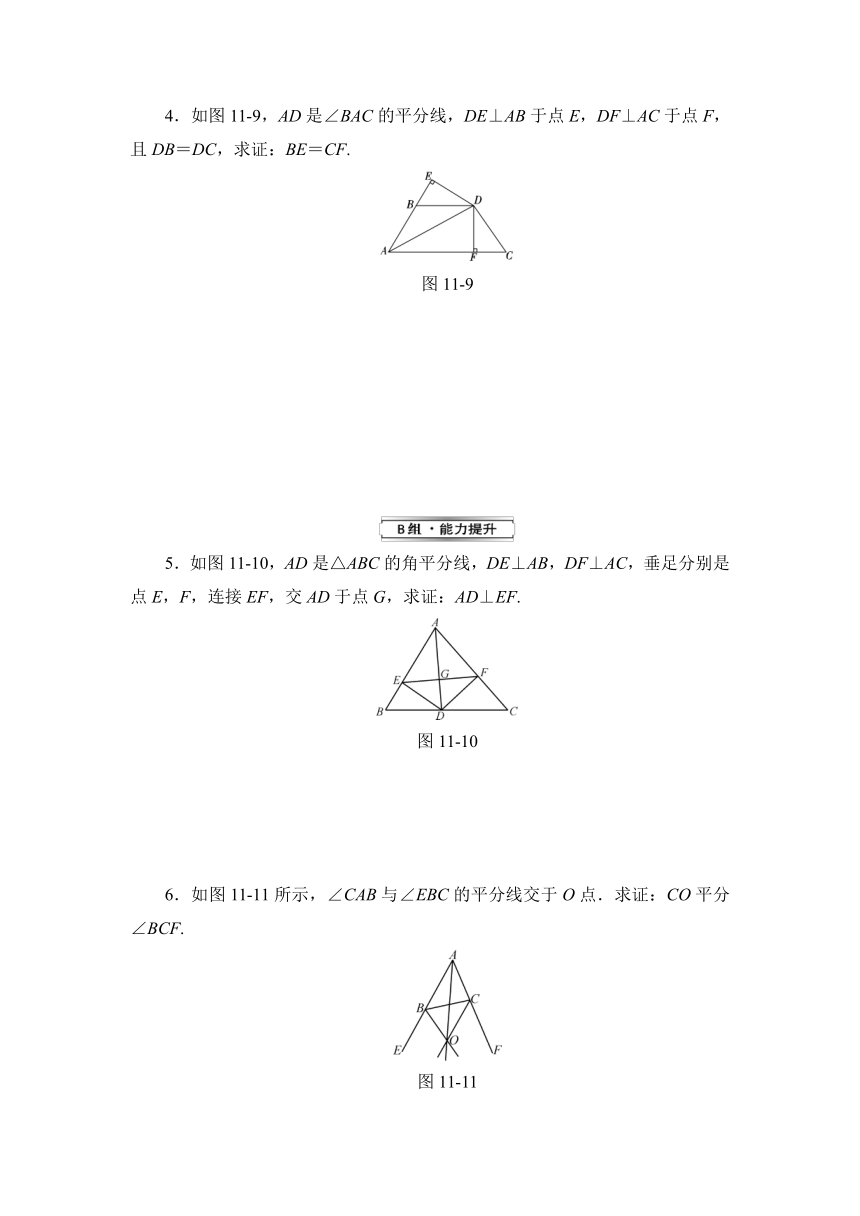
4.如图11-9,AD是∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,且DB=DC,求证:BE=CF.
图11-9
5.如图11-10,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是点E,F,连接EF,交AD于点G,求证:AD⊥EF.
图11-10
6.如图11-11所示,∠CAB与∠EBC的平分线交于O点.求证:CO平分∠BCF.
图11-11
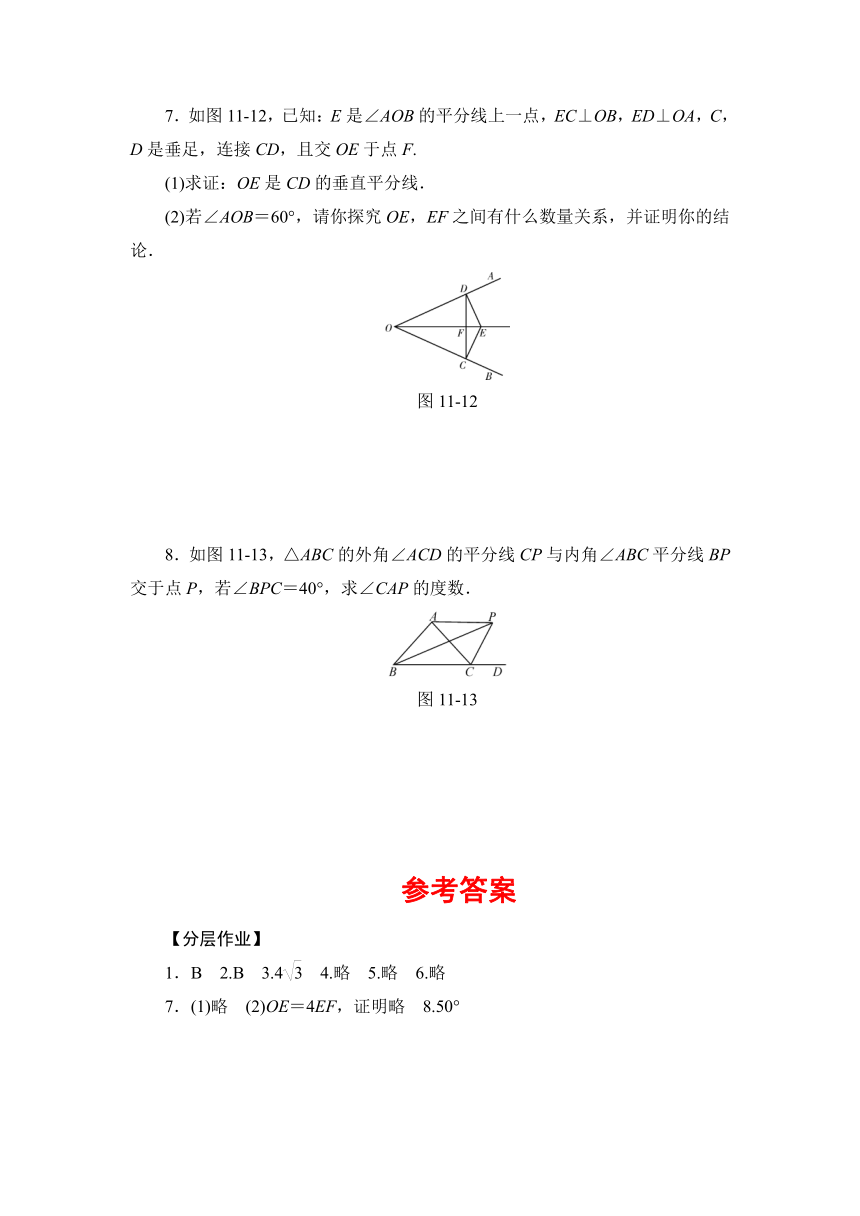
7.如图11-12,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C,D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系,并证明你的结论.
图11-12
8.如图11-13,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAP的度数.
图11-13
参考答案
【分层作业】
1.B 2.B 3.4 4.略 5.略 6.略
7.(1)略 (2)OE=4EF,证明略 8.50°
(第2课时)三角形的三条角平分线
1.如图12-6所示,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是( )
图12-6
A.3 B.4
C.6 D.5
2.如图12-7,△ABC中,∠C=90°,AO平分∠BAC,OD⊥AB,BD=3,OB=5,则BC=________.
图12-7
3.如图12-8所示,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,且平分AB.若DC=3,AC=3.
(1)求证CD=DE;(2)求BC的长.
图12-8
4.如图12-9,△ABC中,∠C=90°,AC=3,BC=4,在BC边上找一点P,使得点P到点C的距离与点P到边AB的距离相等.
(1)找出点P的位置(尺规作图).
(2)求BP的长.
图12-9
5.[2016秋·西城区校级期中]小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个锐角的平分线.如图12-10,一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”你认为小明的想法正确吗?请说明理由.
图12-10
6.已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于C,D,PC和PD有怎样的数量关系?请说明理由.
图12-11
参考答案
【分层作业】
1.A 2.9 3.(1)略 (2)9
4.(1)略 (2)2.5 5.小明的想法正确,理由略.
6.PC=PD,理由略.
(第1课时)角平分线的性质定理及其逆定理
1.[2017·枣庄]如图11-6,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
图11-6
A.15 B.30
C.45 D.60
2.[2017春·碑林区校级期末]如图11-7,在△ABC中,BD平分∠ABC,DE⊥AB交AB于点E,DF⊥BC交BC于点F,若AB=12 cm,BC=18 cm,S△ABC=90 cm2,则DF的长为( )
A.3 cm B.6 cm
C.9 cm D.12 cm
图11-7
图11-8
3.如图11-8,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若AD=4,CD=2,则AB的长是 4 .
4.如图11-9,AD是∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,且DB=DC,求证:BE=CF.
图11-9
5.如图11-10,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是点E,F,连接EF,交AD于点G,求证:AD⊥EF.
图11-10
6.如图11-11所示,∠CAB与∠EBC的平分线交于O点.求证:CO平分∠BCF.
图11-11
7.如图11-12,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C,D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系,并证明你的结论.
图11-12
8.如图11-13,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAP的度数.
图11-13
参考答案
【分层作业】
1.B 2.B 3.4 4.略 5.略 6.略
7.(1)略 (2)OE=4EF,证明略 8.50°
(第2课时)三角形的三条角平分线
1.如图12-6所示,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是( )
图12-6
A.3 B.4
C.6 D.5
2.如图12-7,△ABC中,∠C=90°,AO平分∠BAC,OD⊥AB,BD=3,OB=5,则BC=________.
图12-7
3.如图12-8所示,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,且平分AB.若DC=3,AC=3.
(1)求证CD=DE;(2)求BC的长.
图12-8
4.如图12-9,△ABC中,∠C=90°,AC=3,BC=4,在BC边上找一点P,使得点P到点C的距离与点P到边AB的距离相等.
(1)找出点P的位置(尺规作图).
(2)求BP的长.
图12-9
5.[2016秋·西城区校级期中]小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个锐角的平分线.如图12-10,一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”你认为小明的想法正确吗?请说明理由.
图12-10
6.已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于C,D,PC和PD有怎样的数量关系?请说明理由.
图12-11
参考答案
【分层作业】
1.A 2.9 3.(1)略 (2)9
4.(1)略 (2)2.5 5.小明的想法正确,理由略.
6.PC=PD,理由略.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
