2020春北师大版八年级下册数学 1.4角平分线教学课件(共2课时 29张PPT)
文档属性
| 名称 | 2020春北师大版八年级下册数学 1.4角平分线教学课件(共2课时 29张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 20.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览






文档简介
课件29张PPT。
第四节 角平分线
第1课时
北师大数学八年级下册第一章 三角形的证明
我们一起回顾一下,我们已经学习了哪些有关角平分线的知识?1.在七年级我们知道了一个角的角平分线能够把这个角分成两个相等的角。反过来,从角的顶点引出一条射线,这条射线如果把这个角分成了两个相等的角,这条射线是这个角的角平分线。
2.知道了如何用尺规作图的方法去作一个角的角平分线。角平分线的性质定理:角平分线上的点到这个角的 两边的距离相等.几何语言:∵点P在∠AOB的角平分线上,PE⊥OA,PD⊥OB,
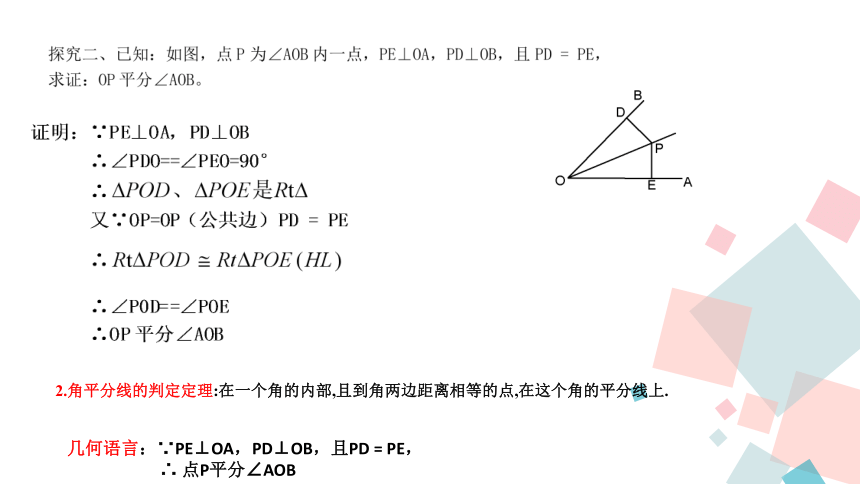
∴PD=PE?2.角平分线的判定定理:在一个角的内部,且到角两边距离相等的点,在这个角的平分线上.几何语言:∵PE⊥OA,PD⊥OB,且PD = PE,
∴ 点P平分∠AOB角平分线的性质定理:角平分线上的点到这个角的两边的距离相等.?
角平分线的判定定理:在一个角的内部,且到角两边距离相等的点,在这个角的平分线上思考:大家观察角平分线的性质定理与判定定理之间有什么?互逆关系例题讲练:例1. 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,
DE⊥AB于点E,点F在AC上,BD=DF.
求证:(1)CF=EB; (2)AB=AF+2EB.证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC.
在Rt△DCF和Rt△DEB中,
∴ Rt△DCF≌Rt△DEB(HL). ∴ CF=EB.
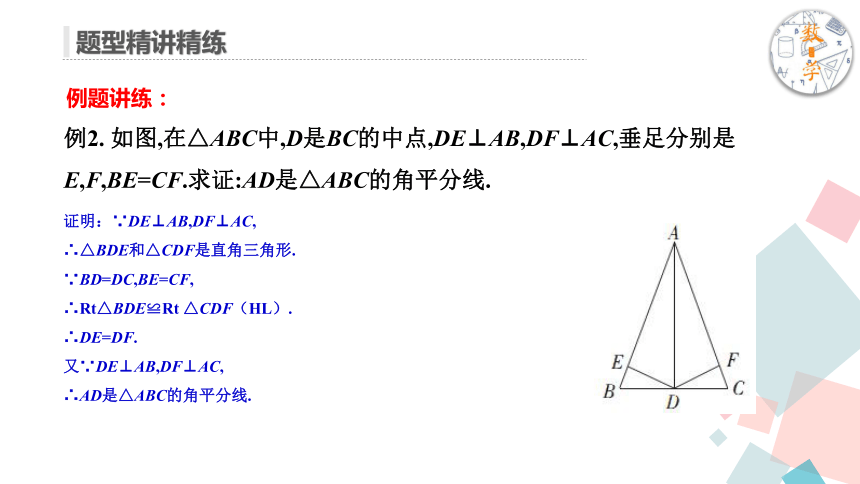
例题讲练:例题讲练:例2. 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.求证:AD是△ABC的角平分线.证明:∵DE⊥AB,DF⊥AC,
∴△BDE和△CDF是直角三角形.
∵BD=DC,BE=CF,
∴Rt△BDE≌Rt △CDF(HL).
∴DE=DF.
又∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.随堂练习:练习. 已知:如图,OC是∠AOB的平分线,点P在OC上,
PD⊥OA,PE⊥OB,垂足分别为D、E.
求证:PD=PE.证明:∵∠1=∠2,OP=OP,∠PDO=∠PEO=90°,
∴△PDO≌△PEO(AAS).
∴PD=PE(全等三角形的对应边相等).1.已知:在△AOB内部有一点P,且PD上OA,PE⊥OB,D、E为垂足且PD=PE,
求证:点P在△AOB的角平分线上. 证明:PD⊥OA,PE⊥OB,
∴∠PDO=∠ PEO=90°.
在Rt△ODP和Rt△OEP中
OP=OP,PD=PE,∴Rt△ODP ≌ Rt△OEP(HL定理).
∴∠1=∠2(全等三角形对应角相等).2.如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求 DE 的长.
?归纳小结:1.角平分线的性质定理:
角平分线上的点到这个角的两边的距离相等.?
2.角平分线的判定定理:
在一个角的内部,且到角两边距离相等的点,在这个角的平分线上.
第四节 角平分线
第2课时
北师大数学八年级下册第一章 三角形的证明
上一节课我们一起学习了角平分线的性质定理与判定定理,大家还记得这两个互逆的定理吗?请在脑海里回顾一下它们的文字语言、图形语言和几何语言.这一节课我们将学习三角形三个内角的角平分线的性质定理,并要运用三角形三条内角的角平分线的性质来解决实际问题.1.三角形三条角平分线的性质定理:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.?几何语言:∵点P是△ABC的三条角平分线的交点,且PE⊥BC,PF⊥AC,PD⊥AB,
∴PD=PE=PF. 请作出下面3个三角形的每个内角的角平分线.通过作图,大家发现了什么?2.三角形三个内角平分线的交点只有一个,实际作图时,只需作出两个角的平分线,第三个角的平分线必过这两条角平分线的交点.思考:前面我们学习了三角形各边的中垂线的性质,你能把三角形的内角平分线性质和三角形中垂线性进行一下比较吗?3.利用面积法求距离的方法:三角形角平分线的交点与三个顶点的连线,把原三角形分割成了三个小三角形,利用小三角形的面积之和等于原三角形的面积,是求角平分线交点到三边距离的常用方法.例题讲练:例1. 如图,在△ABC中,E是∠BAC,∠CBD的平分线的交点.
求证:点E在外角∠BCF的平分线上.证明:过点E作EG⊥AB,EH⊥BC,EP⊥AC,垂足分别为G, H, P.
∵AE平分∠BAC,
EG⊥AB,EP⊥AC,
∴EG=EP.
∵BE平分∠CBG,EG⊥AB,EH⊥BC,
∴EG=EH.
∴EH=EP,
又∵EP⊥AC,EH⊥BC,
∴点E在∠BCF的平分线上.例题讲练:例2. 如图,在等腰直角△ABC中,∠C=90°,AC=BC,AD平分∠BAC,DE⊥AB于E.
(1)求证:BD+DE=AC;
(2)已知AB=15 cm,求△DBE的周长;
(3)已知AC=4 cm,求CD的长.(1)证明:∵AD平分∠BAC,DE⊥AB,∠C=90°, ∴CD=DE.
∵BC=BD+CD, ∴BC=BD+DE.
∵AC=BC, ∴AC=BD+DE.例题讲练:(2)解:∵CD=DE,AD=AD,∠C= ∠AED=90°,
∴Rt△ACD≌ Rt△AED(HL), ∴AC=AE.
∵AC=BD+DE,∴BD+DE=AE.
∴△BDE的周长=BD+DE+BE=AE+BE=AB=15(cm).随堂练习:练习1. 如图,在△ABC中.AC=BC,∠C=90°,AD是△ABC的角
平分线,DE⊥AB,垂足为E.(1)已知CD=4 cm,求AC的长;
(2)求证:AB=AC+CD.【分析】本例需要运用前面所学的多个定理,而且将计算和证明融合在一起,目的是使学生进一步理解、掌握这些知识和方法,并能综合运用它们解决问题.(1)中,求AC的长,需求出BC的长,而BC=CD+DB,CD=4 cm,而BD在等腰直角三角形DBE中,根据角平分线的性质,DE=CD=4cm,再根据勾股定理便可求出DB的长.(2)中,求证AB=AC+CD.利用转化的思想AB=AE+BE,所以需证AC=AE,CD=BE.(1)解:∵AD是△ABC的角平分线,∠C=90°,DE⊥AB.
∴DE=CD=4cm(角平分线上的点到这个角两边的距离相等).
∵∠AC=∠BC ∴∠B=∠BAC(等边对等角).∵∠C=90°,∴∠B=×90°=45°.∴∠BDE=90°—45°=45°.
∴BE=DE(等角对等边).
在等腰直角三角形BDE中,BD=2DE2.=4 2 cm(勾股定理),
∴AC=BC=CD+BD=(4+42)cm.
(2)证明:由(1)的求解过程可知,Rt△ACD≌Rt△AED(HL定理)
∴AC=AE.
∵BE=DE=CD,∴AB=AE+BE=AC+CD.1.已知:如图,P是△AOB平分线上的一点,PC⊥OA,PD⊥OB,垂足分别为C、D.求证:(1)OC=OD;(2)OP是CD的垂直平分线. 证明:(1)P是∠AOB角平分线上的一点,PC⊥OA,PD⊥OB,
∴PC=PD(角平分线上的点到角两边的距离相等).
在Rt△OPC和Rt△OPD中,OP=OP,PC=PD,
∴Rt△OPC≌Rt△OPD(HL定理).
∴OC=OD(全等三角形对应边相等).
(2)又OP是∠AOB的角平分线,
∴OP是CD的垂直平分线(等腰三角形“三线合一”定理).2.如图,∠AOQ=35°,QC⊥OA于C,QD⊥OB于D,
若QC=QD,则∠AOB= °.
证明:∵QC⊥OA于C,QD⊥OB于D,QC=QD
∴ OQ是∠AOB的平分线,
∵∠AOQ=35°,
∴∠AOB=2∠AOQ=70°
故答案为70.归纳小结:1.三角形三条角平分线的性质定理:三角形的三条角平分线相交于一点,并且这一点到 三条边 的距离相等.?
2.三角形三个内角平分线的交点只有一个,实际作图时,只需作出两个角的平分线,第三个角的平分线必过这两条角平分线的交点.
3.利用面积法求距离的方法:三角形角平分线的交点与三个顶点的连线,把原三角形分割成了三个小三角形,利用小三角形的面积之和等于原三角形的面积,是求角平分线交点到三边距离的常用方法. 感谢聆听,延迟开学不停学,加油,同学们!
第四节 角平分线
第1课时
北师大数学八年级下册第一章 三角形的证明
我们一起回顾一下,我们已经学习了哪些有关角平分线的知识?1.在七年级我们知道了一个角的角平分线能够把这个角分成两个相等的角。反过来,从角的顶点引出一条射线,这条射线如果把这个角分成了两个相等的角,这条射线是这个角的角平分线。
2.知道了如何用尺规作图的方法去作一个角的角平分线。角平分线的性质定理:角平分线上的点到这个角的 两边的距离相等.几何语言:∵点P在∠AOB的角平分线上,PE⊥OA,PD⊥OB,
∴PD=PE?2.角平分线的判定定理:在一个角的内部,且到角两边距离相等的点,在这个角的平分线上.几何语言:∵PE⊥OA,PD⊥OB,且PD = PE,
∴ 点P平分∠AOB角平分线的性质定理:角平分线上的点到这个角的两边的距离相等.?
角平分线的判定定理:在一个角的内部,且到角两边距离相等的点,在这个角的平分线上思考:大家观察角平分线的性质定理与判定定理之间有什么?互逆关系例题讲练:例1. 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,
DE⊥AB于点E,点F在AC上,BD=DF.
求证:(1)CF=EB; (2)AB=AF+2EB.证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC.
在Rt△DCF和Rt△DEB中,
∴ Rt△DCF≌Rt△DEB(HL). ∴ CF=EB.
例题讲练:例题讲练:例2. 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.求证:AD是△ABC的角平分线.证明:∵DE⊥AB,DF⊥AC,
∴△BDE和△CDF是直角三角形.
∵BD=DC,BE=CF,
∴Rt△BDE≌Rt △CDF(HL).
∴DE=DF.
又∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.随堂练习:练习. 已知:如图,OC是∠AOB的平分线,点P在OC上,
PD⊥OA,PE⊥OB,垂足分别为D、E.
求证:PD=PE.证明:∵∠1=∠2,OP=OP,∠PDO=∠PEO=90°,
∴△PDO≌△PEO(AAS).
∴PD=PE(全等三角形的对应边相等).1.已知:在△AOB内部有一点P,且PD上OA,PE⊥OB,D、E为垂足且PD=PE,
求证:点P在△AOB的角平分线上. 证明:PD⊥OA,PE⊥OB,
∴∠PDO=∠ PEO=90°.
在Rt△ODP和Rt△OEP中
OP=OP,PD=PE,∴Rt△ODP ≌ Rt△OEP(HL定理).
∴∠1=∠2(全等三角形对应角相等).2.如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求 DE 的长.
?归纳小结:1.角平分线的性质定理:
角平分线上的点到这个角的两边的距离相等.?
2.角平分线的判定定理:
在一个角的内部,且到角两边距离相等的点,在这个角的平分线上.
第四节 角平分线
第2课时
北师大数学八年级下册第一章 三角形的证明
上一节课我们一起学习了角平分线的性质定理与判定定理,大家还记得这两个互逆的定理吗?请在脑海里回顾一下它们的文字语言、图形语言和几何语言.这一节课我们将学习三角形三个内角的角平分线的性质定理,并要运用三角形三条内角的角平分线的性质来解决实际问题.1.三角形三条角平分线的性质定理:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.?几何语言:∵点P是△ABC的三条角平分线的交点,且PE⊥BC,PF⊥AC,PD⊥AB,
∴PD=PE=PF. 请作出下面3个三角形的每个内角的角平分线.通过作图,大家发现了什么?2.三角形三个内角平分线的交点只有一个,实际作图时,只需作出两个角的平分线,第三个角的平分线必过这两条角平分线的交点.思考:前面我们学习了三角形各边的中垂线的性质,你能把三角形的内角平分线性质和三角形中垂线性进行一下比较吗?3.利用面积法求距离的方法:三角形角平分线的交点与三个顶点的连线,把原三角形分割成了三个小三角形,利用小三角形的面积之和等于原三角形的面积,是求角平分线交点到三边距离的常用方法.例题讲练:例1. 如图,在△ABC中,E是∠BAC,∠CBD的平分线的交点.
求证:点E在外角∠BCF的平分线上.证明:过点E作EG⊥AB,EH⊥BC,EP⊥AC,垂足分别为G, H, P.
∵AE平分∠BAC,
EG⊥AB,EP⊥AC,
∴EG=EP.
∵BE平分∠CBG,EG⊥AB,EH⊥BC,
∴EG=EH.
∴EH=EP,
又∵EP⊥AC,EH⊥BC,
∴点E在∠BCF的平分线上.例题讲练:例2. 如图,在等腰直角△ABC中,∠C=90°,AC=BC,AD平分∠BAC,DE⊥AB于E.
(1)求证:BD+DE=AC;
(2)已知AB=15 cm,求△DBE的周长;
(3)已知AC=4 cm,求CD的长.(1)证明:∵AD平分∠BAC,DE⊥AB,∠C=90°, ∴CD=DE.
∵BC=BD+CD, ∴BC=BD+DE.
∵AC=BC, ∴AC=BD+DE.例题讲练:(2)解:∵CD=DE,AD=AD,∠C= ∠AED=90°,
∴Rt△ACD≌ Rt△AED(HL), ∴AC=AE.
∵AC=BD+DE,∴BD+DE=AE.
∴△BDE的周长=BD+DE+BE=AE+BE=AB=15(cm).随堂练习:练习1. 如图,在△ABC中.AC=BC,∠C=90°,AD是△ABC的角
平分线,DE⊥AB,垂足为E.(1)已知CD=4 cm,求AC的长;
(2)求证:AB=AC+CD.【分析】本例需要运用前面所学的多个定理,而且将计算和证明融合在一起,目的是使学生进一步理解、掌握这些知识和方法,并能综合运用它们解决问题.(1)中,求AC的长,需求出BC的长,而BC=CD+DB,CD=4 cm,而BD在等腰直角三角形DBE中,根据角平分线的性质,DE=CD=4cm,再根据勾股定理便可求出DB的长.(2)中,求证AB=AC+CD.利用转化的思想AB=AE+BE,所以需证AC=AE,CD=BE.(1)解:∵AD是△ABC的角平分线,∠C=90°,DE⊥AB.
∴DE=CD=4cm(角平分线上的点到这个角两边的距离相等).
∵∠AC=∠BC ∴∠B=∠BAC(等边对等角).∵∠C=90°,∴∠B=×90°=45°.∴∠BDE=90°—45°=45°.
∴BE=DE(等角对等边).
在等腰直角三角形BDE中,BD=2DE2.=4 2 cm(勾股定理),
∴AC=BC=CD+BD=(4+42)cm.
(2)证明:由(1)的求解过程可知,Rt△ACD≌Rt△AED(HL定理)
∴AC=AE.
∵BE=DE=CD,∴AB=AE+BE=AC+CD.1.已知:如图,P是△AOB平分线上的一点,PC⊥OA,PD⊥OB,垂足分别为C、D.求证:(1)OC=OD;(2)OP是CD的垂直平分线. 证明:(1)P是∠AOB角平分线上的一点,PC⊥OA,PD⊥OB,
∴PC=PD(角平分线上的点到角两边的距离相等).
在Rt△OPC和Rt△OPD中,OP=OP,PC=PD,
∴Rt△OPC≌Rt△OPD(HL定理).
∴OC=OD(全等三角形对应边相等).
(2)又OP是∠AOB的角平分线,
∴OP是CD的垂直平分线(等腰三角形“三线合一”定理).2.如图,∠AOQ=35°,QC⊥OA于C,QD⊥OB于D,
若QC=QD,则∠AOB= °.
证明:∵QC⊥OA于C,QD⊥OB于D,QC=QD
∴ OQ是∠AOB的平分线,
∵∠AOQ=35°,
∴∠AOB=2∠AOQ=70°
故答案为70.归纳小结:1.三角形三条角平分线的性质定理:三角形的三条角平分线相交于一点,并且这一点到 三条边 的距离相等.?
2.三角形三个内角平分线的交点只有一个,实际作图时,只需作出两个角的平分线,第三个角的平分线必过这两条角平分线的交点.
3.利用面积法求距离的方法:三角形角平分线的交点与三个顶点的连线,把原三角形分割成了三个小三角形,利用小三角形的面积之和等于原三角形的面积,是求角平分线交点到三边距离的常用方法. 感谢聆听,延迟开学不停学,加油,同学们!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
