苏科版八年级下册 数学第九章 中心对称图形—平行四边形易错题整理(Word版含答案)
文档属性
| 名称 | 苏科版八年级下册 数学第九章 中心对称图形—平行四边形易错题整理(Word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 134.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-15 00:00:00 | ||
图片预览

文档简介
平行四边形易错题整理
一、填空题
1、如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,连接CE,则∠BCE的度数是_______。
2、在?ABCD中,已知DE平分∠ADC交BC边于点E,分BC为3和4两部分,则?ABCD的周长为______________。
3、已知平行四边形的三个顶点坐标分别为(0,0)、(1,4)、(3,1),则第四个顶点的坐标为___________________________________。
4、?ABCD的一组邻边长为2cm和3cm,设它的一条对角线长为xcm,则x的取值范围为______________。
5、已知平行四边形的面积是144cm2,相邻两边上的高分别为8cm和9cm,则这个平行四边
形的周长为_____________。
6、若平行四边形相邻两边的长分别是12cm和8cm,较长两边间的距离为4cm,则较短两边间的距离为_____________。
7、如图,?ABCD中,点E在边AD上,以BE为折痕将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为8,△FCB 的周长为22,则FC的长为_____________。
第1题 第7题 第8 题
8、如图,正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为______________。
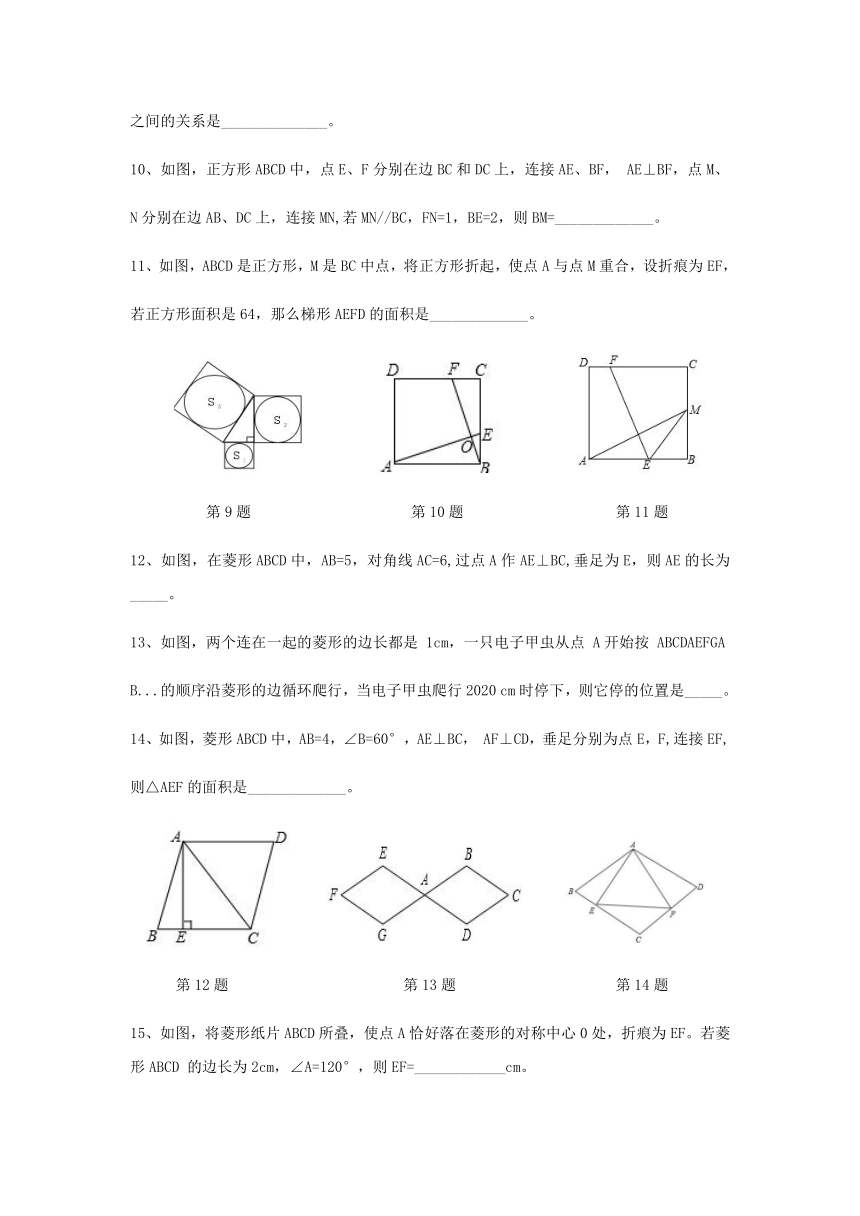
9、如图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为
圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为S1,S2,S3,则S1,S2,S3之间的关系是______________。
10、如图,正方形ABCD中,点E、F分别在边BC和DC上,连接AE、BF, AE⊥BF,点M、
N分别在边AB、DC上,连接MN,若MN//BC,FN=1,BE=2,则BM=_____________。
11、如图,ABCD是正方形,M是BC中点,将正方形折起,使点A与点M重合,设折痕为EF,
若正方形面积是64,那么梯形AEFD的面积是_____________。
第9题 第10题 第11题
12、如图,在菱形ABCD中,AB=5,对角线AC=6,过点A作AE⊥BC,垂足为E,则AE的长为_____。
13、如图,两个连在一起的菱形的边长都是 1cm,一只电子甲虫从点 A开始按 ABCDAEFGA
B...的顺序沿菱形的边循环爬行,当电子甲虫爬行2020 cm时停下,则它停的位置是_____。
14、如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC, AF⊥CD,垂足分别为点E,F,连接EF,
则△AEF的面积是_____________。
第12题 第13题 第14题
15、如图,将菱形纸片ABCD所叠,使点A恰好落在菱形的对称中心0处,折痕为EF。若菱形ABCD 的边长为2cm,∠A=120°,则EF=____________cm。
16、如果菱形的两条对角线的长为a和b,且a、b满足(a-1)2+=0,那么菱形的面积等于____________。
17、已知矩形ABCD中,对角线AC、BD相交于点0,且OE⊥BC于E,0F⊥AB于F,若0E-0F=2,
矩形的周长等于36,则矩形的面积为____________。
18、如图,把两个完全相同的矩形拼成“L”形图案,则∠FAC=_______,∠FCA=________。
19、如图,矩形ABCD中,AB=3,BC=4,BE⊥AC于E。则BE的长是____________。
20、矩形一个角的平分线分矩形的一边为1cm和3cm两部分,则这个矩形的面积为_____cm2。
第15题 第18题 第19题
21、在?ABCD中,对角线AC、BD相交于点0,如果AC=14,BD=8,AB=X,那么x的取值范围是_______________。
22、在?ABCD中,BC=3cm,∠C与∠D的平分线分别交AB于E、F,EF=2cm,则AB=_________。
23、如图,E、F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是_______________。
第23题
二、解答题
24、在直角坐标系中,直线y = - x + 4与x轴、y轴分别交于点A和点B。
(1)直接写出点A和点B的坐标;
(2) 直线y = x与直线y = - x + 4交于点P。
①求点P的坐标;
②若以P、0、A、 Q为顶点的四边形是平行四边形,直接写出第四个顶点Q的坐标。
25、动手操作:在一张长12cm、 宽5cm的矩形纸片内,要折出一个菱形。小颖同学按照取
两组对边中点的方法折出菱形EFGH (见方案一) ,小明同学沿矩形的对角线AC折出∠CA
E= ∠CAD,∠ACF= ∠ACB的方法得到菱形AECF (见方案二) 。
(1)你能说出小颖、小明所折出的菱形的理由吗?
(2)请你通过计算,比较小颖和小明同学的折法中,哪种菱形面积较大?
参考答案
一、填空题
1、22.5° 2、20或22 3、(4,5),(- 2,3),(2,- 3) 4、1 <X<5
5、 68㎝ 6、6㎝ 7、7 8 、10
9、S3=S1+S2 10、1或3 11、24 12、
13、点A 14、3 15、 16、2
17、77 18、90°, 45° 19、2.4 20、4或12
21、3 <X< 11 22、4㎝或8㎝ 23、8
2、解答题
24、(1)答:A(4,0)B(0,4).
(2)①根据题意得:y=x①,y=-x+4②
把①代入②得:x=-x+4,
解得:x=2,
∴y=x=2, ∴P(2,2)
②答:第四个顶点Q的坐标为:Q(6,2)或Q(-2,2)或Q(2,-2).
25、(1)小颖的理由:依次连接矩形各边的中点所得到的四边形是菱形,小明的理由:∵ABCD是矩形,∴AD∥BC,则∠DAC=∠ACB,又∵∠CAE=∠CAD,∠ACF=∠ACB,∴∠CAE=∠CAD=∠ACF=∠ACB,∴AE=EC=CF=FA,∴四边形AECF是菱形。
(2)方案一:S菱形=12EG?FH=12×12×5=30(cm2),方案二:设AE=EC=x则BE=12-x在Rt△ABE中,由勾股定理,得AB2+BE2=AE2,52+(12-x)2=x2,解得:x=.S菱形=EC?AB=×5≈35.21(cm2).∵30<35.21,∴小明折的菱形面积大。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
