5.1.1 相交线教学课件
图片预览



文档简介
课件18张PPT。2020年春 人教版 七年级下数学 教学课件 5.1.1 相交线1.理解邻补角与对顶角的概念; (重点)
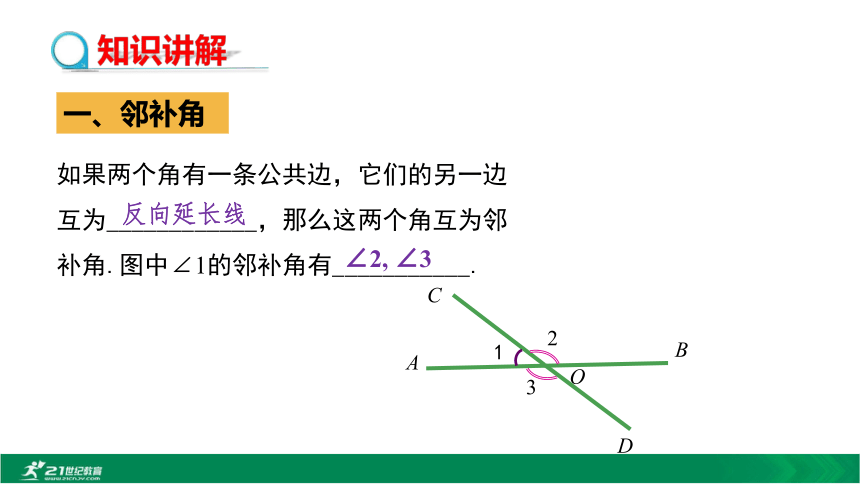
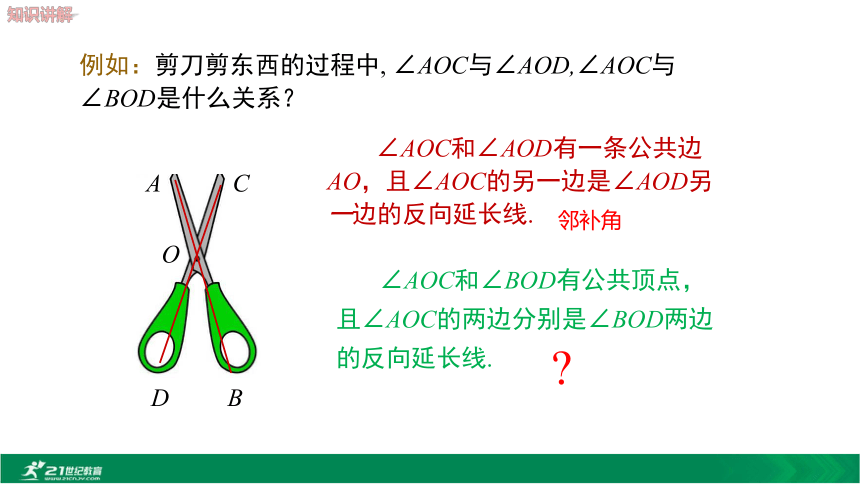
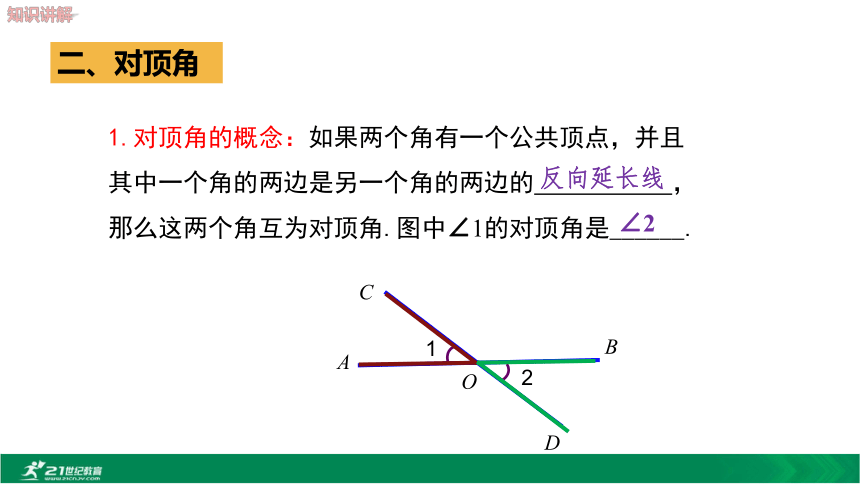
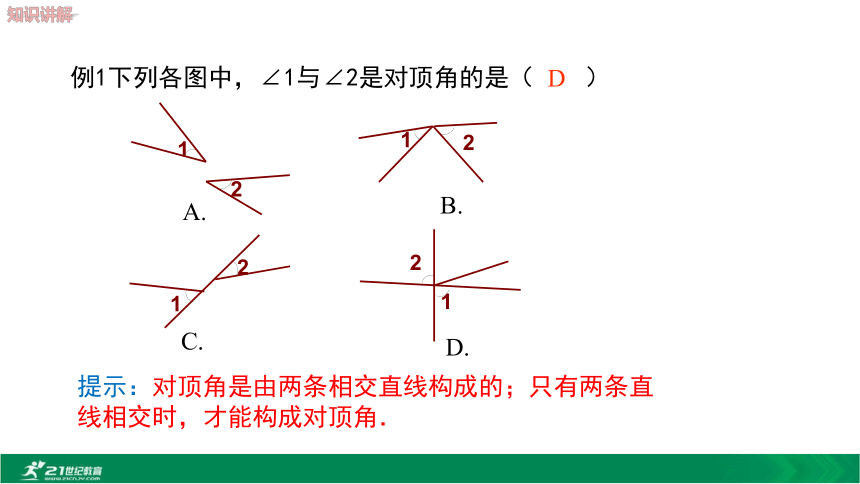
2.掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单实际问题.(难点)观察下列图片,说一说直线与直线的位置关系.一、邻补角123ABCDO如果两个角有一条公共边,它们的另一边互为____________,那么这两个角互为邻补角.图中∠1的邻补角有___________.反向延长线∠2, ∠3例如:剪刀剪东西的过程中, ∠AOC与∠AOD,∠AOC与∠BOD是什么关系?AOCBD ∠AOC和∠BOD有公共顶点,且∠AOC的两边分别是∠BOD两边的反向延长线. ∠AOC和∠AOD有一条公共边AO,且∠AOC的另一边是∠AOD另一边的反向延长线.?邻补角二、对顶角12ABCDO1.对顶角的概念:如果两个角有一个公共顶点,并且其中一个角的两边是另一个角的两边的 ,那么这两个角互为对顶角.图中∠1的对顶角是______.反向延长线∠2 例1下列各图中,∠1与∠2是对顶角的是( )D提示:对顶角是由两条相交直线构成的;只有两条直线相交时,才能构成对顶角.2.对顶角的性质:猜想:对顶角相等问题:∠1 与∠3在数量上有什么关系呢?思考:怎样说明∠1=∠3?OABCD例1如图,已知:直线AB与CD相交于点O,试说明:∠1=∠3, ∠2=∠4. 解:因为直线AB与CD相交于O点,
所以∠1+∠2=180°
∠2+∠3=180°,
所以∠1=∠3.
同理可得∠2=∠4.想一想:下图中是对顶角量角器,你能说出用它测量角的度数的原理吗?对顶角相等解:由邻补角的定义,得
∠2=180°-∠1=140°;
由对顶角相等,得
∠3=∠1=40°,
∠4= ∠2=140°.
例2如图,直线a,b相交,∠1=40°,求 ∠2,∠3,∠4 的度数.?C2.如图,直线AB与CD相交于点O,已知∠BOD=30°,OE是∠BOC的平分线,则∠EOA= .
105°3.如图,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.?4.如图,已知直线AB、CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD∶∠BOC=1∶5,求∠AOE的度数.
解:(1)∠BOE=180°-∠AOC-∠COE=180°-36°-90°=54°.
(2)因为∠BOD∶∠BOC=1∶5,∠BOD+∠BOC=180°,
所以∠BOD=30°.
因为∠AOC=∠BOD,
所以∠AOC=30°,
所以∠AOE=∠COE+∠AOC=90°+30°=120°.
5. 观察下列各图,寻找对顶角(不含平角) ⑴ 如图1,图中共有 对对顶角;
⑵ 如图2,图中共有 对对顶角;
⑶ 如图3,图中共有 对对顶角;
⑷ 研究⑴~⑶小题中直线条数与对顶角的对数之间的
关系,猜测:若有n条直线相交于一点,则可形成
对对顶角;
⑸ 若有20条直线相交于一点,则可形成 对对顶角.图1图2图32612n(n-1)380对顶
角相
等
邻补
角互
补 ②有公共顶点;③有一条公共边①两条直线相交形成的角; ①两条直线相交而成的角;②有公共顶点;③没有公共边①都是两条直线相交而成的角;③都是成对出现的 ②都有一个公共顶点;②两直线相交时,对顶角只有两对,邻补角有四对 ①有无公共边;谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
2.掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单实际问题.(难点)观察下列图片,说一说直线与直线的位置关系.一、邻补角123ABCDO如果两个角有一条公共边,它们的另一边互为____________,那么这两个角互为邻补角.图中∠1的邻补角有___________.反向延长线∠2, ∠3例如:剪刀剪东西的过程中, ∠AOC与∠AOD,∠AOC与∠BOD是什么关系?AOCBD ∠AOC和∠BOD有公共顶点,且∠AOC的两边分别是∠BOD两边的反向延长线. ∠AOC和∠AOD有一条公共边AO,且∠AOC的另一边是∠AOD另一边的反向延长线.?邻补角二、对顶角12ABCDO1.对顶角的概念:如果两个角有一个公共顶点,并且其中一个角的两边是另一个角的两边的 ,那么这两个角互为对顶角.图中∠1的对顶角是______.反向延长线∠2 例1下列各图中,∠1与∠2是对顶角的是( )D提示:对顶角是由两条相交直线构成的;只有两条直线相交时,才能构成对顶角.2.对顶角的性质:猜想:对顶角相等问题:∠1 与∠3在数量上有什么关系呢?思考:怎样说明∠1=∠3?OABCD例1如图,已知:直线AB与CD相交于点O,试说明:∠1=∠3, ∠2=∠4. 解:因为直线AB与CD相交于O点,
所以∠1+∠2=180°
∠2+∠3=180°,
所以∠1=∠3.
同理可得∠2=∠4.想一想:下图中是对顶角量角器,你能说出用它测量角的度数的原理吗?对顶角相等解:由邻补角的定义,得
∠2=180°-∠1=140°;
由对顶角相等,得
∠3=∠1=40°,
∠4= ∠2=140°.
例2如图,直线a,b相交,∠1=40°,求 ∠2,∠3,∠4 的度数.?C2.如图,直线AB与CD相交于点O,已知∠BOD=30°,OE是∠BOC的平分线,则∠EOA= .
105°3.如图,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.?4.如图,已知直线AB、CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD∶∠BOC=1∶5,求∠AOE的度数.
解:(1)∠BOE=180°-∠AOC-∠COE=180°-36°-90°=54°.
(2)因为∠BOD∶∠BOC=1∶5,∠BOD+∠BOC=180°,
所以∠BOD=30°.
因为∠AOC=∠BOD,
所以∠AOC=30°,
所以∠AOE=∠COE+∠AOC=90°+30°=120°.
5. 观察下列各图,寻找对顶角(不含平角) ⑴ 如图1,图中共有 对对顶角;
⑵ 如图2,图中共有 对对顶角;
⑶ 如图3,图中共有 对对顶角;
⑷ 研究⑴~⑶小题中直线条数与对顶角的对数之间的
关系,猜测:若有n条直线相交于一点,则可形成
对对顶角;
⑸ 若有20条直线相交于一点,则可形成 对对顶角.图1图2图32612n(n-1)380对顶
角相
等
邻补
角互
补 ②有公共顶点;③有一条公共边①两条直线相交形成的角; ①两条直线相交而成的角;②有公共顶点;③没有公共边①都是两条直线相交而成的角;③都是成对出现的 ②都有一个公共顶点;②两直线相交时,对顶角只有两对,邻补角有四对 ①有无公共边;谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
