5.3.1 第1课时平行线的性质教学课件
图片预览




文档简介
课件18张PPT。2020年春 人教版 七年级下数学 教学课件 5.3.1 第1 课时 平行线的性质1.掌握平行线的性质,会运用平行线的性质判
断角相等或互补;(重点)
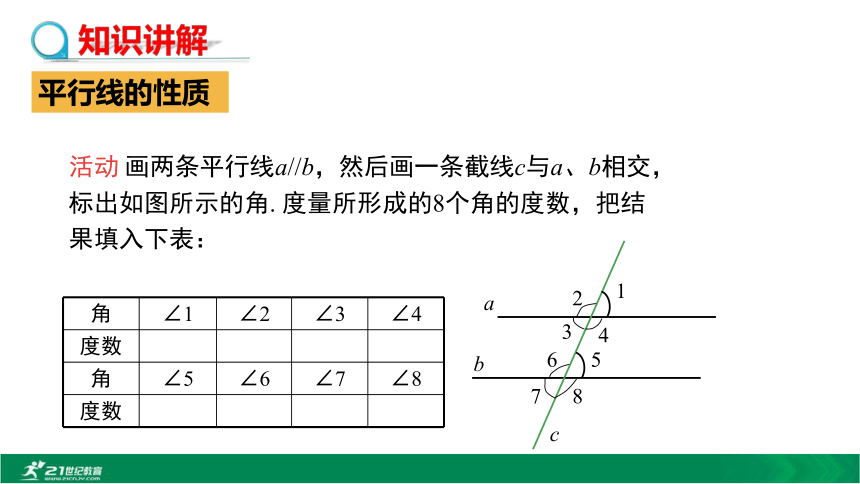
2.能够根据平行线的性质进行简单的推理. 问题 平行线的判定方法是什么?思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?平行线的性质活动 画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:观察 ∠1~ ∠8中,哪些是同位角?它们的度数
之间有什么关系?说出你的猜想: 性质1:两条平行线被第三条直线所截,
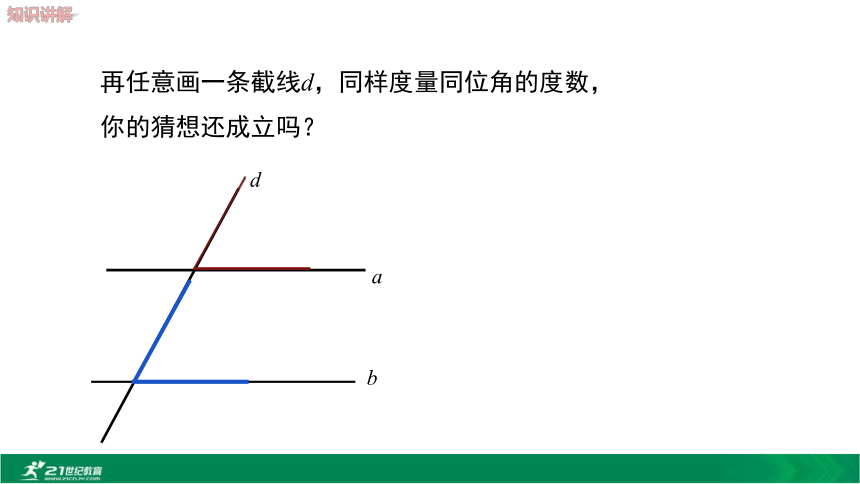
同位角___.相等简单说成:两直线平行,同位角相等.∴∠1=∠5 (两直线平行,同位角相等).∵a∥b(已知),应用格式:abd再任意画一条截线d,同样度量同位角的度数,你的猜想还成立吗? 如图,已知a//b,那么?2与?3相等吗?为什么?解 :∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等. ∴∠2=∠3
(两直线平行,内错角相等).∵a∥b(已知),应用格式:如图,已知a//b,那么?2与?4有什么关系呢?为什么?解: ∵a//b (已知), ∴? 1= ? 2
(两直线平行,同位角相等). ∵ ? 1+ ? 4=180° (邻补角的性质), ∴? 2+ ? 4=180° (等量代换).思考:类似地,已知两直线平行,能否得到同旁内角之间的数量关系? 性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补. ∴∠2+∠4=180 °
(两直线平行,同旁内角互补).∵a∥b(已知),应用格式:例 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?解:因为梯形上、下底互相平行,
根据“两直线平行,同旁内角互补”
可得∠A与∠D互补, ∠B与∠C互补.所以梯形的另外两个角分别是80°、65°.于是∠D=180 °-∠A=180°-100°=80°,
∠C= 180 °-∠B=180°-115°=65°.1.如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4
C.∠1+∠3=180°
D.∠3+∠4=180°
2.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )
A.14° B.15°
C.16° D.17°
DC3.如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠CED的度数为 .4.如图,直线 a ∥ b,直线b垂直于直线c,那么直线a垂直于直线c吗? 解:a⊥c .
因为两直线平行, 同位角相等 60°5.如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度吗,为什么?
(2)从∠1=110o可以知道 ∠3是多少度吗,为什么?
(3)从 ∠1=110o可以知道∠4 是多少度吗,为什么?解:(1)∠2=110o
∵两直线平行,内错角相等;(2)∠3=110o
∵两直线平行, 同位角相等;(3)∠4=70o
∵两直线平行,同旁内角互补.6.如图,AB∥CD,DE⊥AC,垂足为点E,∠A=105°,求∠D的度数.解:∵AB∥CD,
∴∠A+∠C=180°(两直线平行,同旁内角互补).
∵∠A=105°,
∴∠C=180°-105°=75°.
又∵DE⊥AC,
∴∠DEC=90°,
∴∠C+∠D=90°.
∴∠D=90°-75°=15°.
两直线平行 同位角相等内错角相等同旁内角互补平行线的判定平行线的性质直线的位置关系角的数量关系性质角的数量关系直线的位置关系判定谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
断角相等或互补;(重点)
2.能够根据平行线的性质进行简单的推理. 问题 平行线的判定方法是什么?思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?平行线的性质活动 画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:观察 ∠1~ ∠8中,哪些是同位角?它们的度数
之间有什么关系?说出你的猜想: 性质1:两条平行线被第三条直线所截,
同位角___.相等简单说成:两直线平行,同位角相等.∴∠1=∠5 (两直线平行,同位角相等).∵a∥b(已知),应用格式:abd再任意画一条截线d,同样度量同位角的度数,你的猜想还成立吗? 如图,已知a//b,那么?2与?3相等吗?为什么?解 :∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等. ∴∠2=∠3
(两直线平行,内错角相等).∵a∥b(已知),应用格式:如图,已知a//b,那么?2与?4有什么关系呢?为什么?解: ∵a//b (已知), ∴? 1= ? 2
(两直线平行,同位角相等). ∵ ? 1+ ? 4=180° (邻补角的性质), ∴? 2+ ? 4=180° (等量代换).思考:类似地,已知两直线平行,能否得到同旁内角之间的数量关系? 性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补. ∴∠2+∠4=180 °
(两直线平行,同旁内角互补).∵a∥b(已知),应用格式:例 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?解:因为梯形上、下底互相平行,
根据“两直线平行,同旁内角互补”
可得∠A与∠D互补, ∠B与∠C互补.所以梯形的另外两个角分别是80°、65°.于是∠D=180 °-∠A=180°-100°=80°,
∠C= 180 °-∠B=180°-115°=65°.1.如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4
C.∠1+∠3=180°
D.∠3+∠4=180°
2.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )
A.14° B.15°
C.16° D.17°
DC3.如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠CED的度数为 .4.如图,直线 a ∥ b,直线b垂直于直线c,那么直线a垂直于直线c吗? 解:a⊥c .
因为两直线平行, 同位角相等 60°5.如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度吗,为什么?
(2)从∠1=110o可以知道 ∠3是多少度吗,为什么?
(3)从 ∠1=110o可以知道∠4 是多少度吗,为什么?解:(1)∠2=110o
∵两直线平行,内错角相等;(2)∠3=110o
∵两直线平行, 同位角相等;(3)∠4=70o
∵两直线平行,同旁内角互补.6.如图,AB∥CD,DE⊥AC,垂足为点E,∠A=105°,求∠D的度数.解:∵AB∥CD,
∴∠A+∠C=180°(两直线平行,同旁内角互补).
∵∠A=105°,
∴∠C=180°-105°=75°.
又∵DE⊥AC,
∴∠DEC=90°,
∴∠C+∠D=90°.
∴∠D=90°-75°=15°.
两直线平行 同位角相等内错角相等同旁内角互补平行线的判定平行线的性质直线的位置关系角的数量关系性质角的数量关系直线的位置关系判定谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
