6.3.1 实数教学课件
图片预览







文档简介
课件23张PPT。2020年春 人教版 七年级下数学 教学课件 6.3 第1 课时 实数探究我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?它们都可以化成有限小数或无限循环小数的形式???思考1:(1)整数能写成小数的形式吗?3可以看成是3.0吗?可以(2)由此你可以得到什么结论?任何一个有理数都可以写成有限小数或无限循环小数;反过来,任何有限小数或无限循环小数也都是有理数.思考2:除了有限小数和无限循环小数,还有什么其他类
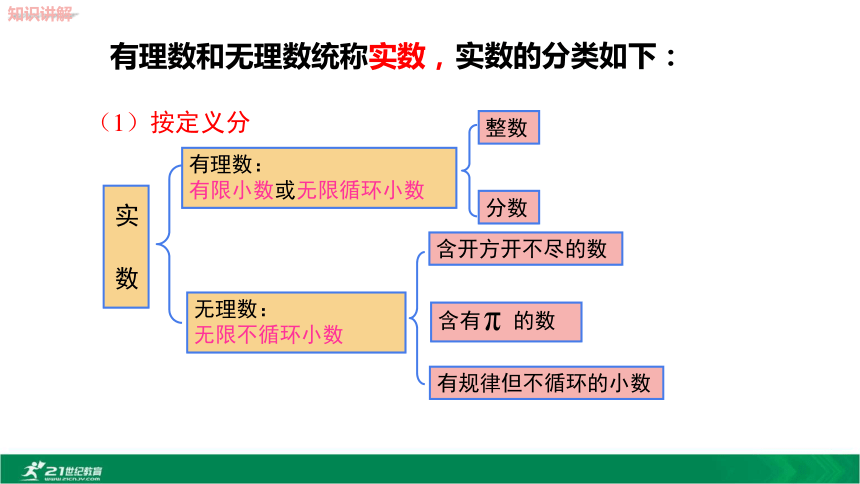
型的小数吗?无限不循环小数叫做无理数???把下列各数分别填入相应的集合内:0.101, 有理数集合 无理数集合?(相邻两个3之间7的个数逐渐加1)有理数和无理数统称实数,无理数:
无限不循环小数有理数:
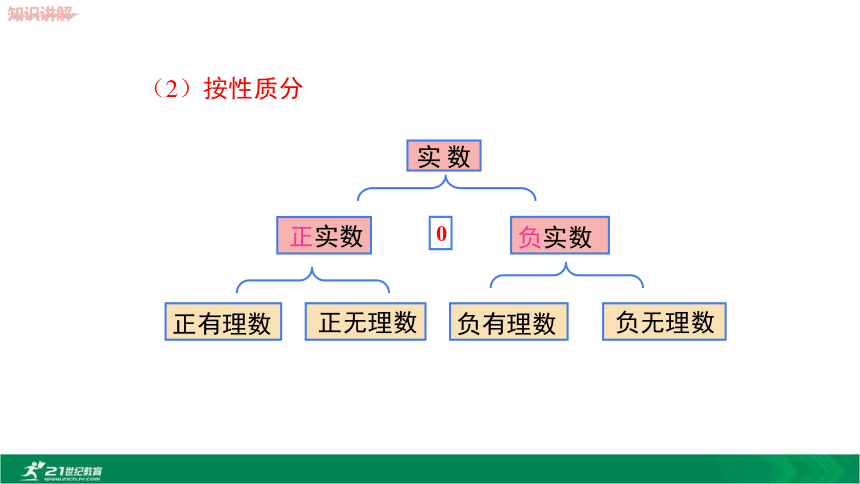
有限小数或无限循环小数实 数(1)按定义分分数整数含开方开不尽的数有规律但不循环的小数实数的分类如下:负实数 正实数数实正有理数负有理数(2)按性质分0 正无理数 负无理数判断:1.实数不是有理数就是无理数.( )2.无理数都是无限不循环小数.( )3.无理数都是无限小数.( )4.带根号的数都是无理数.( )5.无理数一定都带根号.( )6.两个无理数之积不一定是无理数.( )7.两个无理数之和一定是无理数.( )××× 有理数:负实数:正实数: 将下列各数分别填入下列相应的括号内:每个有理数都可以用数轴上的点表示,那么无理数 是否也可以用数轴上的点来表示呢??直径为1的圆1111?每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.★实数和数轴上的点是一一对应的. 如图所示,数轴上A,B两点表示的数分别为
和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个?C 与有理数一样,实数也可以比较大小:同样的,数轴上右边的点表示的实数比左边的点表示的实数大.<1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.与有理数一样,在实数范围内:?1-2?????B2.估计 位于( )A.0~1之间 B.1~2之间
C.2~3之间 D.3~4之间B3.把下列各数填入相应的集合内:(1)有理数集合:(2)无理数集合:(3)整数集合:(4)分数集合:(5)正实数数集合:(6)负实数集合:(7) 实数集合:???????解:?????无限不循环小数叫做无理数;有理数与无理数统称实数.2. 实数的分类1. 无理数及实数的概念无理数:
无限不循环小数有理数:
有限小数或无限循环小数实 数(1)按定义分分数整数含开方开不尽的数有规律但不循环的小数负实数 正实数数实正有理数负有理数(2)按性质分0 正无理数 负无理数3.常见的一些无理数:?谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
型的小数吗?无限不循环小数叫做无理数???把下列各数分别填入相应的集合内:0.101, 有理数集合 无理数集合?(相邻两个3之间7的个数逐渐加1)有理数和无理数统称实数,无理数:
无限不循环小数有理数:
有限小数或无限循环小数实 数(1)按定义分分数整数含开方开不尽的数有规律但不循环的小数实数的分类如下:负实数 正实数数实正有理数负有理数(2)按性质分0 正无理数 负无理数判断:1.实数不是有理数就是无理数.( )2.无理数都是无限不循环小数.( )3.无理数都是无限小数.( )4.带根号的数都是无理数.( )5.无理数一定都带根号.( )6.两个无理数之积不一定是无理数.( )7.两个无理数之和一定是无理数.( )××× 有理数:负实数:正实数: 将下列各数分别填入下列相应的括号内:每个有理数都可以用数轴上的点表示,那么无理数 是否也可以用数轴上的点来表示呢??直径为1的圆1111?每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.★实数和数轴上的点是一一对应的. 如图所示,数轴上A,B两点表示的数分别为
和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个?C 与有理数一样,实数也可以比较大小:同样的,数轴上右边的点表示的实数比左边的点表示的实数大.<1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.与有理数一样,在实数范围内:?1-2?????B2.估计 位于( )A.0~1之间 B.1~2之间
C.2~3之间 D.3~4之间B3.把下列各数填入相应的集合内:(1)有理数集合:(2)无理数集合:(3)整数集合:(4)分数集合:(5)正实数数集合:(6)负实数集合:(7) 实数集合:???????解:?????无限不循环小数叫做无理数;有理数与无理数统称实数.2. 实数的分类1. 无理数及实数的概念无理数:
无限不循环小数有理数:
有限小数或无限循环小数实 数(1)按定义分分数整数含开方开不尽的数有规律但不循环的小数负实数 正实数数实正有理数负有理数(2)按性质分0 正无理数 负无理数3.常见的一些无理数:?谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
