人教版八年级数学下册:19.1.1《变量与函数》课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学下册:19.1.1《变量与函数》课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 22:22:10 | ||
图片预览






文档简介
(共18张PPT)
19.1.1
变量与函数
在一个变化过程中,我们称
( )为变量,
( )为常量。
研究什么?
怎么研究?
数值发生变化的量
数值始终不变的量
两个变量之间的关系
从具体问题出发
导入
例1:阳泉曲到太原的火车以80km/h的速度在轨道上匀速行驶,行驶路程为s km,行驶时间为t h。
有哪些量?
这些量满足什么关系式?
变量是什么?
两个变量之间有什么关系?
s=80t
形成概念
例1:阳泉曲到太原的火车以80km/h的速度在轨道上匀速行驶,行驶路程为s km,行驶时间为t h。
当 t=1时,
s=80;
当 t=2时,
s=160;
当 t=2.5时,能求出s的值吗?能求出几个?
当 t=2.6、2.7时,能求出s的值吗?都是只能求出一个吗?
s=80t
形成概念
例2:沃尔玛销售某种商品,已知该商品进价40元/件,商场工作人员记录了该商品在8天中按不同售价出售时每天所获得的利润,具体数值如下表:
这是一个变化过程吗?在这个变化过程中包含那些量?哪些是变量?两个变量之间是否有上题所总结的关系。
形成概念
售价
x(元/件) 60 61 62 63 64 65 66 67
利润y(元) 6000 6090 6160 6210 6240 6250 6240 6210
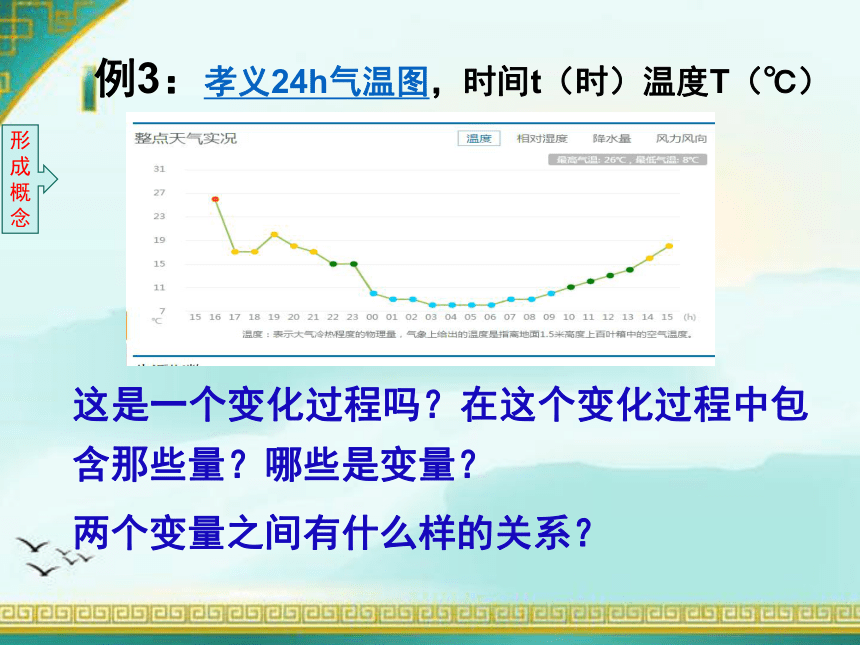
例3:孝义24h气温图,时间t(时)温度T(℃)
这是一个变化过程吗?在这个变化过程中包含那些量?哪些是变量?
两个变量之间有什么样的关系?
形成概念
结合3个实际问题,思考:
每个问题都是一个变化过程吗?在这个变化过程中包含那些量?哪些是变量?每个问题中有几个变量?两个变量之间是否具有相同的关系?如果有,这个相同关系是什么?
归纳上述这些具体问题的共性,就可以得到一个非常重要的数学概念——函数。能说说归纳的结果吗?
形成概念
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,我们就说x是自变量,y是x的函数.
如果当x=a时,y=b,
那么b叫做当自变量的值为a时的函数值.
函数的概念:
结合例3,说明什么是唯一确定?
如何判断一个变量是否为另一个变量的函数?
形成概念
最早给出函数概念明确定义的是詹姆斯·格雷戈里。1667年,他的函数定义为:“它是从一些其它的量经过一系列代数运算而得到的,或者是经过任何其它可以想象的运算而得到的。”
1775年数学家欧拉又给出一个新的函数定义:如果一个变量依赖于另一个变量,使当后一个变量变化时,前一个量也随着变化,那么称第一个量是第二个量的函数。
函数概念从提出到完成,用了二百多年的时间,经历了由不全面到全面,不严密到严密的发展过程,才逐步形成了今天的函数概念。
1859年我国清代数学家李善兰翻译《代数学》一书
时首先用“函数”一词翻译“function”一词,他解释
说:“凡此变数函彼变数,则此为彼之函数”。中国古
代用天、地、人、物表示未知数。李善兰译《代数学》
中有“凡式中含天,为天之函数”这样的语句。函数思
想,是指用函数的概念和性质去分析问题、转化问题和
解决问题。
李善兰
追根溯源
课外延伸
练一练:
1.下列问题中的变量y是不是x的函数?
是
是
不是
是
不是
是
是
不是
不是
辨析概念
x任取一个值,y都有唯一确定的值与之对应
2、两个变量关系如下表,y是x的函数吗?
3、下列曲线中,表示y不是x的函数是( ),怎样改动这条曲线,才能使y是x的函数?
辨析概念
一个数的平方x 1 2 16 36 49
这个数y ±1 ±4 ±6 ±7
函数关系的表示方法:
像S=80t,y=2x,y=x2这样,用关于自变量的式子表示函数与自变量之间的关系,这种式子叫做函数的解析式。 (叫解析式法)
像气温变化图,函数关系是用图象给出的
(叫图象法)
像沃尔玛商品销售统计表,函数关系是用表格给出的 (叫列表法)
例4:汽车油箱有汽油50 L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程 x(单位:km)的增加而减少,平均油耗为0.1L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3)汽车行驶200 km时,油箱中还有多少汽油?
运用概念
例4:汽车油箱有汽油50 L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程 x(单位:km)的增加而减少,平均油耗为0.1L/km.
解:(1)关系式为:y =50-0.1x;
(2)0≤x≤500;
(3)∵当x=200时,y=50-0.1×200=30,
∴汽车行驶200 km时,油箱中还有30L汽油.
在用解析式表示函数时,自变量的取值往往有一定的范围,这个范围叫做自变量的取值范围.
①解析式本身有意义
②符合实际意义
运用概念
(1) y=3x (2) y=x2+9 ?
(3) y= (4) y=
(1)x为任意实数(或全体实数);
(3)由x-3≠0 得x≠3;
(4)由2x-8≥0得x≥4.
解:
(2) x为任意实数;
练一练 求下列函数关系式中自变量x的取值范围:?
巧记自变量的取值范围:
分式分母不为零,
偶次根下负不行;
零次幂底数不为零,
整式、奇次根全能行.
升华概念
课堂小结
谈谈本节课的收获……
总结反思
课尾检测
课本81页3,4,5,7。
巩固提升
用数学的眼光观察世界
用数学的思维分析世界
用数学的语言表达世界
19.1.1
变量与函数
在一个变化过程中,我们称
( )为变量,
( )为常量。
研究什么?
怎么研究?
数值发生变化的量
数值始终不变的量
两个变量之间的关系
从具体问题出发
导入
例1:阳泉曲到太原的火车以80km/h的速度在轨道上匀速行驶,行驶路程为s km,行驶时间为t h。
有哪些量?
这些量满足什么关系式?
变量是什么?
两个变量之间有什么关系?
s=80t
形成概念
例1:阳泉曲到太原的火车以80km/h的速度在轨道上匀速行驶,行驶路程为s km,行驶时间为t h。
当 t=1时,
s=80;
当 t=2时,
s=160;
当 t=2.5时,能求出s的值吗?能求出几个?
当 t=2.6、2.7时,能求出s的值吗?都是只能求出一个吗?
s=80t
形成概念
例2:沃尔玛销售某种商品,已知该商品进价40元/件,商场工作人员记录了该商品在8天中按不同售价出售时每天所获得的利润,具体数值如下表:
这是一个变化过程吗?在这个变化过程中包含那些量?哪些是变量?两个变量之间是否有上题所总结的关系。
形成概念
售价
x(元/件) 60 61 62 63 64 65 66 67
利润y(元) 6000 6090 6160 6210 6240 6250 6240 6210
例3:孝义24h气温图,时间t(时)温度T(℃)
这是一个变化过程吗?在这个变化过程中包含那些量?哪些是变量?
两个变量之间有什么样的关系?
形成概念
结合3个实际问题,思考:
每个问题都是一个变化过程吗?在这个变化过程中包含那些量?哪些是变量?每个问题中有几个变量?两个变量之间是否具有相同的关系?如果有,这个相同关系是什么?
归纳上述这些具体问题的共性,就可以得到一个非常重要的数学概念——函数。能说说归纳的结果吗?
形成概念
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,我们就说x是自变量,y是x的函数.
如果当x=a时,y=b,
那么b叫做当自变量的值为a时的函数值.
函数的概念:
结合例3,说明什么是唯一确定?
如何判断一个变量是否为另一个变量的函数?
形成概念
最早给出函数概念明确定义的是詹姆斯·格雷戈里。1667年,他的函数定义为:“它是从一些其它的量经过一系列代数运算而得到的,或者是经过任何其它可以想象的运算而得到的。”
1775年数学家欧拉又给出一个新的函数定义:如果一个变量依赖于另一个变量,使当后一个变量变化时,前一个量也随着变化,那么称第一个量是第二个量的函数。
函数概念从提出到完成,用了二百多年的时间,经历了由不全面到全面,不严密到严密的发展过程,才逐步形成了今天的函数概念。
1859年我国清代数学家李善兰翻译《代数学》一书
时首先用“函数”一词翻译“function”一词,他解释
说:“凡此变数函彼变数,则此为彼之函数”。中国古
代用天、地、人、物表示未知数。李善兰译《代数学》
中有“凡式中含天,为天之函数”这样的语句。函数思
想,是指用函数的概念和性质去分析问题、转化问题和
解决问题。
李善兰
追根溯源
课外延伸
练一练:
1.下列问题中的变量y是不是x的函数?
是
是
不是
是
不是
是
是
不是
不是
辨析概念
x任取一个值,y都有唯一确定的值与之对应
2、两个变量关系如下表,y是x的函数吗?
3、下列曲线中,表示y不是x的函数是( ),怎样改动这条曲线,才能使y是x的函数?
辨析概念
一个数的平方x 1 2 16 36 49
这个数y ±1 ±4 ±6 ±7
函数关系的表示方法:
像S=80t,y=2x,y=x2这样,用关于自变量的式子表示函数与自变量之间的关系,这种式子叫做函数的解析式。 (叫解析式法)
像气温变化图,函数关系是用图象给出的
(叫图象法)
像沃尔玛商品销售统计表,函数关系是用表格给出的 (叫列表法)
例4:汽车油箱有汽油50 L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程 x(单位:km)的增加而减少,平均油耗为0.1L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3)汽车行驶200 km时,油箱中还有多少汽油?
运用概念
例4:汽车油箱有汽油50 L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程 x(单位:km)的增加而减少,平均油耗为0.1L/km.
解:(1)关系式为:y =50-0.1x;
(2)0≤x≤500;
(3)∵当x=200时,y=50-0.1×200=30,
∴汽车行驶200 km时,油箱中还有30L汽油.
在用解析式表示函数时,自变量的取值往往有一定的范围,这个范围叫做自变量的取值范围.
①解析式本身有意义
②符合实际意义
运用概念
(1) y=3x (2) y=x2+9 ?
(3) y= (4) y=
(1)x为任意实数(或全体实数);
(3)由x-3≠0 得x≠3;
(4)由2x-8≥0得x≥4.
解:
(2) x为任意实数;
练一练 求下列函数关系式中自变量x的取值范围:?
巧记自变量的取值范围:
分式分母不为零,
偶次根下负不行;
零次幂底数不为零,
整式、奇次根全能行.
升华概念
课堂小结
谈谈本节课的收获……
总结反思
课尾检测
课本81页3,4,5,7。
巩固提升
用数学的眼光观察世界
用数学的思维分析世界
用数学的语言表达世界
