华师大版八年级数学下册18.2.3平行四边形的判定和性质的综合应用同步测试(含解析)
文档属性
| 名称 | 华师大版八年级数学下册18.2.3平行四边形的判定和性质的综合应用同步测试(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 466.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览


文档简介
18.2.3 平行四边形的判定与性质的综合应用
知识点 1 平行四边形判定和性质的综合应用
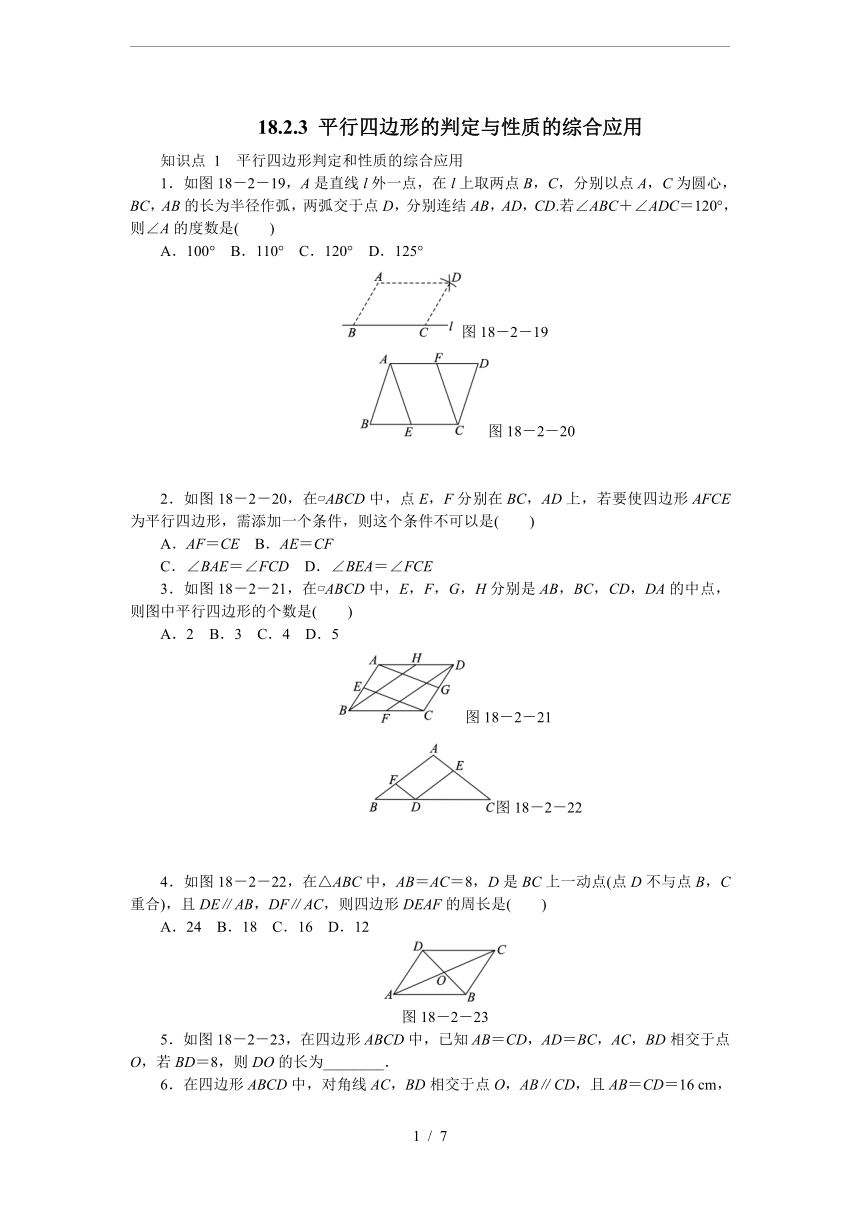
1.如图18-2-19,A是直线l外一点,在l上取两点B,C,分别以点A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连结AB,AD,CD.若∠ABC+∠ADC=120°,则∠A的度数是( )
A.100° B.110° C.120° D.125°
图18-2-19
图18-2-20
2.如图18-2-20,在?ABCD中,点E,F分别在BC,AD上,若要使四边形AFCE为平行四边形,需添加一个条件,则这个条件不可以是( )
A.AF=CE B.AE=CF
C.∠BAE=∠FCD D.∠BEA=∠FCE
3.如图18-2-21,在?ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,则图中平行四边形的个数是( )
A.2 B.3 C.4 D.5
图18-2-21
图18-2-22
4.如图18-2-22,在△ABC中,AB=AC=8,D是BC上一动点(点D不与点B,C重合),且DE∥AB,DF∥AC,则四边形DEAF的周长是( )
A.24 B.18 C.16 D.12
图18-2-23
5.如图18-2-23,在四边形ABCD中,已知AB=CD,AD=BC,AC,BD相交于点O,若BD=8,则DO的长为________.
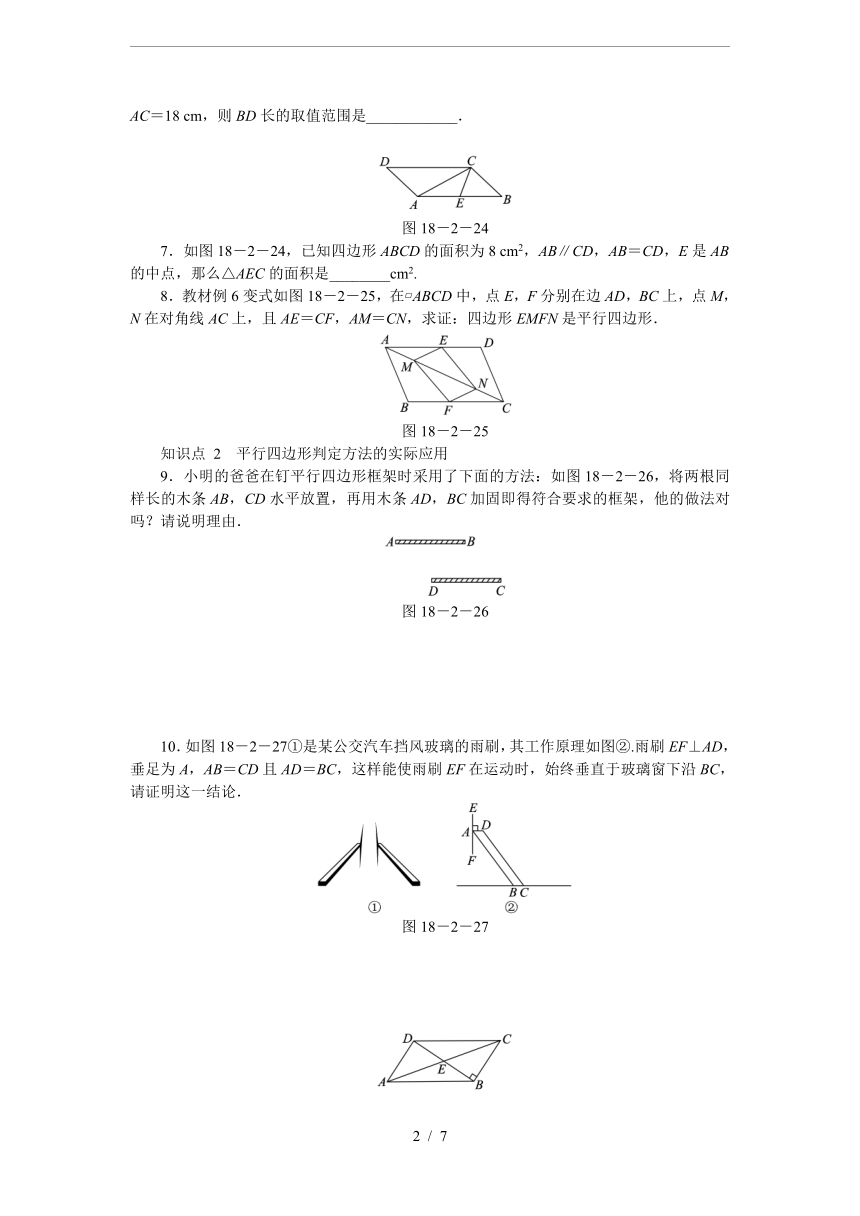
6.在四边形ABCD中,对角线AC,BD相交于点O,AB∥CD,且AB=CD=16 cm,AC=18 cm,则BD长的取值范围是____________.
图18-2-24
7.如图18-2-24,已知四边形ABCD的面积为8 cm2,AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是________cm2.
8.教材例6变式如图18-2-25,在?ABCD中,点E,F分别在边AD,BC上,点M,N在对角线AC上,且AE=CF,AM=CN,求证:四边形EMFN是平行四边形.
图18-2-25
知识点 2 平行四边形判定方法的实际应用
9.小明的爸爸在钉平行四边形框架时采用了下面的方法:如图18-2-26,将两根同样长的木条AB,CD水平放置,再用木条AD,BC加固即得符合要求的框架,他的做法对吗?请说明理由.
图18-2-26
10.如图18-2-27①是某公交汽车挡风玻璃的雨刷,其工作原理如图②.雨刷EF⊥AD,垂足为A,AB=CD且AD=BC,这样能使雨刷EF在运动时,始终垂直于玻璃窗下沿BC,请证明这一结论.
图18-2-27
图18-2-16
【能力提升】
11.在?ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3 B.5
C.2或3 D.3或5
图18-2-28
12.如图18-2-28,AE∥BD,BE∥DF,AB∥CD,现给出四个结论:(1)四边形ABDC是平行四边形;(2)BE=DF;(3)S四边形ABDC=S四边形BDFE;(4)BD=CE.其中错误的有( )
A.4个 B.3个 C.2个 D.1个
13.如图18-2-29,点A,E,F,C在一条直线上,若将△DEC的EC边沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于点E,BF⊥AC于点F,且AB=CD,则当点E,F不重合时,BD与EF的关系是____________.
图18-2-29
图18-2-30
14.如图18-2-30所示,AC是?ABCD的对角线,过对角线AC上一点M任作直线EF交DC于点E,交AB于点F,要使四边形AECF是平行四边形,则点M需满足的条件是________________.
15.2018·徐州已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC;②AB=CD;③∠BAD=∠DCB;④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)构造一个真命题,画图并给出证明;
(2)构造一个假命题,举反例加以说明.
16.如图18-2-31,在六边形ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F,且AB+BC=22,试求DE+EF的值.
图18-2-31
17.如图18-2-32,在四边形ABCD中,AD∥BC,AD=24 cm,BC=26 cm.点P从点A出发,以1 cm/s的速度向点D运动;点Q从点C同时出发,以3 cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,要使PQ∥CD,需经过多少时间?为什么?
图18-2-32
答案
1.C [解析] ∵AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,AD∥BC,
∴∠A+∠ABC=180°.
∵∠ABC+∠ADC=120°,
∴∠ABC=60°,
∴∠A=120°.
故选C.
2.B [解析] A项,∵四边形ABCD是平行四边形,
∴AF∥CE.
∵AF=CE,
∴四边形AFCE是平行四边形.
∴选项A不符合题意;
B项,根据AE=CF,可知四边形AFCE可能是平行四边形,也有可能是等腰梯形,故选项B符合题意;
C项,由∠BAE=∠FCD,AB=CD,∠B=∠D可以推出△ABE≌△CDF,∴BE=DF.
∵AD=BC,∴AF=CE.
又∵AF∥CE,
∴四边形AFCE是平行四边形.
故选项C不符合题意;
D项,∵∠BEA=∠FCE,∴AE∥CF.
又∵AF∥CE,
∴四边形AFCE是平行四边形.
故选项D不符合题意.
故选B.
3.C [解析] ∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴AE=CG,
∴四边形AECG是平行四边形,
同理:四边形BFDH是平行四边形,四边形OPMN是平行四边形.
故选C.
4.C [解析] ∵AB=AC,
∴∠B=∠C.
∵DE∥AB,
∴∠B=∠CDE,
∴∠C=∠CDE,
∴CE=DE,同理可得BF=DF,
∴四边形DEAF的周长=AF+DF+DE+AE=AF+BF+CE+AE=AB+AC.
∵AB=AC=8,∴四边形DEAF的周长=8+8=16.故选C.
5.4 [解析] ∵在四边形ABCD中,AB=CD,AD=BC,∴四边形ABCD是平行四边形.∵BD=8,∴DO=4.
6.14 cm<BD<50 cm
[解析] ∵AB∥CD,AB=CD=16 cm,
∴四边形ABCD是平行四边形,
∴OC=OA,OB=OD.
∵在△OCD中,CD=16 cm,OC=9 cm,
∴CD-OC<OD<CD+OC,
即7 cm<OD<25 cm,
∴14 cm<2OD<50 cm,
即14 cm<BD<50 cm.
故答案是14 cm<BD<50 cm.
7.2 [解析] ∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴S△ADC=S△ABC=×8=4(cm2).
∵E是AB的中点,
∴S△AEC=S△ABC=×4=2(cm2).
8.证明:∵在?ABCD中,AD∥BC,
∴∠DAC=∠BCA.
又∵AE=CF,AM=CN,∴△AEM≌△CFN,
∴EM=FN,∠AME=∠CNF,
∴∠EMN=∠FNM,∴EM∥FN,
∴四边形EMFN是平行四边形.
9.解:他的做法是对的.理由:由已知得AB与CD平行且相等,根据“一组对边平行且相等的四边形是平行四边形”可知,四边形ABCD是平行四边形.
10.证明:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AD∥BC.
又∵EF⊥AD,∴EF⊥BC.
11.D
12.D [解析] 由已知可得,四边形ABDC和四边形BDFE都是平行四边形,故(1)(2)正确;又因为四边形ABDC和四边形BDFE同底等高,所以面积相等,故(3)正确;BD=AC=EF,它们与CE不一定相等,故(4)错误.故选D.
13.互相平分
14.M是AC的中点
15.解:(1)以①④为条件.
已知:如图,四边形ABCD的对角线AC与BD交于点O,OA=OC,AD∥BC.
求证:四边形ABCD为平行四边形.
证明:∵AD∥BC,
∴∠DAC=∠BCA,∠ADB=∠DBC.
又∵OA=OC,∴△AOD≌△COB,
∴AD=BC,∴四边形ABCD为平行四边形.
(2)以②④为条件,构造的命题“四边形ABCD的对角线AC与BD交于点O,AB=CD,AD∥BC,则四边形ABCD是平行四边形”为假命题.∵此时一组对边平行,另一组对边相等,可以构成等腰梯形.
16.解:作AB,DC的延长线交于点G,作DE,AF的延长线交于点H.
∵∠A=∠ABC=∠BCD=∠D=∠DEF=∠AFE,∴∠A=∠ABC=∠BCD=∠D=∠DEF=∠AFE=120°,
∴∠GBC=∠BCG=∠HFE=∠HEF=60°,∴△BCG,△HEF是等边三角形,
∴BC=BG,EF=EH,∠G=∠H=60°,
∴∠A+∠G=180°,∠D+∠G=180°,
∴AH∥GD,AG∥DH,
∴四边形AGDH是平行四边形,
∴AG=DH,
∴DE+EF=AB+BC=22.
17.解:从运动开始,要使PQ∥CD,需经过6 s.
理由如下:
设从运动开始,要使PQ∥CD,需经过t s(0≤t≤),∴AP=t cm,PD=(24-t)cm,CQ=3t cm,BQ=(26-3t)cm.
∵AD∥BC,∴PD∥QC.
又∵PQ∥CD,
∴四边形PDCQ为平行四边形,∴PD=CQ,
即24-t=3t,解得t=6.
即从运动开始,要使PQ∥CD,需经过6 s.
/
知识点 1 平行四边形判定和性质的综合应用
1.如图18-2-19,A是直线l外一点,在l上取两点B,C,分别以点A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连结AB,AD,CD.若∠ABC+∠ADC=120°,则∠A的度数是( )
A.100° B.110° C.120° D.125°
图18-2-19
图18-2-20
2.如图18-2-20,在?ABCD中,点E,F分别在BC,AD上,若要使四边形AFCE为平行四边形,需添加一个条件,则这个条件不可以是( )
A.AF=CE B.AE=CF
C.∠BAE=∠FCD D.∠BEA=∠FCE
3.如图18-2-21,在?ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,则图中平行四边形的个数是( )
A.2 B.3 C.4 D.5
图18-2-21
图18-2-22
4.如图18-2-22,在△ABC中,AB=AC=8,D是BC上一动点(点D不与点B,C重合),且DE∥AB,DF∥AC,则四边形DEAF的周长是( )
A.24 B.18 C.16 D.12
图18-2-23
5.如图18-2-23,在四边形ABCD中,已知AB=CD,AD=BC,AC,BD相交于点O,若BD=8,则DO的长为________.
6.在四边形ABCD中,对角线AC,BD相交于点O,AB∥CD,且AB=CD=16 cm,AC=18 cm,则BD长的取值范围是____________.
图18-2-24
7.如图18-2-24,已知四边形ABCD的面积为8 cm2,AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是________cm2.
8.教材例6变式如图18-2-25,在?ABCD中,点E,F分别在边AD,BC上,点M,N在对角线AC上,且AE=CF,AM=CN,求证:四边形EMFN是平行四边形.
图18-2-25
知识点 2 平行四边形判定方法的实际应用
9.小明的爸爸在钉平行四边形框架时采用了下面的方法:如图18-2-26,将两根同样长的木条AB,CD水平放置,再用木条AD,BC加固即得符合要求的框架,他的做法对吗?请说明理由.
图18-2-26
10.如图18-2-27①是某公交汽车挡风玻璃的雨刷,其工作原理如图②.雨刷EF⊥AD,垂足为A,AB=CD且AD=BC,这样能使雨刷EF在运动时,始终垂直于玻璃窗下沿BC,请证明这一结论.
图18-2-27
图18-2-16
【能力提升】
11.在?ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3 B.5
C.2或3 D.3或5
图18-2-28
12.如图18-2-28,AE∥BD,BE∥DF,AB∥CD,现给出四个结论:(1)四边形ABDC是平行四边形;(2)BE=DF;(3)S四边形ABDC=S四边形BDFE;(4)BD=CE.其中错误的有( )
A.4个 B.3个 C.2个 D.1个
13.如图18-2-29,点A,E,F,C在一条直线上,若将△DEC的EC边沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于点E,BF⊥AC于点F,且AB=CD,则当点E,F不重合时,BD与EF的关系是____________.
图18-2-29
图18-2-30
14.如图18-2-30所示,AC是?ABCD的对角线,过对角线AC上一点M任作直线EF交DC于点E,交AB于点F,要使四边形AECF是平行四边形,则点M需满足的条件是________________.
15.2018·徐州已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC;②AB=CD;③∠BAD=∠DCB;④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)构造一个真命题,画图并给出证明;
(2)构造一个假命题,举反例加以说明.
16.如图18-2-31,在六边形ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F,且AB+BC=22,试求DE+EF的值.
图18-2-31
17.如图18-2-32,在四边形ABCD中,AD∥BC,AD=24 cm,BC=26 cm.点P从点A出发,以1 cm/s的速度向点D运动;点Q从点C同时出发,以3 cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,要使PQ∥CD,需经过多少时间?为什么?
图18-2-32
答案
1.C [解析] ∵AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,AD∥BC,
∴∠A+∠ABC=180°.
∵∠ABC+∠ADC=120°,
∴∠ABC=60°,
∴∠A=120°.
故选C.
2.B [解析] A项,∵四边形ABCD是平行四边形,
∴AF∥CE.
∵AF=CE,
∴四边形AFCE是平行四边形.
∴选项A不符合题意;
B项,根据AE=CF,可知四边形AFCE可能是平行四边形,也有可能是等腰梯形,故选项B符合题意;
C项,由∠BAE=∠FCD,AB=CD,∠B=∠D可以推出△ABE≌△CDF,∴BE=DF.
∵AD=BC,∴AF=CE.
又∵AF∥CE,
∴四边形AFCE是平行四边形.
故选项C不符合题意;
D项,∵∠BEA=∠FCE,∴AE∥CF.
又∵AF∥CE,
∴四边形AFCE是平行四边形.
故选项D不符合题意.
故选B.
3.C [解析] ∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴AE=CG,
∴四边形AECG是平行四边形,
同理:四边形BFDH是平行四边形,四边形OPMN是平行四边形.
故选C.
4.C [解析] ∵AB=AC,
∴∠B=∠C.
∵DE∥AB,
∴∠B=∠CDE,
∴∠C=∠CDE,
∴CE=DE,同理可得BF=DF,
∴四边形DEAF的周长=AF+DF+DE+AE=AF+BF+CE+AE=AB+AC.
∵AB=AC=8,∴四边形DEAF的周长=8+8=16.故选C.
5.4 [解析] ∵在四边形ABCD中,AB=CD,AD=BC,∴四边形ABCD是平行四边形.∵BD=8,∴DO=4.
6.14 cm<BD<50 cm
[解析] ∵AB∥CD,AB=CD=16 cm,
∴四边形ABCD是平行四边形,
∴OC=OA,OB=OD.
∵在△OCD中,CD=16 cm,OC=9 cm,
∴CD-OC<OD<CD+OC,
即7 cm<OD<25 cm,
∴14 cm<2OD<50 cm,
即14 cm<BD<50 cm.
故答案是14 cm<BD<50 cm.
7.2 [解析] ∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴S△ADC=S△ABC=×8=4(cm2).
∵E是AB的中点,
∴S△AEC=S△ABC=×4=2(cm2).
8.证明:∵在?ABCD中,AD∥BC,
∴∠DAC=∠BCA.
又∵AE=CF,AM=CN,∴△AEM≌△CFN,
∴EM=FN,∠AME=∠CNF,
∴∠EMN=∠FNM,∴EM∥FN,
∴四边形EMFN是平行四边形.
9.解:他的做法是对的.理由:由已知得AB与CD平行且相等,根据“一组对边平行且相等的四边形是平行四边形”可知,四边形ABCD是平行四边形.
10.证明:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AD∥BC.
又∵EF⊥AD,∴EF⊥BC.
11.D
12.D [解析] 由已知可得,四边形ABDC和四边形BDFE都是平行四边形,故(1)(2)正确;又因为四边形ABDC和四边形BDFE同底等高,所以面积相等,故(3)正确;BD=AC=EF,它们与CE不一定相等,故(4)错误.故选D.
13.互相平分
14.M是AC的中点
15.解:(1)以①④为条件.
已知:如图,四边形ABCD的对角线AC与BD交于点O,OA=OC,AD∥BC.
求证:四边形ABCD为平行四边形.
证明:∵AD∥BC,
∴∠DAC=∠BCA,∠ADB=∠DBC.
又∵OA=OC,∴△AOD≌△COB,
∴AD=BC,∴四边形ABCD为平行四边形.
(2)以②④为条件,构造的命题“四边形ABCD的对角线AC与BD交于点O,AB=CD,AD∥BC,则四边形ABCD是平行四边形”为假命题.∵此时一组对边平行,另一组对边相等,可以构成等腰梯形.
16.解:作AB,DC的延长线交于点G,作DE,AF的延长线交于点H.
∵∠A=∠ABC=∠BCD=∠D=∠DEF=∠AFE,∴∠A=∠ABC=∠BCD=∠D=∠DEF=∠AFE=120°,
∴∠GBC=∠BCG=∠HFE=∠HEF=60°,∴△BCG,△HEF是等边三角形,
∴BC=BG,EF=EH,∠G=∠H=60°,
∴∠A+∠G=180°,∠D+∠G=180°,
∴AH∥GD,AG∥DH,
∴四边形AGDH是平行四边形,
∴AG=DH,
∴DE+EF=AB+BC=22.
17.解:从运动开始,要使PQ∥CD,需经过6 s.
理由如下:
设从运动开始,要使PQ∥CD,需经过t s(0≤t≤),∴AP=t cm,PD=(24-t)cm,CQ=3t cm,BQ=(26-3t)cm.
∵AD∥BC,∴PD∥QC.
又∵PQ∥CD,
∴四边形PDCQ为平行四边形,∴PD=CQ,
即24-t=3t,解得t=6.
即从运动开始,要使PQ∥CD,需经过6 s.
/
