2019-2020学年教科版(2019)必修第二册 1.2运动的合成与分解 达标作业(解析版)
文档属性
| 名称 | 2019-2020学年教科版(2019)必修第二册 1.2运动的合成与分解 达标作业(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 373.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览




文档简介
1.2运动的合成与分解
达标作业(解析版)
1.有一条两岸平直、河水均匀流动、流速恒为v的大河.小明驾着小船渡河,去程时船头指向始终与河岸垂直,回程时行驶路线与河岸垂直.去程与回程所用时间的比值为k,船在静水中的速度大小相同,则小船在静水中的速度大小为( )
A. B.
C. D.
2.如图所示,红蜡块可以在竖直玻璃管内的水中匀速上升,速度为v,若在红蜡块从A点开始匀速上升的同时,玻璃管从AB位置由静止开始水平向右做匀加速直线运动,加速度大小为a,则红蜡块的实际运动轨迹可能是图中的( )
A.直线P B.曲线Q C.曲线R D.无法确定
3.如图所示,甲、乙两船在同一条河流中同时渡河,河宽度为,河水流速为,划船速度均为,出发时两船相距,甲、乙船头均与岸边成60°角,且乙船恰好能直达正对岸A点,则下列判断正确的是
A.甲、乙两船到达对岸的时间相等
B.两船可能在未到达对岸前相遇
C.甲船一定在A点右侧靠岸
D.甲船也在A点靠岸
4.小船过河时,船头偏向上游与河岸成α角,船在静水中的速度为v,其航线恰好垂直于河岸,现水流速度稍有增大,为保持航线不变,且准时到达对岸,下列措施中可行的是
A.减小α角,增大船速v B.减小α角,保持船速v不变
C.增大α角,增大船速v D.增大α角,保持船速v不变
5.如图所示,一块橡皮用细线悬挂于O点,现用一支铅笔贴着细线的左侧水平向右以速度v匀速移动,移动过程中铅笔的高度始终不变。铅笔移动到图中虚线位置时( )
A.橡皮的速度竖直向上 B.橡皮的速度可能小于v
C.橡皮竖直方向的速度大小为 D.橡皮水平方向的速度大小为v
6.如图所示,河水由西向东流,河宽为800 m,河中各点的水流速度大小为v水,各点到较近河岸的距离为x,v水与x的关系为v水=x(m/s)(x的单位为m),让小船船头垂直河岸由南向北渡河,小船划水速度大小恒为v船=4 m/s,则下列说法中正确的是 ( )
A.小船渡河的轨迹为直线
B.小船在河水中的最大速度是5 m/s
C.小船在距南岸200 m处的速度小于在距北岸200 m处的速度
D.小船渡河的时间是160 s
7.如图所示,帆板在海面上以速度v朝正西方向运动,帆船以速度v朝正北方向航行,以帆板为参照物 ( )
A.帆船朝正东方向航行,速度大小为v
B.帆船朝正西方向航行,速度大小为v
C.帆船朝南偏东60°方向航行,速度大小为v
D.帆船朝北偏东60°方向航行,速度大小为2v
8.如图所示,物体A、B经无摩擦的定滑轮用细线连在一起,A物体受水平向右的力F的作用,此时B匀速下降,A水平向左运动,可知( )
A.物体A做匀速运动
B.物体A做加速运动
C.物体A所受摩擦力逐渐增大
D.物体A所受摩擦力不变
9.如图,图甲所示,在杂技表演中,猴子沿竖直杆向上运动,其v-t图象如图乙所示。人顶杆沿水平地面运动的s-t图象如图丙所示。若以地面为参考系,下列说法中正确的是
A.猴子的运动轨迹为直线
B.猴子在2s内做匀变速曲线运动
C.t=0时猴子的速度大小为8m/s
D.t=2s时猴子的加速度大小为4m/s2
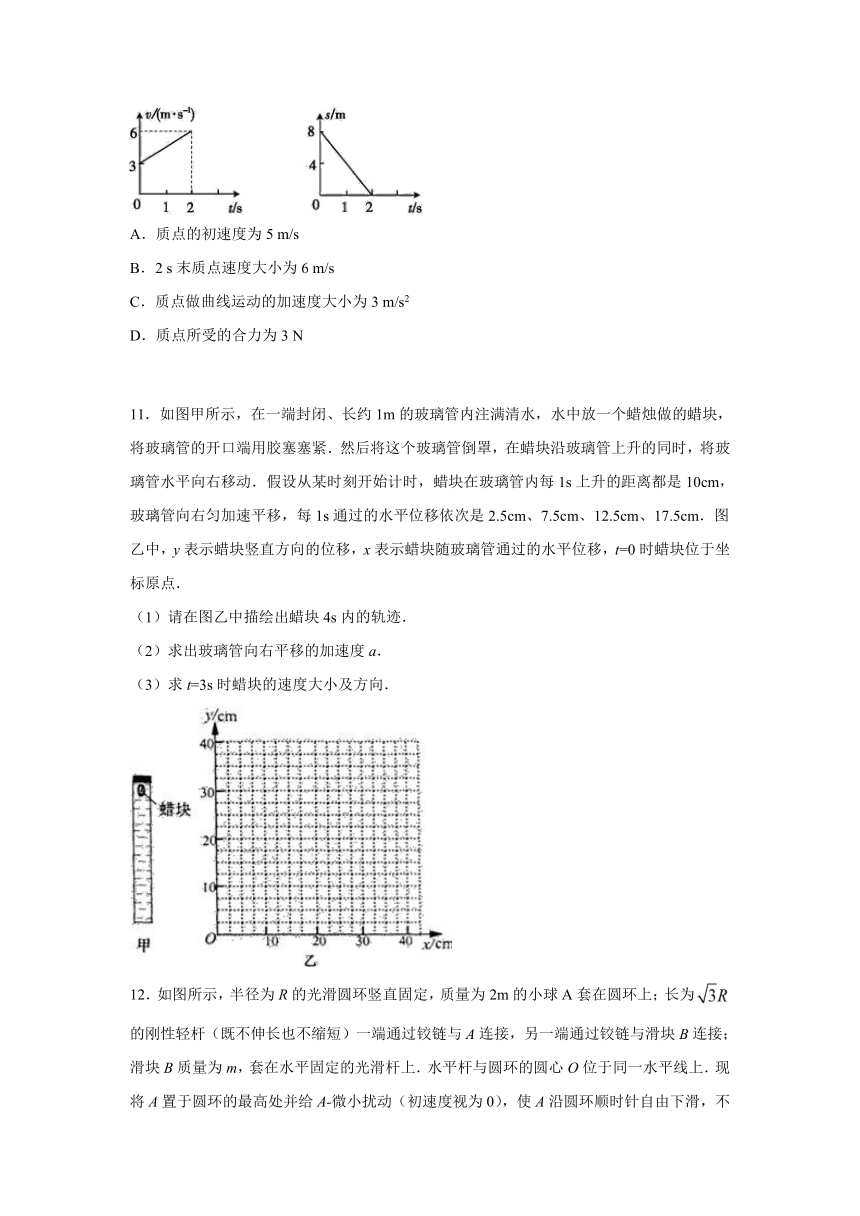
10.质量为2 kg的质点在x-y平面上做曲线运动,在x方向上的速度图象和y方向上的位移图象如图所示,下列说法正确的是 ( )
A.质点的初速度为5 m/s
B.2 s末质点速度大小为6 m/s
C.质点做曲线运动的加速度大小为3 m/s2
D.质点所受的合力为3 N
11.如图甲所示,在一端封闭、长约1m的玻璃管内注满清水,水中放一个蜡烛做的蜡块,将玻璃管的开口端用胶塞塞紧.然后将这个玻璃管倒罩,在蜡块沿玻璃管上升的同时,将玻璃管水平向右移动.假设从某时刻开始计时,蜡块在玻璃管内每1s上升的距离都是10cm,玻璃管向右匀加速平移,每1s通过的水平位移依次是2.5cm、7.5cm、12.5cm、17.5cm.图乙中,y表示蜡块竖直方向的位移,x表示蜡块随玻璃管通过的水平位移,t=0时蜡块位于坐标原点.
(1)请在图乙中描绘出蜡块4s内的轨迹.
(2)求出玻璃管向右平移的加速度a.
(3)求t=3s时蜡块的速度大小及方向.
12.如图所示,半径为R的光滑圆环竖直固定,质量为2m的小球A套在圆环上;长为的刚性轻杆(既不伸长也不缩短)一端通过铰链与A连接,另一端通过铰链与滑块B连接;滑块B质量为m,套在水平固定的光滑杆上.水平杆与圆环的圆心O位于同一水平线上.现将A置于圆环的最高处并给A-微小扰动(初速度视为0),使A沿圆环顺时针自由下滑,不计一切摩擦,A、B均视为质点,重力加速度大小为g.求:
(1)A滑到与圆心O同高度时的速度大小;
(2)A下滑至杆与圆环第一次相切的过程中,杆对B做的功.
13.如图,河宽L=60m,一只小船在河的正中央航行,经过O点时发现在距船S=40m的下游有一瀑布,为了使小船在A点安全靠岸,在O点立即调整好船头的指向,不至被冲进瀑布中.若河水的流速大小恒为5m/s,则小船的最小航行速率为__m/s.若河水的流速与到河岸的最短距离x成正比,即v水=kx(x≤,k为一常量),小船在O点调整船头垂直河岸,让小船保持航行速率不变到达A点,则小船在平行河岸方向做__运动.
14.一架飞机沿倾角方向朝斜向上方做匀速直线运动,速度是100m/s,飞机在竖直方向的分速度大小为___________m/s;经过4s,飞机在水平方向上前进了__________m.
参考答案
1.B
【解析】
【详解】
设河岸宽度为d,船的静水速度vc;去程时
t1=
回程时
t2=
又=k,得
vc=.
A. ,与结论不相符,选项A错误;
B.,与结论相符,选项B正确;
C.,与结论不相符,选项C错误;
D. ,与结论不相符,选项D错误;
故选B。
2.B
【解析】
【详解】
当合速度的方向与合力(合加速度)的方向不在同一条直线上,物体将做曲线运动,且轨迹夹在速度与合力方向之间,轨迹的凹向大致指向合力的方向;蜡块的合速度方向斜向右上方,合加速度方向水平向右,不在同一直线上,轨迹的凹向要大致指向合力的方向;
A.与分析不符,故A错误;
B.与分析相符,故B正确;
C.与分析不符,故C错误;
D.与分析不符,故D错误;
故选B。
3.A
【解析】
【详解】
A.乙船恰好能直达正对岸的A点,根据速度合成与分解,知v=2u。将小船的运动分解为平行于河岸和垂直于河岸两个方向,根据分运动和合运动具有等时性,在垂直于河岸方向上的分速度相等,知甲乙两船到达对岸的时间相等。渡河的时间,故A正确;
BCD.甲船沿河岸方向上的位移
x=(vcos60°+u)t=<2L,
知甲船在A点左侧靠岸,不可能在未到对岸前相遇。故BCD错误。
故选:A。
4.A
【解析】
【详解】
由题意可知,船在静水的速度为v,其航线恰好垂直于河岸,当水流速度稍有增大,为保持航线不变,且准时到达对岸,则合速度不变,如图所示
可知:减小a角,增大船速v; A.减小α角,增大船速v,与结论相符,选项A正确;
B.减小α角,保持船速v不变,与结论不相符,选项B错误;
C.增大α角,增大船速v,与结论不相符,选项C错误;
D.增大α角,保持船速v不变,与结论不相符,选项D错误;
故选A。
5.D
【解析】
【详解】
将铅笔与绳子接触的点的速度分解为沿绳方向和垂直于绳子方向,如图:
则沿绳子方向上的分速度为vsinθ,因为沿绳子方向上的分速度等于橡皮在竖直方向上的分速度,即为vsinθ;而橡皮在水平方向上的速度为v等于铅笔移动的速度,即为v,根据平行四边形定则,合速度为
A.橡皮水平方向和竖直方向都有速度,可知橡皮的速度不是竖直向上,选项A错误;
B.由可知,橡皮的速度大于v,选项B错误;
C.橡皮竖直方向的速度大小为,选项C错误;
D.橡皮水平方向的速度大小为v,选项D正确;
故选D。
6.B
【解析】
【详解】
A、小船的速度为沿船头指向和顺水流方向的两个分运动的分速度的矢量和,而两个分速度垂直,故当顺水流方向的分速度最大时,合速度最大,合速度的方向随顺水流方向的分速度的变化而变化,故小船到达河中心时速度最大,且运动轨迹为曲线,故A错误; B、当船到河中央时,水流速度达到最大,根据矢量的合成,船在河水中的最大速度,故B正确; C、小船距南岸200m处,则水流速度为,而小船距北岸200m处时,水流速度也为,根据速度的合成可知,它们的速度大小相等,故C错误; D、将小船的运动分解为沿船头指向和顺水流方向的两个分运动,两个分运动同时发生,互不干扰,故渡河时间与顺水流方向的分运动无关,当船头与河岸垂直时,沿船头方向的分运动的分位移最小,故渡河时间最短,最短时间为,故D错误.
【点睛】
本题关键是当船头与河岸垂直时,渡河时间最短,同时合速度与分速度遵循平行四边形定则,同时注意公式中的x的含义.
7.D
【解析】
【详解】
以帆板为参考系,即把帆板看作静止,则帆船相对于帆板有向东的速度v及向北的速度v;由矢量合成可知,二者的合速度
方向北偏东60°。 A.帆船朝正东方向航行,速度大小为v,与结论不相符,选项A错误;
B.帆船朝正西方向航行,速度大小为v,与结论不相符,选项B错误;
C.帆船朝南偏东60°方向航行,速度大小为v,与结论不相符,选项C错误;
D.帆船朝北偏东60°方向航行,速度大小为2v,与结论相符,选项D正确;
故选D。
8.B
【解析】
【详解】
B匀速下降,A沿水平面向左做运动,如图1,VB是VA在绳子方向上的分量,VB是恒定的,随着VB与水平方向的夹角增大,VA增大,所以A在水平方向上向左做加速运动.选项A错误,B正确;
因为B匀速下降,所以B受力平衡,B所受绳拉力T=GB,A受斜向上的拉力等于B的重力,在图2中把拉力分解成竖着方向的F2和水平方向的F1,在竖直方向上,有N+F2=GA.绳子与水平方向的夹角增大,所以有F2增大,支持力N减小,所以摩擦力减小,选项C错误、D正确.故选BD.
【点睛】
该题既考查了力的合成与分解,又考察了运动的合成与分解,是一道质量较高的题.该题在对A的运动的分解时,要明确谁是合速度,谁是分速度,注意物体实际运动的速度为合速度.此种情况是把合速度沿绳子收缩的方向和绳子摆动的方向进行正交分解.
9.BD
【解析】
【详解】
AB.由乙图知,猴子竖直方向上做匀减速直线运动,加速度竖直向下.由甲图知,猴子水平方向上做匀速直线运动,则猴子的加速度竖直向下,与初速度方向不在同一直线上,故猴子在2s内做匀变速曲线运动,故A错误,B正确;
C.s-t图象的斜率等于速度,则知猴子水平方向的初速度大小为,竖直方向分速度,t=0时猴子的速度大小为
,
故C错误;
D.v-t图象的斜率等于加速度,则知猴子的加速度大小为
,
故D正确。
故选BD。
10.AD
【解析】
【详解】
A.x轴方向初速度为vx=3m/s,y轴方向初速度
质点的初速度
选项A正确;
B.2 s末质点速度大小为
选项B错误;
C.质点做曲线运动的加速度大小为
选项C错误;
D.质点所受的合力为
F=ma=3 N
选项D正确;
故选AD。
11.(1)蜡块4s内的轨迹如上图所示.
(2)则玻璃管向右平移的加速度0.05m/s2.
(3)则t=3s时蜡块的速度大小m/s及方向斜向右上与水平成arctan.
【解析】
【详解】
(1)如图所示;
(2)蜡块在水平方向做匀加速运动,每相邻1秒位移差值
△x=7.5﹣2.5=12.5﹣7.5=17.5﹣12.5=5(cm)
△x=at2
解得加速度
a=0.05m/s2;
(3)vy=0.1m/s,
,
方向斜向右上与水平成arctan.
12.(1) (2)
【解析】
【详解】
(1)当A滑到与O同高度时,A的速度沿圆环切向竖直向下,B的速度为0,
由机械能守恒定律得:
解得
(2) 杆与圆环第一次相切时,A的速度沿杆方向,设为vA,此时B的速度设为vB,
根据杆不可伸长和缩短,得,其中为B的速度与水平方向的夹角
由几何关系得,则
球A下落的高度
由机械能守恒定律得
对B由动能定理得
解得
13.3 匀减速
【解析】
【详解】
[1][2].要使小船避开危险区沿直线到达对岸,则有合运动的最大位移为
OA=m=50m.
根据题目中的图,那个30m 和40m 要构成一个直角三角形的两条边,那么斜边就是50m了,那么正弦就是0.6,这是一个路程的三角形,再找一个速度的三角形,就是船速和水流速为直角边的,水流速是5m/s,而且这两个是相似三角形,所以那个正弦乘以5m/s就行了,5×0.6=3m/s
因此船的速度最小速率为3m/s;
若河水的流速与到河岸的最短距离x成正比,小船在O点调整船头垂直河岸,让小船保持航行速率不变到达A点
v水=kx=kv船t
则小船在平行河岸方向速度在均匀减小,则做匀减速直线运动;
14.50m/s 200 m
【解析】
将飞机的实际运动分解为水平方向的匀速运动和竖直方向的匀速运动,由几何关系,可得:vx=vcos60°=100×m/s=50m/s vy=vsin60°=100×=50m/s
经过4s,飞机在水平方向上前进了x=vxt=50×4m=200m.
达标作业(解析版)
1.有一条两岸平直、河水均匀流动、流速恒为v的大河.小明驾着小船渡河,去程时船头指向始终与河岸垂直,回程时行驶路线与河岸垂直.去程与回程所用时间的比值为k,船在静水中的速度大小相同,则小船在静水中的速度大小为( )
A. B.
C. D.
2.如图所示,红蜡块可以在竖直玻璃管内的水中匀速上升,速度为v,若在红蜡块从A点开始匀速上升的同时,玻璃管从AB位置由静止开始水平向右做匀加速直线运动,加速度大小为a,则红蜡块的实际运动轨迹可能是图中的( )
A.直线P B.曲线Q C.曲线R D.无法确定
3.如图所示,甲、乙两船在同一条河流中同时渡河,河宽度为,河水流速为,划船速度均为,出发时两船相距,甲、乙船头均与岸边成60°角,且乙船恰好能直达正对岸A点,则下列判断正确的是
A.甲、乙两船到达对岸的时间相等
B.两船可能在未到达对岸前相遇
C.甲船一定在A点右侧靠岸
D.甲船也在A点靠岸
4.小船过河时,船头偏向上游与河岸成α角,船在静水中的速度为v,其航线恰好垂直于河岸,现水流速度稍有增大,为保持航线不变,且准时到达对岸,下列措施中可行的是
A.减小α角,增大船速v B.减小α角,保持船速v不变
C.增大α角,增大船速v D.增大α角,保持船速v不变
5.如图所示,一块橡皮用细线悬挂于O点,现用一支铅笔贴着细线的左侧水平向右以速度v匀速移动,移动过程中铅笔的高度始终不变。铅笔移动到图中虚线位置时( )
A.橡皮的速度竖直向上 B.橡皮的速度可能小于v
C.橡皮竖直方向的速度大小为 D.橡皮水平方向的速度大小为v
6.如图所示,河水由西向东流,河宽为800 m,河中各点的水流速度大小为v水,各点到较近河岸的距离为x,v水与x的关系为v水=x(m/s)(x的单位为m),让小船船头垂直河岸由南向北渡河,小船划水速度大小恒为v船=4 m/s,则下列说法中正确的是 ( )
A.小船渡河的轨迹为直线
B.小船在河水中的最大速度是5 m/s
C.小船在距南岸200 m处的速度小于在距北岸200 m处的速度
D.小船渡河的时间是160 s
7.如图所示,帆板在海面上以速度v朝正西方向运动,帆船以速度v朝正北方向航行,以帆板为参照物 ( )
A.帆船朝正东方向航行,速度大小为v
B.帆船朝正西方向航行,速度大小为v
C.帆船朝南偏东60°方向航行,速度大小为v
D.帆船朝北偏东60°方向航行,速度大小为2v
8.如图所示,物体A、B经无摩擦的定滑轮用细线连在一起,A物体受水平向右的力F的作用,此时B匀速下降,A水平向左运动,可知( )
A.物体A做匀速运动
B.物体A做加速运动
C.物体A所受摩擦力逐渐增大
D.物体A所受摩擦力不变
9.如图,图甲所示,在杂技表演中,猴子沿竖直杆向上运动,其v-t图象如图乙所示。人顶杆沿水平地面运动的s-t图象如图丙所示。若以地面为参考系,下列说法中正确的是
A.猴子的运动轨迹为直线
B.猴子在2s内做匀变速曲线运动
C.t=0时猴子的速度大小为8m/s
D.t=2s时猴子的加速度大小为4m/s2
10.质量为2 kg的质点在x-y平面上做曲线运动,在x方向上的速度图象和y方向上的位移图象如图所示,下列说法正确的是 ( )
A.质点的初速度为5 m/s
B.2 s末质点速度大小为6 m/s
C.质点做曲线运动的加速度大小为3 m/s2
D.质点所受的合力为3 N
11.如图甲所示,在一端封闭、长约1m的玻璃管内注满清水,水中放一个蜡烛做的蜡块,将玻璃管的开口端用胶塞塞紧.然后将这个玻璃管倒罩,在蜡块沿玻璃管上升的同时,将玻璃管水平向右移动.假设从某时刻开始计时,蜡块在玻璃管内每1s上升的距离都是10cm,玻璃管向右匀加速平移,每1s通过的水平位移依次是2.5cm、7.5cm、12.5cm、17.5cm.图乙中,y表示蜡块竖直方向的位移,x表示蜡块随玻璃管通过的水平位移,t=0时蜡块位于坐标原点.
(1)请在图乙中描绘出蜡块4s内的轨迹.
(2)求出玻璃管向右平移的加速度a.
(3)求t=3s时蜡块的速度大小及方向.
12.如图所示,半径为R的光滑圆环竖直固定,质量为2m的小球A套在圆环上;长为的刚性轻杆(既不伸长也不缩短)一端通过铰链与A连接,另一端通过铰链与滑块B连接;滑块B质量为m,套在水平固定的光滑杆上.水平杆与圆环的圆心O位于同一水平线上.现将A置于圆环的最高处并给A-微小扰动(初速度视为0),使A沿圆环顺时针自由下滑,不计一切摩擦,A、B均视为质点,重力加速度大小为g.求:
(1)A滑到与圆心O同高度时的速度大小;
(2)A下滑至杆与圆环第一次相切的过程中,杆对B做的功.
13.如图,河宽L=60m,一只小船在河的正中央航行,经过O点时发现在距船S=40m的下游有一瀑布,为了使小船在A点安全靠岸,在O点立即调整好船头的指向,不至被冲进瀑布中.若河水的流速大小恒为5m/s,则小船的最小航行速率为__m/s.若河水的流速与到河岸的最短距离x成正比,即v水=kx(x≤,k为一常量),小船在O点调整船头垂直河岸,让小船保持航行速率不变到达A点,则小船在平行河岸方向做__运动.
14.一架飞机沿倾角方向朝斜向上方做匀速直线运动,速度是100m/s,飞机在竖直方向的分速度大小为___________m/s;经过4s,飞机在水平方向上前进了__________m.
参考答案
1.B
【解析】
【详解】
设河岸宽度为d,船的静水速度vc;去程时
t1=
回程时
t2=
又=k,得
vc=.
A. ,与结论不相符,选项A错误;
B.,与结论相符,选项B正确;
C.,与结论不相符,选项C错误;
D. ,与结论不相符,选项D错误;
故选B。
2.B
【解析】
【详解】
当合速度的方向与合力(合加速度)的方向不在同一条直线上,物体将做曲线运动,且轨迹夹在速度与合力方向之间,轨迹的凹向大致指向合力的方向;蜡块的合速度方向斜向右上方,合加速度方向水平向右,不在同一直线上,轨迹的凹向要大致指向合力的方向;
A.与分析不符,故A错误;
B.与分析相符,故B正确;
C.与分析不符,故C错误;
D.与分析不符,故D错误;
故选B。
3.A
【解析】
【详解】
A.乙船恰好能直达正对岸的A点,根据速度合成与分解,知v=2u。将小船的运动分解为平行于河岸和垂直于河岸两个方向,根据分运动和合运动具有等时性,在垂直于河岸方向上的分速度相等,知甲乙两船到达对岸的时间相等。渡河的时间,故A正确;
BCD.甲船沿河岸方向上的位移
x=(vcos60°+u)t=<2L,
知甲船在A点左侧靠岸,不可能在未到对岸前相遇。故BCD错误。
故选:A。
4.A
【解析】
【详解】
由题意可知,船在静水的速度为v,其航线恰好垂直于河岸,当水流速度稍有增大,为保持航线不变,且准时到达对岸,则合速度不变,如图所示
可知:减小a角,增大船速v; A.减小α角,增大船速v,与结论相符,选项A正确;
B.减小α角,保持船速v不变,与结论不相符,选项B错误;
C.增大α角,增大船速v,与结论不相符,选项C错误;
D.增大α角,保持船速v不变,与结论不相符,选项D错误;
故选A。
5.D
【解析】
【详解】
将铅笔与绳子接触的点的速度分解为沿绳方向和垂直于绳子方向,如图:
则沿绳子方向上的分速度为vsinθ,因为沿绳子方向上的分速度等于橡皮在竖直方向上的分速度,即为vsinθ;而橡皮在水平方向上的速度为v等于铅笔移动的速度,即为v,根据平行四边形定则,合速度为
A.橡皮水平方向和竖直方向都有速度,可知橡皮的速度不是竖直向上,选项A错误;
B.由可知,橡皮的速度大于v,选项B错误;
C.橡皮竖直方向的速度大小为,选项C错误;
D.橡皮水平方向的速度大小为v,选项D正确;
故选D。
6.B
【解析】
【详解】
A、小船的速度为沿船头指向和顺水流方向的两个分运动的分速度的矢量和,而两个分速度垂直,故当顺水流方向的分速度最大时,合速度最大,合速度的方向随顺水流方向的分速度的变化而变化,故小船到达河中心时速度最大,且运动轨迹为曲线,故A错误; B、当船到河中央时,水流速度达到最大,根据矢量的合成,船在河水中的最大速度,故B正确; C、小船距南岸200m处,则水流速度为,而小船距北岸200m处时,水流速度也为,根据速度的合成可知,它们的速度大小相等,故C错误; D、将小船的运动分解为沿船头指向和顺水流方向的两个分运动,两个分运动同时发生,互不干扰,故渡河时间与顺水流方向的分运动无关,当船头与河岸垂直时,沿船头方向的分运动的分位移最小,故渡河时间最短,最短时间为,故D错误.
【点睛】
本题关键是当船头与河岸垂直时,渡河时间最短,同时合速度与分速度遵循平行四边形定则,同时注意公式中的x的含义.
7.D
【解析】
【详解】
以帆板为参考系,即把帆板看作静止,则帆船相对于帆板有向东的速度v及向北的速度v;由矢量合成可知,二者的合速度
方向北偏东60°。 A.帆船朝正东方向航行,速度大小为v,与结论不相符,选项A错误;
B.帆船朝正西方向航行,速度大小为v,与结论不相符,选项B错误;
C.帆船朝南偏东60°方向航行,速度大小为v,与结论不相符,选项C错误;
D.帆船朝北偏东60°方向航行,速度大小为2v,与结论相符,选项D正确;
故选D。
8.B
【解析】
【详解】
B匀速下降,A沿水平面向左做运动,如图1,VB是VA在绳子方向上的分量,VB是恒定的,随着VB与水平方向的夹角增大,VA增大,所以A在水平方向上向左做加速运动.选项A错误,B正确;
因为B匀速下降,所以B受力平衡,B所受绳拉力T=GB,A受斜向上的拉力等于B的重力,在图2中把拉力分解成竖着方向的F2和水平方向的F1,在竖直方向上,有N+F2=GA.绳子与水平方向的夹角增大,所以有F2增大,支持力N减小,所以摩擦力减小,选项C错误、D正确.故选BD.
【点睛】
该题既考查了力的合成与分解,又考察了运动的合成与分解,是一道质量较高的题.该题在对A的运动的分解时,要明确谁是合速度,谁是分速度,注意物体实际运动的速度为合速度.此种情况是把合速度沿绳子收缩的方向和绳子摆动的方向进行正交分解.
9.BD
【解析】
【详解】
AB.由乙图知,猴子竖直方向上做匀减速直线运动,加速度竖直向下.由甲图知,猴子水平方向上做匀速直线运动,则猴子的加速度竖直向下,与初速度方向不在同一直线上,故猴子在2s内做匀变速曲线运动,故A错误,B正确;
C.s-t图象的斜率等于速度,则知猴子水平方向的初速度大小为,竖直方向分速度,t=0时猴子的速度大小为
,
故C错误;
D.v-t图象的斜率等于加速度,则知猴子的加速度大小为
,
故D正确。
故选BD。
10.AD
【解析】
【详解】
A.x轴方向初速度为vx=3m/s,y轴方向初速度
质点的初速度
选项A正确;
B.2 s末质点速度大小为
选项B错误;
C.质点做曲线运动的加速度大小为
选项C错误;
D.质点所受的合力为
F=ma=3 N
选项D正确;
故选AD。
11.(1)蜡块4s内的轨迹如上图所示.
(2)则玻璃管向右平移的加速度0.05m/s2.
(3)则t=3s时蜡块的速度大小m/s及方向斜向右上与水平成arctan.
【解析】
【详解】
(1)如图所示;
(2)蜡块在水平方向做匀加速运动,每相邻1秒位移差值
△x=7.5﹣2.5=12.5﹣7.5=17.5﹣12.5=5(cm)
△x=at2
解得加速度
a=0.05m/s2;
(3)vy=0.1m/s,
,
方向斜向右上与水平成arctan.
12.(1) (2)
【解析】
【详解】
(1)当A滑到与O同高度时,A的速度沿圆环切向竖直向下,B的速度为0,
由机械能守恒定律得:
解得
(2) 杆与圆环第一次相切时,A的速度沿杆方向,设为vA,此时B的速度设为vB,
根据杆不可伸长和缩短,得,其中为B的速度与水平方向的夹角
由几何关系得,则
球A下落的高度
由机械能守恒定律得
对B由动能定理得
解得
13.3 匀减速
【解析】
【详解】
[1][2].要使小船避开危险区沿直线到达对岸,则有合运动的最大位移为
OA=m=50m.
根据题目中的图,那个30m 和40m 要构成一个直角三角形的两条边,那么斜边就是50m了,那么正弦就是0.6,这是一个路程的三角形,再找一个速度的三角形,就是船速和水流速为直角边的,水流速是5m/s,而且这两个是相似三角形,所以那个正弦乘以5m/s就行了,5×0.6=3m/s
因此船的速度最小速率为3m/s;
若河水的流速与到河岸的最短距离x成正比,小船在O点调整船头垂直河岸,让小船保持航行速率不变到达A点
v水=kx=kv船t
则小船在平行河岸方向速度在均匀减小,则做匀减速直线运动;
14.50m/s 200 m
【解析】
将飞机的实际运动分解为水平方向的匀速运动和竖直方向的匀速运动,由几何关系,可得:vx=vcos60°=100×m/s=50m/s vy=vsin60°=100×=50m/s
经过4s,飞机在水平方向上前进了x=vxt=50×4m=200m.
同课章节目录
- 第一章 抛体运动
- 1 认识曲线运动
- 2 运动的合成与分解
- 3 探究平抛运动的特点
- 4 研究平抛运动的规律
- 5 斜抛运动(选学)
- 第二章 匀速圆周运动
- 1 圆周运动
- 2 匀速圆周运动的向心力和向心加速度
- 3 圆周运动的实例分析
- 4 圆周运动与人类文明(选学)
- 第三章 万有引力定律
- 1 天体运动
- 2 万有引力定律
- 3 预言未知星体 计算天体质量
- 4 人造卫星宇宙
- 5 太空探索(选学)
- 第四章 机械能及其守恒定律
- 1 功
- 2 功率
- 3 动能 动能定理
- 4 势能
- 5 机械能守恒定律
- 6 实验:验证机械能守恒定律
- 第五章 经典力学的局限性与相对论初步
- 1 经典力学的成就与局限性
- 2 相对论时空观简介
- 3 宇宙的起源和演化
