2020年人教版七年级数学下册同步练习附答案5.1.1相交线
文档属性
| 名称 | 2020年人教版七年级数学下册同步练习附答案5.1.1相交线 |

|
|
| 格式 | zip | ||
| 文件大小 | 106.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览



文档简介
5.1.1相交线
知识要点:
1.定义:两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,互为邻补角.
2.邻补角是成对出现的,单独的一个角不能称为邻补角,两条直线相交形成四对邻补角.
3.性质:邻补角互补
4.定义:两个角有一个公共的顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种关系的两个角,互为对顶角.
5.性质:对顶角相等.但相等的角不一定是对顶角.
注意:
识别对顶角时,要抓住两个关键要素:一是顶点,二是边.先看两个角是否有公共顶点,再看两个角的两边是否分别互为反向延长线.两条直线相交形成两对对顶角.
一、单选题
1.如图,对于直线AB,线段CD,射线EF,其中能相交的图是( )
A. B.
C. D.
2.如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )
A.25° B.35° C.45° D.55°
3.如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于( ).
A.35° B.70°
C.110° D.145°
4.如图,∠1=100°,∠2=145°,那么∠3=( ).
A.55° B.65° C.75° D.85°
5.如图,直线AB、CD相交于点O,且∠AOD+∠BOC=100°,则∠AOC是( )
A.150° B.130° C.100° D.90°
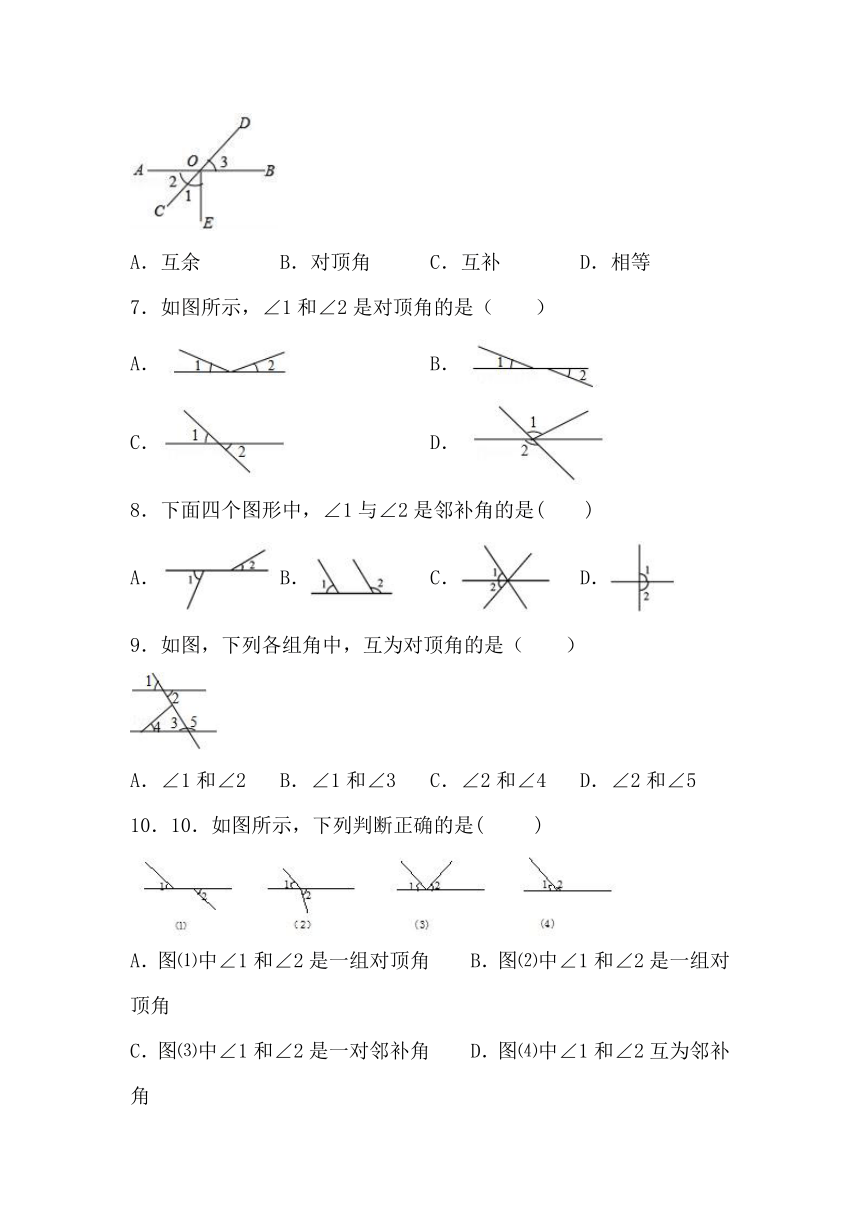
6.如图,直线AB,CD交于O,EO⊥AB于O,∠1与∠3的关系是( )
A.互余 B.对顶角 C.互补 D.相等
7.如图所示,∠1和∠2是对顶角的是( )
A. B.
C. D.
8.下面四个图形中,∠1与∠2是邻补角的是( )
A. B. C. D.
9.如图,下列各组角中,互为对顶角的是( )
A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5
10.10.如图所示,下列判断正确的是( )
A.图⑴中∠1和∠2是一组对顶角 B.图⑵中∠1和∠2是一组对顶角
C.图⑶中∠1和∠2是一对邻补角 D.图⑷中∠1和∠2互为邻补角
二、填空题
11.如图所示,AB∥CD,EF与AB,CD相交,EF与AB交于点_____,EF与CD交于______.
12.两条直线相交,只有_____个交点.
13.平面内四条直线共有三个交点,则这四条直线中最多有________ 条平行线.
14.探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有_________对,邻补角有__________对.
三、解答题
15.平面上两条直线相交于一点,三条直线俩两相交,每个交点都不经过第三条直线.
(1)5条直线的交点为_____个.
(2)请探索n条直线的交点个数.
16.如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
(1)求∠AON的度数.
(2)写出∠DON的余角.
17.如图,直线AB与CD相交于点O,∠AOC∶∠AOD=1∶2.求∠BOD的度数.
18.如图,三条直线AB,CD,EF交于一点,若∠1=30°,∠2=70°,求∠3的度数.
答案
1.B
2.D
3.C
4.B
5.B
6.A
7.C
8.D
9.A
10.D
11.M N
12. 1.
13.三
14.(1)1,3;(2)1,6;(3)1,,n(n-1),2n(n-1)
15.(1)
如图所示: 我们发现:2条直线相交有1个交点; 3条直线相交有1+2=3个交点; 4条直线相交有1+2+3=6个交点, 则5条直线的交点为1+2+3+4=10; (2)图(n):1+2+3+…+n-1=.
16.(1)∵∠AOC+∠AOD=∠AOD+∠BOD=180°,
∴∠BOD=∠AOC=50°,
∵OM平分∠BOD,
∴∠BOM=∠DOM=25°,
又由∠MON=90°,
∴∠AON=180°﹣(∠MON+∠BOM)=180°﹣(90°+25°)=65°;
(2)由∠DON+∠DOM=∠MON=90°知∠DOM为∠DON的余角,
∵∠AON+∠BOM=90°,∠DOM=∠MOB,
∴∠AON+∠DOM=90°,
∴∠NOD+∠BOM=90°,
故∠DON的余角为:∠DOM,∠BOM.
17.由邻补角的性质,得∠AOC+∠AOD=180°.
由∠AOC∶∠AOD=1∶2,
得∠AOD=2∠AOC,
∠AOC+2∠AOC=180°,
解得∠AOC=60°.
由对顶角相等,得∠BOD=∠AOC=60°.
故答案为:60°.
18.解:如图,∵∠4=∠2=70°(对顶角相等),
∴∠3=180°-∠1-∠4=180°-30°-70°=80°.
知识要点:
1.定义:两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,互为邻补角.
2.邻补角是成对出现的,单独的一个角不能称为邻补角,两条直线相交形成四对邻补角.
3.性质:邻补角互补
4.定义:两个角有一个公共的顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种关系的两个角,互为对顶角.
5.性质:对顶角相等.但相等的角不一定是对顶角.
注意:
识别对顶角时,要抓住两个关键要素:一是顶点,二是边.先看两个角是否有公共顶点,再看两个角的两边是否分别互为反向延长线.两条直线相交形成两对对顶角.
一、单选题
1.如图,对于直线AB,线段CD,射线EF,其中能相交的图是( )
A. B.
C. D.
2.如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )
A.25° B.35° C.45° D.55°
3.如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于( ).
A.35° B.70°
C.110° D.145°
4.如图,∠1=100°,∠2=145°,那么∠3=( ).
A.55° B.65° C.75° D.85°
5.如图,直线AB、CD相交于点O,且∠AOD+∠BOC=100°,则∠AOC是( )
A.150° B.130° C.100° D.90°
6.如图,直线AB,CD交于O,EO⊥AB于O,∠1与∠3的关系是( )
A.互余 B.对顶角 C.互补 D.相等
7.如图所示,∠1和∠2是对顶角的是( )
A. B.
C. D.
8.下面四个图形中,∠1与∠2是邻补角的是( )
A. B. C. D.
9.如图,下列各组角中,互为对顶角的是( )
A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5
10.10.如图所示,下列判断正确的是( )
A.图⑴中∠1和∠2是一组对顶角 B.图⑵中∠1和∠2是一组对顶角
C.图⑶中∠1和∠2是一对邻补角 D.图⑷中∠1和∠2互为邻补角
二、填空题
11.如图所示,AB∥CD,EF与AB,CD相交,EF与AB交于点_____,EF与CD交于______.
12.两条直线相交,只有_____个交点.
13.平面内四条直线共有三个交点,则这四条直线中最多有________ 条平行线.
14.探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有_________对,邻补角有__________对.
三、解答题
15.平面上两条直线相交于一点,三条直线俩两相交,每个交点都不经过第三条直线.
(1)5条直线的交点为_____个.
(2)请探索n条直线的交点个数.
16.如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
(1)求∠AON的度数.
(2)写出∠DON的余角.
17.如图,直线AB与CD相交于点O,∠AOC∶∠AOD=1∶2.求∠BOD的度数.
18.如图,三条直线AB,CD,EF交于一点,若∠1=30°,∠2=70°,求∠3的度数.
答案
1.B
2.D
3.C
4.B
5.B
6.A
7.C
8.D
9.A
10.D
11.M N
12. 1.
13.三
14.(1)1,3;(2)1,6;(3)1,,n(n-1),2n(n-1)
15.(1)
如图所示: 我们发现:2条直线相交有1个交点; 3条直线相交有1+2=3个交点; 4条直线相交有1+2+3=6个交点, 则5条直线的交点为1+2+3+4=10; (2)图(n):1+2+3+…+n-1=.
16.(1)∵∠AOC+∠AOD=∠AOD+∠BOD=180°,
∴∠BOD=∠AOC=50°,
∵OM平分∠BOD,
∴∠BOM=∠DOM=25°,
又由∠MON=90°,
∴∠AON=180°﹣(∠MON+∠BOM)=180°﹣(90°+25°)=65°;
(2)由∠DON+∠DOM=∠MON=90°知∠DOM为∠DON的余角,
∵∠AON+∠BOM=90°,∠DOM=∠MOB,
∴∠AON+∠DOM=90°,
∴∠NOD+∠BOM=90°,
故∠DON的余角为:∠DOM,∠BOM.
17.由邻补角的性质,得∠AOC+∠AOD=180°.
由∠AOC∶∠AOD=1∶2,
得∠AOD=2∠AOC,
∠AOC+2∠AOC=180°,
解得∠AOC=60°.
由对顶角相等,得∠BOD=∠AOC=60°.
故答案为:60°.
18.解:如图,∵∠4=∠2=70°(对顶角相等),
∴∠3=180°-∠1-∠4=180°-30°-70°=80°.
