2020春北师大版八年级数学下册1.2直角三角形(第2课时)教学课件(17张)
文档属性
| 名称 | 2020春北师大版八年级数学下册1.2直角三角形(第2课时)教学课件(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 219.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 12:07:17 | ||
图片预览


文档简介
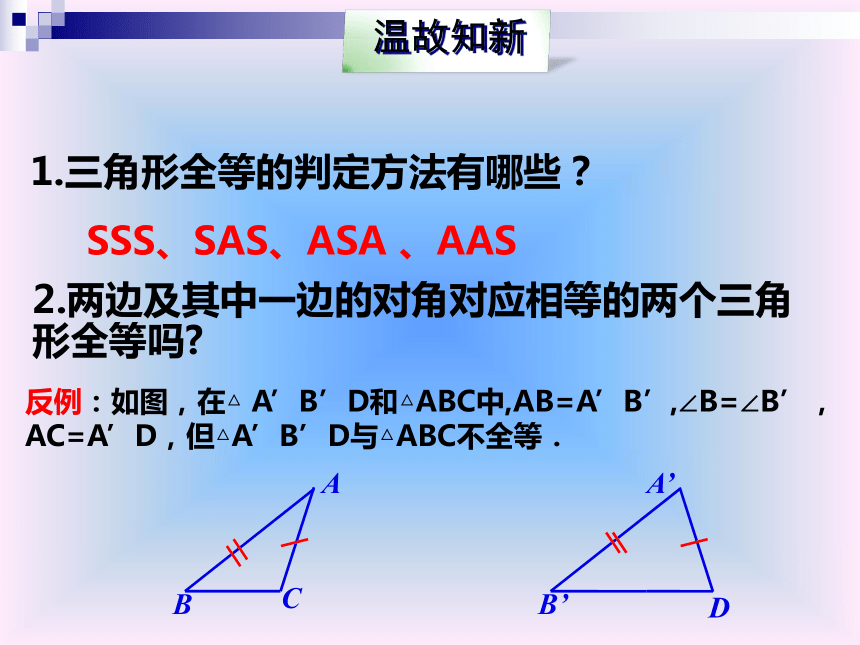
课件17张PPT。第二节 直角三角形(2)北师大版 八年级下册第一章 三角形的证明1.三角形全等的判定方法有哪些?SSS、SAS、ASA 、AAS2.两边及其中一边的对角对应相等的两个三角形全等吗?反例:如图,在△ A’B’D和△ABC中,AB=A’B’,∠B=∠B’,AC=A’D,但△A’B’D与△ABC不全等.思考:如果其中一边的所对的角是直角呢?操作:
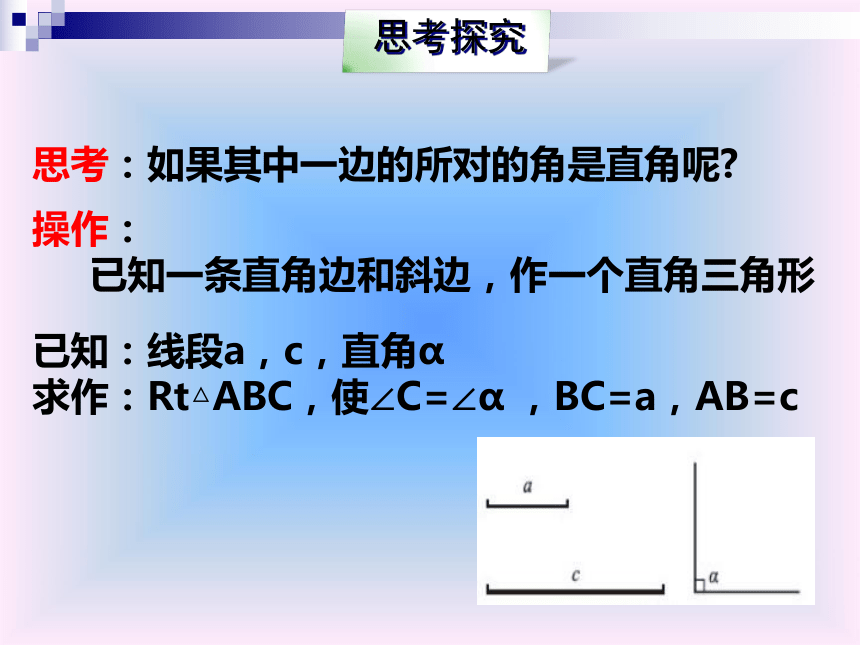
已知一条直角边和斜边,作一个直角三角形已知:线段a,c,直角α
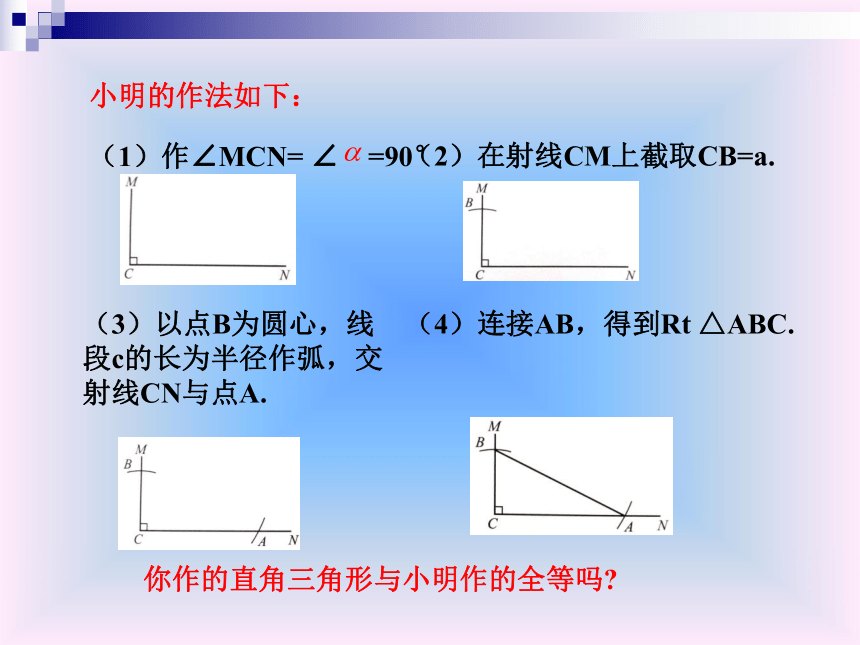
求作:Rt△ABC,使∠C=∠α ,BC=a,AB=c你作的直角三角形与小明作的全等吗?小明的作法如下:(1)作∠MCN= ∠ =90°(2)在射线CM上截取CB=a.(3)以点B为圆心,线段c的长为半径作弧,交射线CN与点A.(4)连接AB,得到Rt △ABC.观察:你和同学作出的三角形是否全等?如果把你们所作的三角形都剪下来重叠,它们是否完全重合?猜想:斜边和一条直角边对应相等的两个直角三角形全等;证明:∵△ABC中,∠C=90°
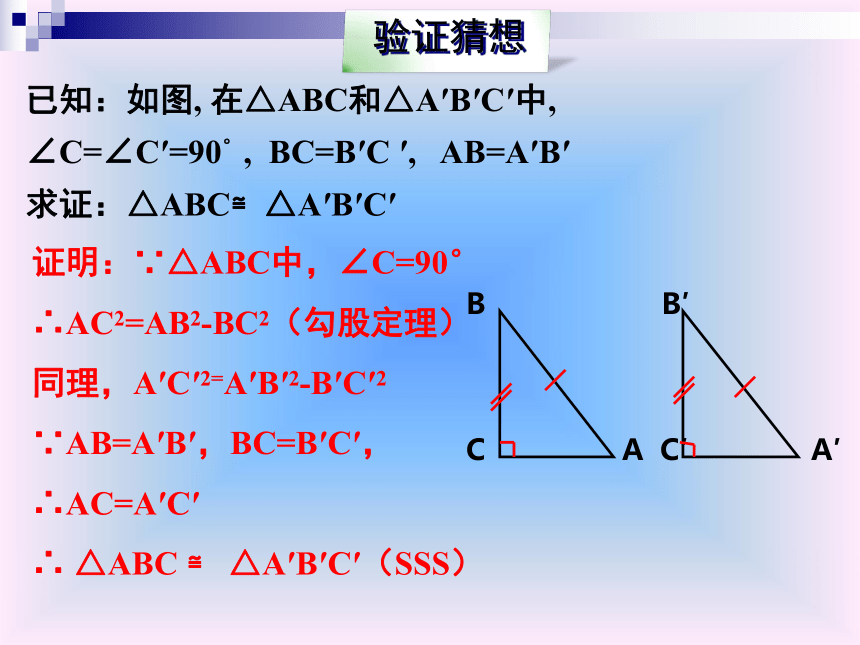
∴AC2=AB2-BC2(勾股定理)
同理,A′C′2=A′B′2-B′C′2
∵AB=A′B′,BC=B′C′,
∴AC=A′C′
∴ △ABC ≌ △A′B′C′(SSS) 已知:如图, 在△ABC和△A′B′C′中,
∠C=∠C′=90°, BC=B′C ′, AB=A′B′
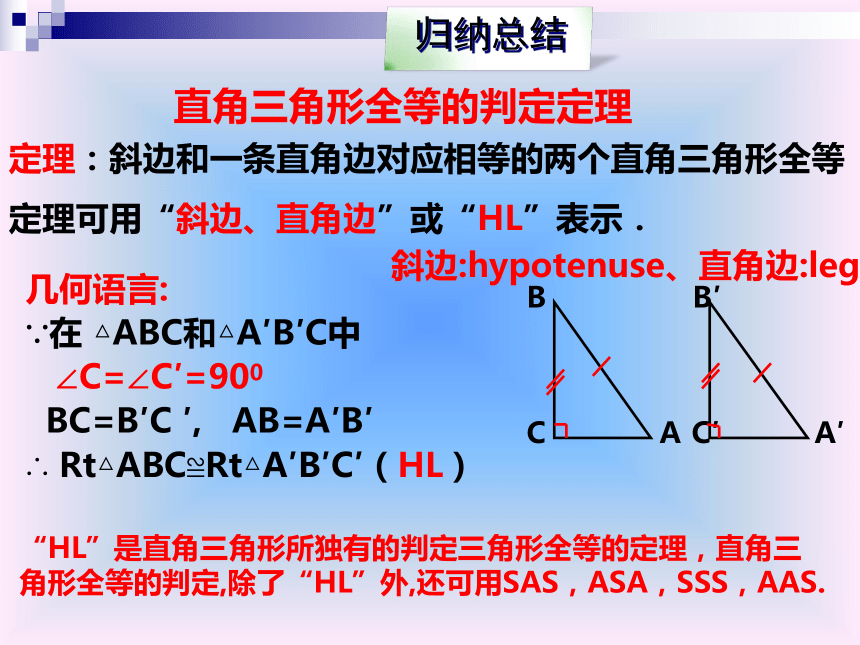
求证:△ABC≌△A′B′C′ 定理:斜边和一条直角边对应相等的两个直角三角形全等
定理可用“斜边、直角边”或“HL”表示.直角三角形全等的判定定理几何语言:
∵在 △ABC和△A′B′C中
∠C=∠C′=900
BC=B′C ′, AB=A′B′
∴ Rt△ABC≌Rt△A′B′C′(HL)“HL”是直角三角形所独有的判定三角形全等的定理,直角三角形全等的判定,除了“HL”外,还可用SAS,ASA,SSS,AAS.斜边:hypotenuse、直角边:leg例:有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小关系?解:由题意,得,∠BAC=∠EDF=90°
BC=EF,AC=DF
∴Rt△BAC≌Rt△EDF (HL)
∴∠B=∠DEF (全等三角形对应角相等)
∵∠DEF+∠F=90°(直角三角形两锐角互余)
∴∠B+∠F=90°1.判断下列命题的真假,并说明理由:
(1)两个锐角对应相等的两个直角三角形全等;
(2)斜边及一锐角对应相等的两个直角三角形全等;
(3)两条直角边对应相等的两个直角三角形全等;
(4)一条直角边及另一条直角边上的中线相等的两个直角三角形假真真真2.如图,已知∠ACB=∠BDA=90°,要使△ACB≌ △ BDA,还需要什么条件?添加条件:
添加角:∠CBA=∠DAB或∠CAB=∠DBA(AAS)
添加边:AC=BD或BC=AD.(HL) 题目隐含条件:AB=BA3.如图,两根长度为12m的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗?说明理由。解:相等;根据题意,可知∠AOC=∠AOB=90°,
AB=AC,AO=AO
∴Rt△AOB≌Rt△AOC (HL)
∴ OB=OC (全等三角形对应边相等)4.如图,在△ABC中,AB=CB,∠ABC=90°,点F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF的度数.(1)证明:∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∵AE=CF,AB=BC,
∴Rt△ABE≌Rt△CBF(HL).
(2)解:∵AB=BC,∠ABC=90°,
∴∠CAB=∠ACB=45°.
∵∠BAE=∠CAB-∠CAE=45°-30°=15°.
由(1)知Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°.
∴∠ACF=∠BCF+∠ACB=45°+15°=60°.1.“HL”定理
2.总结:直角三角形全等的判定方法.四、课堂小结五、布置作业1.从教材习题1.6中的第1、2、3、4、5题1.已知:如图,D是△ABC的BC边的中点,DE⊥AC,DF⊥AB,垂足分别是E.F,且DE=DF,
求证:△ABC是等腰三角形证明:∵ D是△ABC的BC边的中点
∴BD=CD
∵ DE⊥AC,DF⊥AB
∴∠1=∠2=90°
∵BD=CD,DE=DF
∴Rt△BDF≌Rt△CDE (HL)
∴∠B=∠C
∴△ABC是等腰三角形
2.已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为EF,且DE=BF,求证:(1)AE=CF(2)AB∥CD证明:(1)∵ DE⊥AC,BF⊥AC
∴∠1=∠2=90°
∵AB=CD,DE=BF
∴Rt△ABF≌Rt△CDE (HL)
∴AF=CE
∴AF-EF=CE-EF
即AE=CF
(2) ∵Rt△ABF≌Rt△CDE (HL)
∴∠A=∠C ∴AB∥CD(内错角相等,两直线平行)
已知一条直角边和斜边,作一个直角三角形已知:线段a,c,直角α
求作:Rt△ABC,使∠C=∠α ,BC=a,AB=c你作的直角三角形与小明作的全等吗?小明的作法如下:(1)作∠MCN= ∠ =90°(2)在射线CM上截取CB=a.(3)以点B为圆心,线段c的长为半径作弧,交射线CN与点A.(4)连接AB,得到Rt △ABC.观察:你和同学作出的三角形是否全等?如果把你们所作的三角形都剪下来重叠,它们是否完全重合?猜想:斜边和一条直角边对应相等的两个直角三角形全等;证明:∵△ABC中,∠C=90°
∴AC2=AB2-BC2(勾股定理)
同理,A′C′2=A′B′2-B′C′2
∵AB=A′B′,BC=B′C′,
∴AC=A′C′
∴ △ABC ≌ △A′B′C′(SSS) 已知:如图, 在△ABC和△A′B′C′中,
∠C=∠C′=90°, BC=B′C ′, AB=A′B′
求证:△ABC≌△A′B′C′ 定理:斜边和一条直角边对应相等的两个直角三角形全等
定理可用“斜边、直角边”或“HL”表示.直角三角形全等的判定定理几何语言:
∵在 △ABC和△A′B′C中
∠C=∠C′=900
BC=B′C ′, AB=A′B′
∴ Rt△ABC≌Rt△A′B′C′(HL)“HL”是直角三角形所独有的判定三角形全等的定理,直角三角形全等的判定,除了“HL”外,还可用SAS,ASA,SSS,AAS.斜边:hypotenuse、直角边:leg例:有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小关系?解:由题意,得,∠BAC=∠EDF=90°
BC=EF,AC=DF
∴Rt△BAC≌Rt△EDF (HL)
∴∠B=∠DEF (全等三角形对应角相等)
∵∠DEF+∠F=90°(直角三角形两锐角互余)
∴∠B+∠F=90°1.判断下列命题的真假,并说明理由:
(1)两个锐角对应相等的两个直角三角形全等;
(2)斜边及一锐角对应相等的两个直角三角形全等;
(3)两条直角边对应相等的两个直角三角形全等;
(4)一条直角边及另一条直角边上的中线相等的两个直角三角形假真真真2.如图,已知∠ACB=∠BDA=90°,要使△ACB≌ △ BDA,还需要什么条件?添加条件:
添加角:∠CBA=∠DAB或∠CAB=∠DBA(AAS)
添加边:AC=BD或BC=AD.(HL) 题目隐含条件:AB=BA3.如图,两根长度为12m的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗?说明理由。解:相等;根据题意,可知∠AOC=∠AOB=90°,
AB=AC,AO=AO
∴Rt△AOB≌Rt△AOC (HL)
∴ OB=OC (全等三角形对应边相等)4.如图,在△ABC中,AB=CB,∠ABC=90°,点F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF的度数.(1)证明:∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∵AE=CF,AB=BC,
∴Rt△ABE≌Rt△CBF(HL).
(2)解:∵AB=BC,∠ABC=90°,
∴∠CAB=∠ACB=45°.
∵∠BAE=∠CAB-∠CAE=45°-30°=15°.
由(1)知Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°.
∴∠ACF=∠BCF+∠ACB=45°+15°=60°.1.“HL”定理
2.总结:直角三角形全等的判定方法.四、课堂小结五、布置作业1.从教材习题1.6中的第1、2、3、4、5题1.已知:如图,D是△ABC的BC边的中点,DE⊥AC,DF⊥AB,垂足分别是E.F,且DE=DF,
求证:△ABC是等腰三角形证明:∵ D是△ABC的BC边的中点
∴BD=CD
∵ DE⊥AC,DF⊥AB
∴∠1=∠2=90°
∵BD=CD,DE=DF
∴Rt△BDF≌Rt△CDE (HL)
∴∠B=∠C
∴△ABC是等腰三角形
2.已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为EF,且DE=BF,求证:(1)AE=CF(2)AB∥CD证明:(1)∵ DE⊥AC,BF⊥AC
∴∠1=∠2=90°
∵AB=CD,DE=BF
∴Rt△ABF≌Rt△CDE (HL)
∴AF=CE
∴AF-EF=CE-EF
即AE=CF
(2) ∵Rt△ABF≌Rt△CDE (HL)
∴∠A=∠C ∴AB∥CD(内错角相等,两直线平行)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
