人教A版高中数学必修4课件:2.2.2向量减法运算及其几何意义 (共14张PPT)
文档属性
| 名称 | 人教A版高中数学必修4课件:2.2.2向量减法运算及其几何意义 (共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 386.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
2.2.2向量减法运算及其几何意义
人教版高中数学必修四
(1)你还能回想起实数的相反数是怎样定义的吗?
(2)两个实数的减法运算可以看成加法运算吗?
思考:
如设
实数 的相反数记作 。
如何定义向量的减法运算呢?
回顾:
一、相反向量:
规定:
设向量 ,我们把与 长度相同,方向相反
的向量叫做 的相反向量。
(1)
(3)设 互为相反向量,那么
记作:
的相反向量仍是 。
二、向量的减法:
(2)
B
A
C
设
D
E
又
所以
你能利用我们学过的向量的加法法则作出 吗?
不借助向量的加法法则你能直接作出 吗?
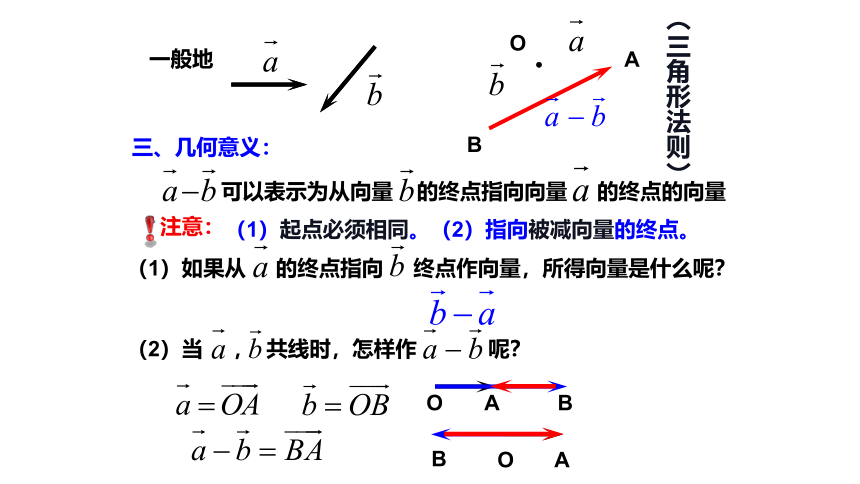
三、几何意义:
可以表示为从向量 的终点指向向量 的终点的向量
(1)如果从 的终点指向 终点作向量,所得向量是什么呢?
(2)当 , 共线时,怎样作 呢?
A
B
O
A
B
O
注意:
(1)起点必须相同。(2)指向被减向量的终点。
一般地
B
A
O
(三角形法则)
三、几何意义
注意:
(1)起点必须相同。(2)指向被减向量的终点。
一般地
B
A
O
可以表示为从向量 的终点指向向量 的终点的向量
练习:
已知向量 ,求作向量 , 。
例3
O
B
A
C
D
作法:
在平面内任取一点O,
则
作
记忆口诀:
起点相同,连接终点,指向被减向量的终点。
练习1:
已知向量 ,求作向量 。
(1)
(2)
(3)
(4)
例4
在 ABCD 中,
你能用 表示 吗?
D
B
A
C
变式一 本例中,当 满足什么条件时,
与 互相垂直?
变式二 本例中,当 满足什么条件时,
向量的减法
一、定义(利用向量的加法定义)。
二、向量减法三角形法则
(口诀:起点相同,连终点,指向被减向量)。
作业:
习题2.2 P91页 第4题
2.2.2向量减法运算及其几何意义
人教版高中数学必修四
(1)你还能回想起实数的相反数是怎样定义的吗?
(2)两个实数的减法运算可以看成加法运算吗?
思考:
如设
实数 的相反数记作 。
如何定义向量的减法运算呢?
回顾:
一、相反向量:
规定:
设向量 ,我们把与 长度相同,方向相反
的向量叫做 的相反向量。
(1)
(3)设 互为相反向量,那么
记作:
的相反向量仍是 。
二、向量的减法:
(2)
B
A
C
设
D
E
又
所以
你能利用我们学过的向量的加法法则作出 吗?
不借助向量的加法法则你能直接作出 吗?
三、几何意义:
可以表示为从向量 的终点指向向量 的终点的向量
(1)如果从 的终点指向 终点作向量,所得向量是什么呢?
(2)当 , 共线时,怎样作 呢?
A
B
O
A
B
O
注意:
(1)起点必须相同。(2)指向被减向量的终点。
一般地
B
A
O
(三角形法则)
三、几何意义
注意:
(1)起点必须相同。(2)指向被减向量的终点。
一般地
B
A
O
可以表示为从向量 的终点指向向量 的终点的向量
练习:
已知向量 ,求作向量 , 。
例3
O
B
A
C
D
作法:
在平面内任取一点O,
则
作
记忆口诀:
起点相同,连接终点,指向被减向量的终点。
练习1:
已知向量 ,求作向量 。
(1)
(2)
(3)
(4)
例4
在 ABCD 中,
你能用 表示 吗?
D
B
A
C
变式一 本例中,当 满足什么条件时,
与 互相垂直?
变式二 本例中,当 满足什么条件时,
向量的减法
一、定义(利用向量的加法定义)。
二、向量减法三角形法则
(口诀:起点相同,连终点,指向被减向量)。
作业:
习题2.2 P91页 第4题
