北师大版七年级数学下册第二章相交线与平行线章末复习课件(共42张PPT)
文档属性
| 名称 | 北师大版七年级数学下册第二章相交线与平行线章末复习课件(共42张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览





文档简介
(共42张PPT)
章末复习
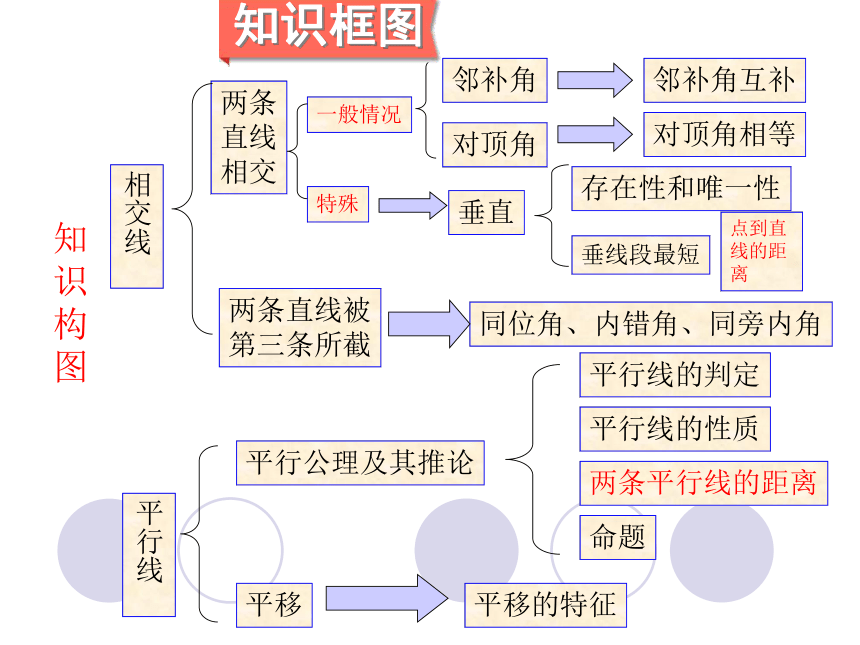
相交线
两条
直线
相交
两条直线被
第三条所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
平行线的判定
平行线的性质
两条平行线的距离
平移
平移的特征
命题
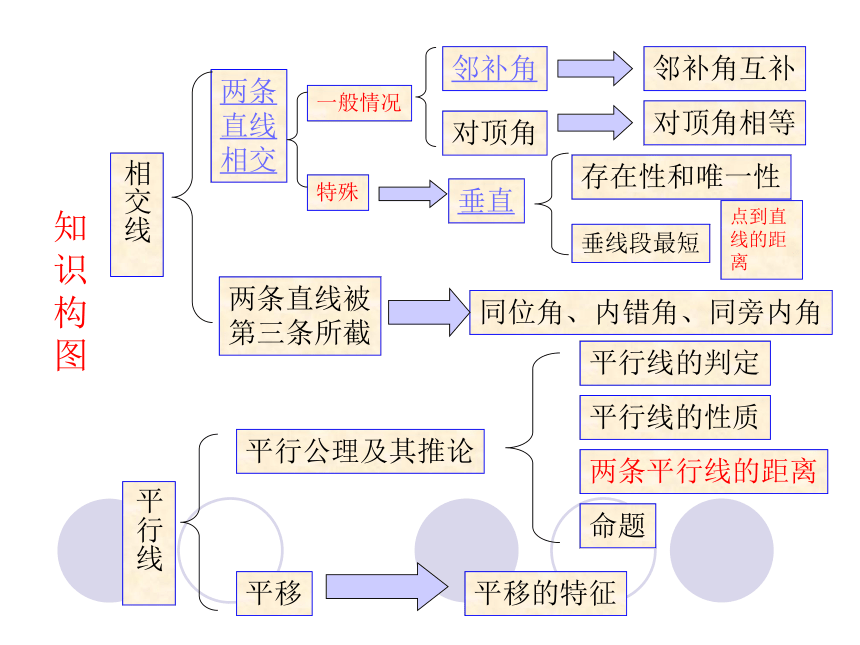
知识构图
知识框图
相交线
两条
直线
相交
两条直线被
第三条所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
平行线的判定
平行线的性质
两条平行线的距离
平移
平移的特征
命题
知识构图
(1)两条直线相交所构成的四个角中,
有公共顶点但没有公共边的两个角是对顶角。
如图(2).
(2)一个角的两边分别是另一个角的两边的反向延长线,这两个角是对顶角。
同角的补角相等。
对顶角相等。
两个特征:(1) 具有公共顶点;
(2) 角的两边互为反向延长线。
n条直线相交于一点,
就有n(n-1)对对顶角。
1
2
(1)
(2)
1
2
3
4
两条直线相交所构成的四了角中,有公共顶点且有一条公共边的两个角是邻补角.如图(1)
1.互为邻补角:
2. 对顶角:
3. 邻补角的性质:
4. 对顶角性质:
巩固旧识
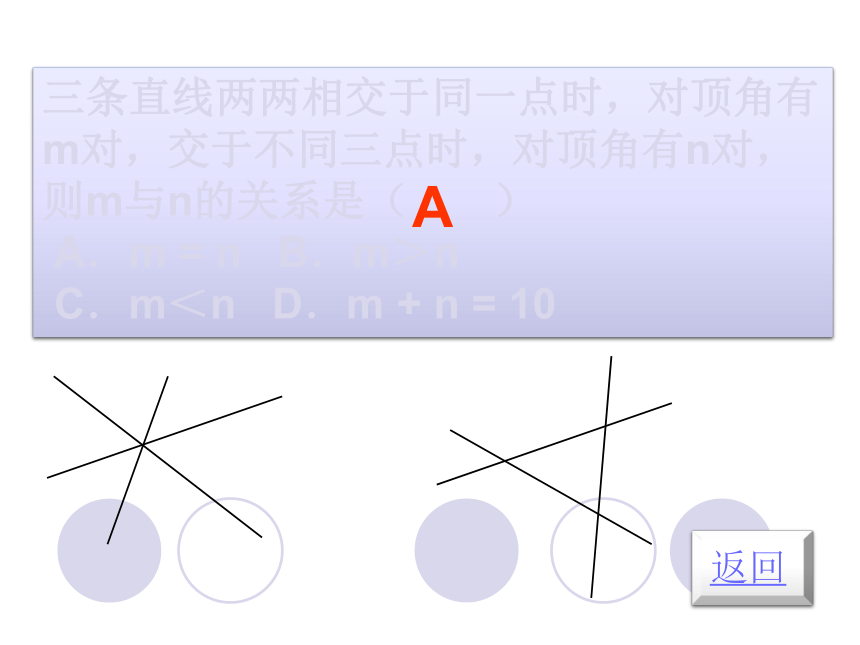
三条直线两两相交于同一点时,对顶角有m对,交于不同三点时,对顶角有n对,则m与n的关系是( )
A.m = n B.m>n
C.m<n D.m + n = 10
A
返回
A
B
C
D
O
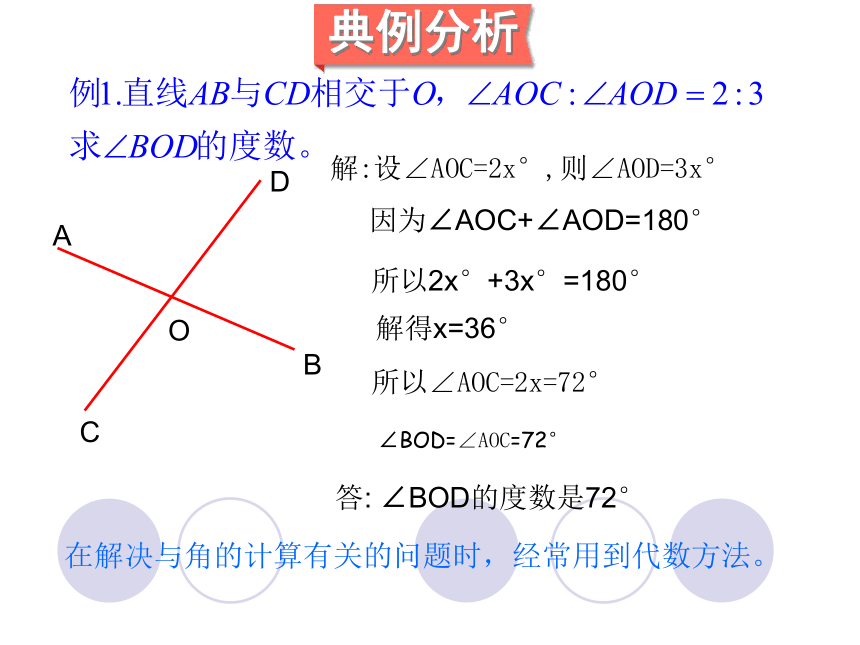
在解决与角的计算有关的问题时,经常用到代数方法。
解:设∠AOC=2x°,则∠AOD=3x°
所以2x°+3x°=180°
因为∠AOC+∠AOD=180°
解得x=36°
所以∠AOC=2x=72°
∠BOD=∠AOC=72°
答: ∠BOD的度数是72°
典例分析
O
A
B
C
D
E
F
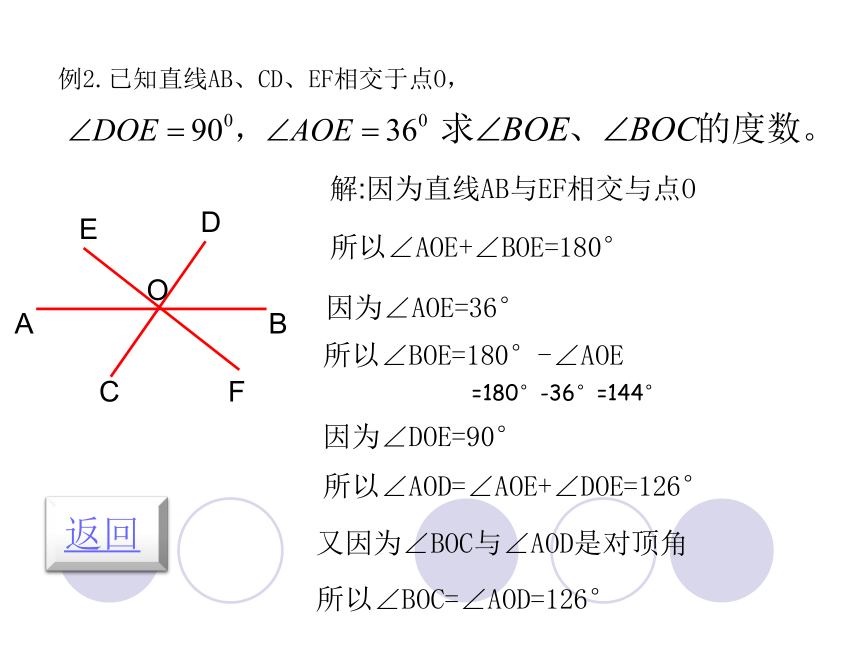
例2.已知直线AB、CD、EF相交于点O,
解:因为直线AB与EF相交与点O
所以∠AOE+∠BOE=180°
因为∠AOE=36°
所以∠BOE=180°-∠AOE
=180°-36°=144°
因为∠DOE=90°
所以∠AOD=∠AOE+∠DOE=126°
又因为∠BOC与∠AOD是对顶角
所以∠BOC=∠AOD=126°
返回
1.垂线的定义: 两条直线相交,所构成的四个角中,有一个角是90°时,就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线。它们的交点叫垂足。
2. 垂线的性质: (1)过一点有且只有一条直线与已知直线垂直。(2): 直线外一点与直线上各点连结的所有线段中,垂线段最短。简称:垂线段最短。
3.点到直线的距离: 从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
4.如遇到线段与线段,线段与射线,射线与射线,线段或射线与直线垂直时,特指它们所在的直线互相垂直。
5.垂线是直线,垂线段特指一条线段是图形,点到直线距离是指垂线段的长度,是指一个数量,是有单位的。
垂 线
下列说法中正确的是( )
A.有且只有一条直线垂直于已知直线。
B.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离。
C.互相垂直的两条直线一定相交。
D.直线c外一点A与直线c上各点连接而成的所有线段中,最短线段的长是3cm,则点A到直线c的距离是3cm。
D
2、“过一点有且只有一条直线与已
知直线垂直”这句话对吗?为什么?
知识及运用
l
P
P
l
直线上、外一点
┓
A
B
C
D
O
E
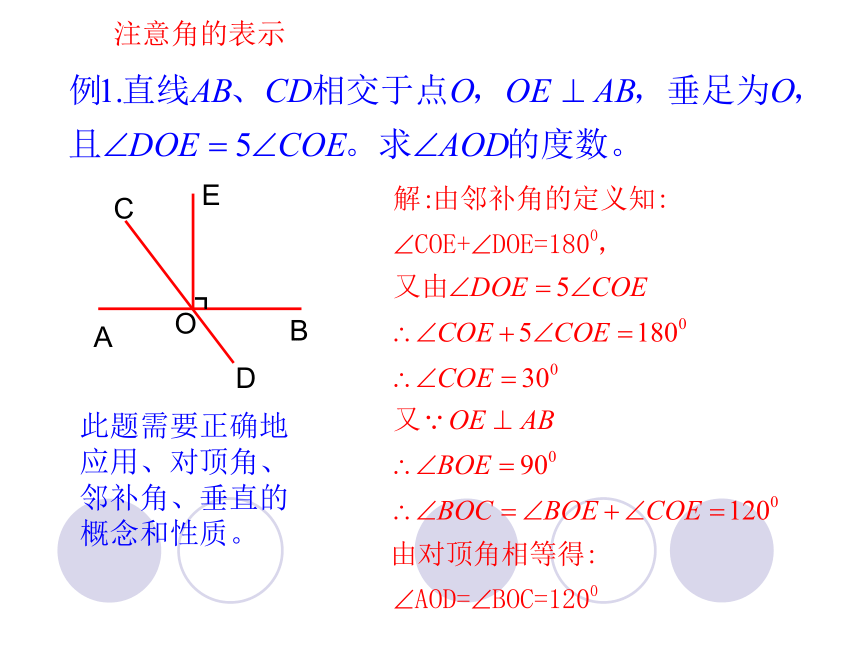
此题需要正确地
应用、对顶角、
邻补角、垂直的
概念和性质。
注意角的表示
O
A
D
C
B
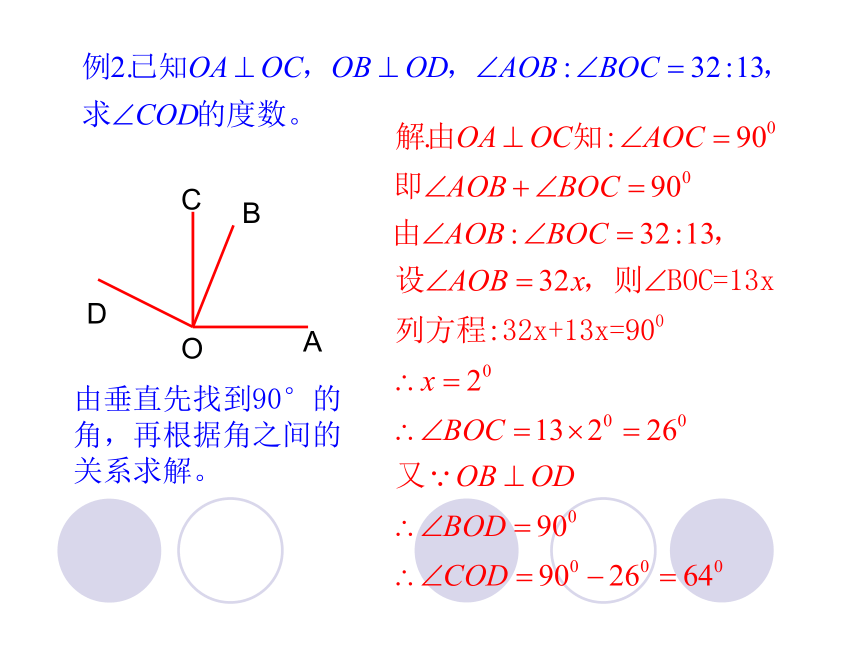
由垂直先找到90°的角,再根据角之间的关系求解。
C
∟
理由:垂线段最短
例3:如图,要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。
A
D
C
B
E
F
例4:你能量出C到AB的距离,B到AC的距离,A到BC的距离吗?
思考:三角形的三条垂线有什么特点?
三角形的三条垂线都交于一点;
锐角三角形的三条垂线交点在三角形的内部;
直角三角形的三条垂线交点在直角顶点;
钝角三角形的三条垂线交点在三角形的外部;
例5:你能画出ABC三点到对边的垂线吗?
平行线的概念:在同一平面内,不相交的两条直线叫做平行线。
2. 两直线的位置关系: 在同一平面内,两直线的位置关系只有两种:(1)相交; (2)平行。
3. 平行线的基本性质:
(1) 平行公理(平行线的存在性和唯一性)
经过直线外一点,有且只有一条直线与已知直线平行。
(2) 推论(平行线的传递性) 如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
4.同位角、内错角、同旁内角的概念
同位角、内错角、同旁内角,指的是一条直线分别与两条直线相交构成的八个角中,不共顶点的角之间的特殊位置关系。它们与对顶角、邻补角一样,总是成对存在着的。
平 行
2、“过一点有且只有一条直线与已
知直线平行”这句话对吗?为什么?
知识及运用
l
P
P
l
直线外一点
如图,AD//BC,AE=BE.
??? (1) 过E作EF//BC交CD于F,过D作DG//AB交BC于G;
??? (2) EF和AD平行吗?为什么?
F
G
注意用虚线,什么时候出头,什么时候不出头
1、同位角的位置特征是:
2、内错角的位置特征是:
3、同旁内角的位置特征是:
(1)在截线的同旁,
(2)在被截两直线的同方向。
(1)在截线的两旁,
(2)在被截两直线之间。
(1)在截线的同旁,
(2)在被截两直线之间。
F
1
3
7
5
2
8
6
D
C
A
B
E
4
被截线
截线
三线八角
∠1和∠2不是同位角,
如图中的∠1和∠2是同位角吗? 为什么?
1
2
1
2
∵∠1和∠2无一边共线。
∠1和∠2是同位角,
∵∠1和∠2有一边共线、同向
且不共顶点。
练 一 练
A
C
B
D
E
1
2
答:∠ EAC
答:∠ DAB
答:∠ BAC,∠BAE , ∠2
∠1与哪个角是同旁内角?
∠2与哪个角是内错角?
例1. ∠1与哪个角是内错角?
(1)定义法;在同一平面内不相交的两条直线是平行线。
(2)传递法;两条直线都和第三条直线平行,这两条直线也平行。
(4)三种角判定(3种方法):
在这六种方法中,定义一般不常用。
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
(3)因为a⊥c, a⊥b;
所以b//c
a
b
C
F
A
B
C
D
E
1
2
3
4
判定两直线平行的方法有三种:
证明: ∵ ∠DAC= ∠ACB (已知)
A
B
C
D
E
F
∴ AD// BC
(内错角相等,两直线平行)
∵ ∠D+∠DFE=180°(已知)
∴ AD// EF
(同旁内角互补,两直线平行)
∴ EF// BC
(平行于同一条直线的两条直线互相平行)
例2. 已知∠DAC= ∠ACB, ∠D+∠DFE=1800,求证:EF//BC
平行线的判定
两直线平行
条件
结论
同位角相等
内错角相等
同旁内角互补
条件
同位角相等
内错角相等
同旁内角互补
结论
两直线平行
夹在两平行线间的垂线段的长度,叫做两平行线间的距离。
平
行
线
的
性
质
证明:由:∠1+∠2=180°(已知)
4
1
2
3
A
B
C
E
F
D
(同旁内角互补,两直线平行)
∠1=∠3(对顶角相等)
∠2=∠4(对顶角相等)
所以∠3+∠4=180°
(等量代换)
AB//CD .
例1. 如图 已知:∠1+∠2=180°,求证:AB∥CD。
证明: ∵由AC∥DE (已知)
A
D
B
E
1
2
C
∴ ∠ACD= ∠2
(两直线平行,内错角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠ACD (等量代换)
∴AB ∥ CD
(内错角相等,两直线平行)
例2. 如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD。
∵ EF⊥AB,CD⊥AB (已知)
∴ AD∥BC
(垂直于同一条直线的两条直线互相平行)
∴ ∠EFB= ∠DCB
(两直线平行,同位角相等)
∵ ∠EFB=∠GDC (已知)
∴ ∠DCB=∠GDC (等量代换)
∴ DG∥BC
(内错角相等,两直线平行)
∴ ∠AGD=∠ACB
(两直线平行,同位角相等)
证明:
例3.已知 EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。
3、如图,AB∥CD,EF分别交AB、
CD于M、N,∠EMB=50°,MG平
分∠BMF,MG交CD于G,求∠1的
度数。
知识及运用
A
B
C
D
E
M
N
F
G
1
∵ MG平分∠BMF(已知)
∴ ∠BMG= ∠BMF
(角平分线定义)
1. 命题的概念: 判断一件事情的句子,叫做命题。
命题必须是一个完整的句子; 这个句子必须对某件事情做出肯定或者否定的判断。两者缺一不可。
2. 命题的组成: 每个命题是由题设、结论两部分组成。
题设是已知事项;结论是由已知事项推出的事项。
命题常写成“如果……,那么……”的形式。或 “若……,则……”等形式。
真命题和假命题: 命题是一个判断,这个判断可能是正确的,也可以是错误的。由此可以把命题分成真命题和假命题。
真命题就是: 如果题设成立,那么结论一定成立的命题。
假命题就是: 如果题设成立时,不能保证结论总是成立的命题。
命 题
画线段AB=2cm
直角都相等;
两条直线相交,有几个交点?
如果两个角不相等,那么这两个角不是对顶角。
相等的角都是直角;
分析: 因为(1)、(3)不是对某一件事作出判断的句子,所以(1)、(3)不是命题。
解. (1)、(3)不是命题; (2)、(4)、(5)是命题; (2)、(4)都是真命,(5)是假命题。
例1. 判断下列语句,是不是命题,如果是命题,是真命题,还是假命题?
“如果两个角是两个等角的余角,那么这两个角相等”。
“把‘等角的余角相等’改写成‘如果……,那么……’的形式是 ”
“同角的补角相等”
“如果两个角是同一个角的补角,那么这两个角相等”。
A
B
C
D
分析: 不妨选择(1)与(2)作条件,由平行性质 “两直线平行,同旁内角互补”可得∠A=∠C,故满足要求。由(1)与(3)也能得出(2)成立,由(2)与(3)也能得出(1)成立。
解: 如果在四边形ABCD中,AB//DC、AD//BC,那么∠A=∠C。
例2. 如图给出下列论断: (1)AB//CD (2)AD//BC (3)∠A=∠C以上,其中两个作为题设,另一个作为结论,用 “如果……,那么……”的形式,写出一个你认为正确的命题。
同一平面内的四条直线满足a⊥b,b⊥c,c⊥d,则下列式子成立的是( )
A.a∥b B.b⊥d
C.a⊥d D.b∥c
C
1. 平移变换的定义: 把一个图形整体沿某一方向移动,会得到
一个新图形,这样的图形运动,叫做平移变换,简称平移。
平移的特征: (1)平移不改变图形的形状和大小。
(2)新图形中的每一点,都是由原图形中的某一点移动后得到
的,这两个点是对应点,对应点连结而成的线段平行且相等。
决定平移的因素是平移的方向和距离。
经过平移,图形上的每一点都沿同一方向移动相同的距离。
经过平移,对应角相等;对应线段平行且相等;
对应点所连的线段平行且相等。
平 移
站在运动着的电梯上的人
左右推动的推拉窗扇
小李荡秋千运动
躺在火车上睡觉的旅客
分析: A、B、D属平移,在一个位置取两点连成一条线,在另一个位置再观察这条线段,发现是平行的,而C同样取两点连成一条线段,运动到另一位置时,可能已不平行
解: 选C
例1. 在以下生活现象中,不是平移现象的是
.下面生活中的物体的运动情况可以看成平移的是 。
(1)摆动的钟摆。
(2)在笔直的公路上行驶的汽车。
(3)随风摆动的旗帜。
(4)摇动的大绳。
(5)汽车玻璃上雨刷的运动。
(6)从楼顶自由落下的球(球不旋转)。
(2)和(6)
例2. 如图所示,△ABC平移到△A′B′C′的位置,则点A的
对应点是____,点B的对应点是____,点C的对应点是____。
线段AB的对应线段是___________,线段BC的对应线段是
______,线段AC的对应线段是_______。∠BAC的对应
角是________,∠ABC的对应角是_________,∠ACB的
对应角是_________。△ABC的平移方向是_____________
___________________________,平移距离是_____________
________________________________。
A
B
C
A′
B′
C′
A′
B′
C′
沿着射线AA′
(或BB′,或CC′)的方向
线段AA′的长
(或线段BB′的长或线段CC′的长
填空题
分辨一下:
(1) (2) (3) (4)
A B C D
A B C D
找出平移后的图片。
(3)
D
B
通过这节课的学习活动,你有什么收获?
课堂小结
小结:
1、邻补角、对顶角的概念和性质
2、垂线画法、垂线段的性质
3、平行线的判定和性质
4、命题的题设与结论以及命题的真假
5、平移的概念和平移的性质
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
学习要有三心,一信心,二决心,三恒心。 —— 陈景润
章末复习
相交线
两条
直线
相交
两条直线被
第三条所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
平行线的判定
平行线的性质
两条平行线的距离
平移
平移的特征
命题
知识构图
知识框图
相交线
两条
直线
相交
两条直线被
第三条所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
平行线的判定
平行线的性质
两条平行线的距离
平移
平移的特征
命题
知识构图
(1)两条直线相交所构成的四个角中,
有公共顶点但没有公共边的两个角是对顶角。
如图(2).
(2)一个角的两边分别是另一个角的两边的反向延长线,这两个角是对顶角。
同角的补角相等。
对顶角相等。
两个特征:(1) 具有公共顶点;
(2) 角的两边互为反向延长线。
n条直线相交于一点,
就有n(n-1)对对顶角。
1
2
(1)
(2)
1
2
3
4
两条直线相交所构成的四了角中,有公共顶点且有一条公共边的两个角是邻补角.如图(1)
1.互为邻补角:
2. 对顶角:
3. 邻补角的性质:
4. 对顶角性质:
巩固旧识
三条直线两两相交于同一点时,对顶角有m对,交于不同三点时,对顶角有n对,则m与n的关系是( )
A.m = n B.m>n
C.m<n D.m + n = 10
A
返回
A
B
C
D
O
在解决与角的计算有关的问题时,经常用到代数方法。
解:设∠AOC=2x°,则∠AOD=3x°
所以2x°+3x°=180°
因为∠AOC+∠AOD=180°
解得x=36°
所以∠AOC=2x=72°
∠BOD=∠AOC=72°
答: ∠BOD的度数是72°
典例分析
O
A
B
C
D
E
F
例2.已知直线AB、CD、EF相交于点O,
解:因为直线AB与EF相交与点O
所以∠AOE+∠BOE=180°
因为∠AOE=36°
所以∠BOE=180°-∠AOE
=180°-36°=144°
因为∠DOE=90°
所以∠AOD=∠AOE+∠DOE=126°
又因为∠BOC与∠AOD是对顶角
所以∠BOC=∠AOD=126°
返回
1.垂线的定义: 两条直线相交,所构成的四个角中,有一个角是90°时,就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线。它们的交点叫垂足。
2. 垂线的性质: (1)过一点有且只有一条直线与已知直线垂直。(2): 直线外一点与直线上各点连结的所有线段中,垂线段最短。简称:垂线段最短。
3.点到直线的距离: 从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
4.如遇到线段与线段,线段与射线,射线与射线,线段或射线与直线垂直时,特指它们所在的直线互相垂直。
5.垂线是直线,垂线段特指一条线段是图形,点到直线距离是指垂线段的长度,是指一个数量,是有单位的。
垂 线
下列说法中正确的是( )
A.有且只有一条直线垂直于已知直线。
B.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离。
C.互相垂直的两条直线一定相交。
D.直线c外一点A与直线c上各点连接而成的所有线段中,最短线段的长是3cm,则点A到直线c的距离是3cm。
D
2、“过一点有且只有一条直线与已
知直线垂直”这句话对吗?为什么?
知识及运用
l
P
P
l
直线上、外一点
┓
A
B
C
D
O
E
此题需要正确地
应用、对顶角、
邻补角、垂直的
概念和性质。
注意角的表示
O
A
D
C
B
由垂直先找到90°的角,再根据角之间的关系求解。
C
∟
理由:垂线段最短
例3:如图,要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。
A
D
C
B
E
F
例4:你能量出C到AB的距离,B到AC的距离,A到BC的距离吗?
思考:三角形的三条垂线有什么特点?
三角形的三条垂线都交于一点;
锐角三角形的三条垂线交点在三角形的内部;
直角三角形的三条垂线交点在直角顶点;
钝角三角形的三条垂线交点在三角形的外部;
例5:你能画出ABC三点到对边的垂线吗?
平行线的概念:在同一平面内,不相交的两条直线叫做平行线。
2. 两直线的位置关系: 在同一平面内,两直线的位置关系只有两种:(1)相交; (2)平行。
3. 平行线的基本性质:
(1) 平行公理(平行线的存在性和唯一性)
经过直线外一点,有且只有一条直线与已知直线平行。
(2) 推论(平行线的传递性) 如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
4.同位角、内错角、同旁内角的概念
同位角、内错角、同旁内角,指的是一条直线分别与两条直线相交构成的八个角中,不共顶点的角之间的特殊位置关系。它们与对顶角、邻补角一样,总是成对存在着的。
平 行
2、“过一点有且只有一条直线与已
知直线平行”这句话对吗?为什么?
知识及运用
l
P
P
l
直线外一点
如图,AD//BC,AE=BE.
??? (1) 过E作EF//BC交CD于F,过D作DG//AB交BC于G;
??? (2) EF和AD平行吗?为什么?
F
G
注意用虚线,什么时候出头,什么时候不出头
1、同位角的位置特征是:
2、内错角的位置特征是:
3、同旁内角的位置特征是:
(1)在截线的同旁,
(2)在被截两直线的同方向。
(1)在截线的两旁,
(2)在被截两直线之间。
(1)在截线的同旁,
(2)在被截两直线之间。
F
1
3
7
5
2
8
6
D
C
A
B
E
4
被截线
截线
三线八角
∠1和∠2不是同位角,
如图中的∠1和∠2是同位角吗? 为什么?
1
2
1
2
∵∠1和∠2无一边共线。
∠1和∠2是同位角,
∵∠1和∠2有一边共线、同向
且不共顶点。
练 一 练
A
C
B
D
E
1
2
答:∠ EAC
答:∠ DAB
答:∠ BAC,∠BAE , ∠2
∠1与哪个角是同旁内角?
∠2与哪个角是内错角?
例1. ∠1与哪个角是内错角?
(1)定义法;在同一平面内不相交的两条直线是平行线。
(2)传递法;两条直线都和第三条直线平行,这两条直线也平行。
(4)三种角判定(3种方法):
在这六种方法中,定义一般不常用。
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
(3)因为a⊥c, a⊥b;
所以b//c
a
b
C
F
A
B
C
D
E
1
2
3
4
判定两直线平行的方法有三种:
证明: ∵ ∠DAC= ∠ACB (已知)
A
B
C
D
E
F
∴ AD// BC
(内错角相等,两直线平行)
∵ ∠D+∠DFE=180°(已知)
∴ AD// EF
(同旁内角互补,两直线平行)
∴ EF// BC
(平行于同一条直线的两条直线互相平行)
例2. 已知∠DAC= ∠ACB, ∠D+∠DFE=1800,求证:EF//BC
平行线的判定
两直线平行
条件
结论
同位角相等
内错角相等
同旁内角互补
条件
同位角相等
内错角相等
同旁内角互补
结论
两直线平行
夹在两平行线间的垂线段的长度,叫做两平行线间的距离。
平
行
线
的
性
质
证明:由:∠1+∠2=180°(已知)
4
1
2
3
A
B
C
E
F
D
(同旁内角互补,两直线平行)
∠1=∠3(对顶角相等)
∠2=∠4(对顶角相等)
所以∠3+∠4=180°
(等量代换)
AB//CD .
例1. 如图 已知:∠1+∠2=180°,求证:AB∥CD。
证明: ∵由AC∥DE (已知)
A
D
B
E
1
2
C
∴ ∠ACD= ∠2
(两直线平行,内错角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠ACD (等量代换)
∴AB ∥ CD
(内错角相等,两直线平行)
例2. 如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD。
∵ EF⊥AB,CD⊥AB (已知)
∴ AD∥BC
(垂直于同一条直线的两条直线互相平行)
∴ ∠EFB= ∠DCB
(两直线平行,同位角相等)
∵ ∠EFB=∠GDC (已知)
∴ ∠DCB=∠GDC (等量代换)
∴ DG∥BC
(内错角相等,两直线平行)
∴ ∠AGD=∠ACB
(两直线平行,同位角相等)
证明:
例3.已知 EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。
3、如图,AB∥CD,EF分别交AB、
CD于M、N,∠EMB=50°,MG平
分∠BMF,MG交CD于G,求∠1的
度数。
知识及运用
A
B
C
D
E
M
N
F
G
1
∵ MG平分∠BMF(已知)
∴ ∠BMG= ∠BMF
(角平分线定义)
1. 命题的概念: 判断一件事情的句子,叫做命题。
命题必须是一个完整的句子; 这个句子必须对某件事情做出肯定或者否定的判断。两者缺一不可。
2. 命题的组成: 每个命题是由题设、结论两部分组成。
题设是已知事项;结论是由已知事项推出的事项。
命题常写成“如果……,那么……”的形式。或 “若……,则……”等形式。
真命题和假命题: 命题是一个判断,这个判断可能是正确的,也可以是错误的。由此可以把命题分成真命题和假命题。
真命题就是: 如果题设成立,那么结论一定成立的命题。
假命题就是: 如果题设成立时,不能保证结论总是成立的命题。
命 题
画线段AB=2cm
直角都相等;
两条直线相交,有几个交点?
如果两个角不相等,那么这两个角不是对顶角。
相等的角都是直角;
分析: 因为(1)、(3)不是对某一件事作出判断的句子,所以(1)、(3)不是命题。
解. (1)、(3)不是命题; (2)、(4)、(5)是命题; (2)、(4)都是真命,(5)是假命题。
例1. 判断下列语句,是不是命题,如果是命题,是真命题,还是假命题?
“如果两个角是两个等角的余角,那么这两个角相等”。
“把‘等角的余角相等’改写成‘如果……,那么……’的形式是 ”
“同角的补角相等”
“如果两个角是同一个角的补角,那么这两个角相等”。
A
B
C
D
分析: 不妨选择(1)与(2)作条件,由平行性质 “两直线平行,同旁内角互补”可得∠A=∠C,故满足要求。由(1)与(3)也能得出(2)成立,由(2)与(3)也能得出(1)成立。
解: 如果在四边形ABCD中,AB//DC、AD//BC,那么∠A=∠C。
例2. 如图给出下列论断: (1)AB//CD (2)AD//BC (3)∠A=∠C以上,其中两个作为题设,另一个作为结论,用 “如果……,那么……”的形式,写出一个你认为正确的命题。
同一平面内的四条直线满足a⊥b,b⊥c,c⊥d,则下列式子成立的是( )
A.a∥b B.b⊥d
C.a⊥d D.b∥c
C
1. 平移变换的定义: 把一个图形整体沿某一方向移动,会得到
一个新图形,这样的图形运动,叫做平移变换,简称平移。
平移的特征: (1)平移不改变图形的形状和大小。
(2)新图形中的每一点,都是由原图形中的某一点移动后得到
的,这两个点是对应点,对应点连结而成的线段平行且相等。
决定平移的因素是平移的方向和距离。
经过平移,图形上的每一点都沿同一方向移动相同的距离。
经过平移,对应角相等;对应线段平行且相等;
对应点所连的线段平行且相等。
平 移
站在运动着的电梯上的人
左右推动的推拉窗扇
小李荡秋千运动
躺在火车上睡觉的旅客
分析: A、B、D属平移,在一个位置取两点连成一条线,在另一个位置再观察这条线段,发现是平行的,而C同样取两点连成一条线段,运动到另一位置时,可能已不平行
解: 选C
例1. 在以下生活现象中,不是平移现象的是
.下面生活中的物体的运动情况可以看成平移的是 。
(1)摆动的钟摆。
(2)在笔直的公路上行驶的汽车。
(3)随风摆动的旗帜。
(4)摇动的大绳。
(5)汽车玻璃上雨刷的运动。
(6)从楼顶自由落下的球(球不旋转)。
(2)和(6)
例2. 如图所示,△ABC平移到△A′B′C′的位置,则点A的
对应点是____,点B的对应点是____,点C的对应点是____。
线段AB的对应线段是___________,线段BC的对应线段是
______,线段AC的对应线段是_______。∠BAC的对应
角是________,∠ABC的对应角是_________,∠ACB的
对应角是_________。△ABC的平移方向是_____________
___________________________,平移距离是_____________
________________________________。
A
B
C
A′
B′
C′
A′
B′
C′
沿着射线AA′
(或BB′,或CC′)的方向
线段AA′的长
(或线段BB′的长或线段CC′的长
填空题
分辨一下:
(1) (2) (3) (4)
A B C D
A B C D
找出平移后的图片。
(3)
D
B
通过这节课的学习活动,你有什么收获?
课堂小结
小结:
1、邻补角、对顶角的概念和性质
2、垂线画法、垂线段的性质
3、平行线的判定和性质
4、命题的题设与结论以及命题的真假
5、平移的概念和平移的性质
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
学习要有三心,一信心,二决心,三恒心。 —— 陈景润
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
