2020春北师大版七年级数学下2.1 两条直线的位置关系同步练习含答案
文档属性
| 名称 | 2020春北师大版七年级数学下2.1 两条直线的位置关系同步练习含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 134.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览



文档简介
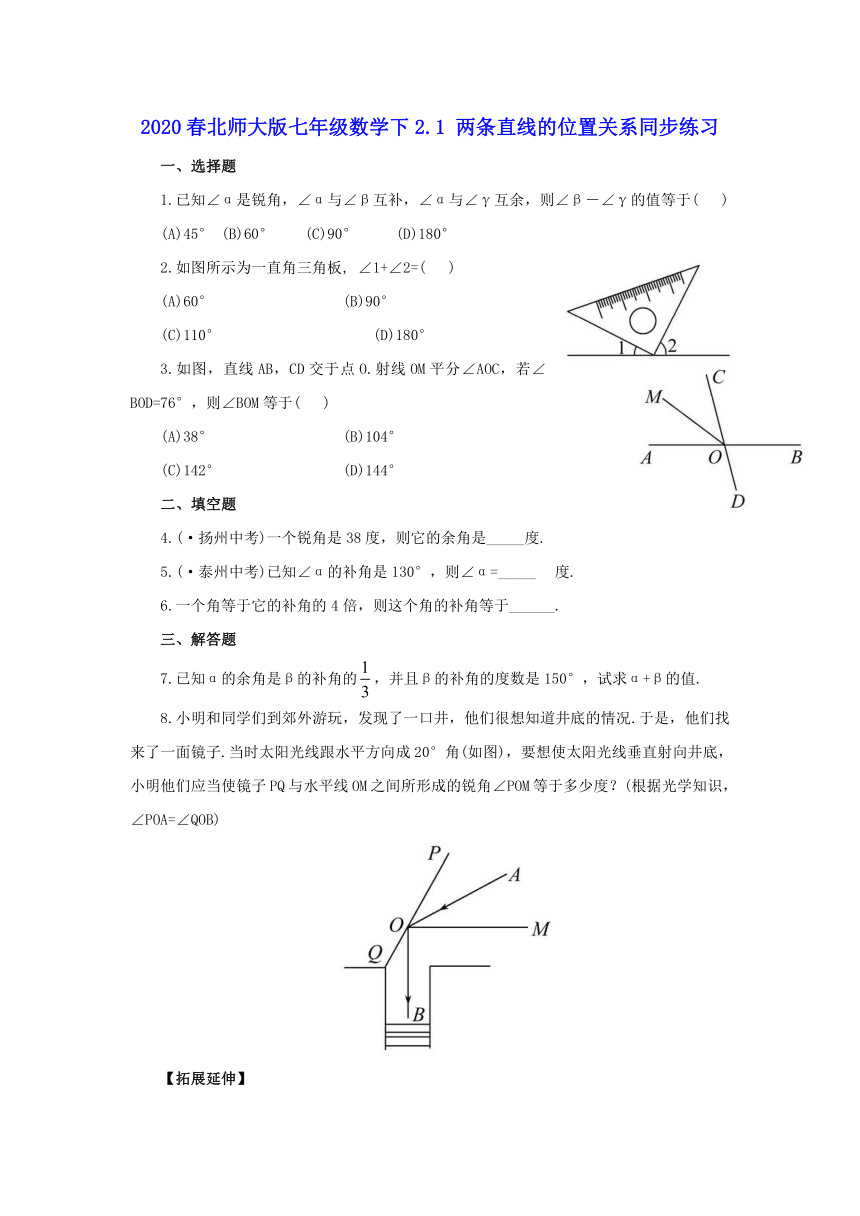
2020春北师大版七年级数学下2.1 两条直线的位置关系同步练习
一、选择题
1.已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β-∠γ的值等于( )
(A)45° (B)60° (C)90° (D)180°
2.如图所示为一直角三角板, ∠1+∠2=( )
(A)60° (B)90°
(C)110° (D)180°
3.如图,直线AB,CD交于点O.射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于( )
(A)38° (B)104°
(C)142° (D)144°
二、填空题
4.(·扬州中考)一个锐角是38度,则它的余角是_____度.
5.(·泰州中考)已知∠α的补角是130°,则∠α=_____ 度.
6.一个角等于它的补角的4倍,则这个角的补角等于______.
三、解答题
7.已知α的余角是β的补角的,并且β的补角的度数是150°,试求α+β的值.
8.小明和同学们到郊外游玩,发现了一口井,他们很想知道井底的情况.于是,他们找来了一面镜子.当时太阳光线跟水平方向成20°角(如图),要想使太阳光线垂直射向井底,小明他们应当使镜子PQ与水平线OM之间所形成的锐角∠POM等于多少度?(根据光学知识,∠POA=∠QOB)
【拓展延伸】
9.如图,∠AOC与∠EOC有公共顶点O,OC是它们的公共边,它们的另一条边OA与OE互为反向延长线.我们把这样的两个角叫做邻补角.
(1)试再写出图中的一对邻补角.
(2)邻补角一定互补吗?互补的两个角一定是邻补角吗?为什么?
(3)如果OB,OD分别是∠AOC与∠EOC的平分线,那么OB与OD之间有何关系?
试说明理由.
答案解析
1.【解析】选C.由题意,得∠α+∠β=180°,∠α+∠γ=90°,两式相减得
∠β-∠γ=90°.故选C.
2.【解析】选B.根据平角的定义可得,∠1+90°+∠2=180°,所以∠1+∠2=90°.
3.【解析】选C.因为∠BOD=76°,∠AOC与∠BOD是对顶角,所以∠AOC=76°,又因为∠BOC与∠AOC互补,所以∠BOC=104°,又因为OM平 分∠AOC, 所以
∠COM=38°,所以∠BOM=142°.
4.【解析】因为这个角是38度,所以这个角的余角为90-38=52(度).
答案:52
5.【解析】因为∠α的补角是130°,所以∠α=180°-130°=50°.
答案:50
6.【解析】设这个角的度数为x°,则它的补角为(180-x)°,根据题意列方程得:x=4(180-x),解得x=144,所以这个角的补角等于180°-144°=36°.
答案:36°
7.【解析】因为β的补角的度数是150°,所以β=180°-150°=30°,所以
α=90°-×150°=40°,所以α+β=40°+30°=70°.
【归纳整合】本题主要考查互为余角与互为补角的概念,首先要弄清楚题目中一共涉及几个角,除了要求的角外,还有余角和补角;其次将其表示出来;最后根据等量关系求解.
8.【解析】由题意知∠BOM= 90°,∠AOM= 20°,
又因为∠POA+∠QOB +∠BOM +∠AOM= 180°.
∠POA=∠QOB,
所以∠POA=∠QOB==35°,
所以∠POM=∠POA +∠AOM=55°.
9.【解析】(1)∠AOB与∠EOB或∠AOD与∠EOD.
(2)邻补角一定互补,互补的两个角不一定是邻补角,因为互补的角不一定有共同的顶点.
(3)垂直.因为∠BOC=∠AOC ,∠DOC =∠EOC,∠AOC+∠EOC=180°,
所以∠BOC+∠DOC=(∠AOC +∠EOC)=90°,
所以OB与OD垂直.
《2.1 两条直线的位置关系》同步练习2
一、选择题
1.下列语句说法正确的个数是( )
①两条直线相交成四个角,如果有两个角相等,那么这两条直线垂直;
②两条直线相交成四个角,如果有一个角是直角,那么这两条直线垂直;
③一条直线的垂线可以画无数条;
④在同一平面内, 经过一个已知点能画一条且只能画一条直线和已知直线垂直.
(A)1个 (B)2个 (C)3个 (D)4个
2.点P为直线l外一点,点A,B,C为直线l上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线l的距离为( )
(A)4 cm (B)2 cm
(C)小于2 cm (D)不大于2 cm
3.如图,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为( )
(A)120° (B)130°
(C)135° (D)140°
二、填空题
4.如图,已知∠AOB=∠COD=90°,∠AOD=150°,则∠BOC=______.
5.如图,OA⊥OC于O,直线BD过点O,∠AOB=40°,则∠COD等于_____.
6.如图,OC⊥OA,OB⊥OD,O为垂足,若∠BOC=35°,则∠AOD=_____.
三、解答题
7.(8分)如图,OA⊥OB,OC⊥OD,OE是OD的反向延长线.
(1)试说明∠AOC=∠BOD.
(2)若∠BOD=50°,求∠AOE.
8.(8分)如图,O为直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数.
(2)试判断OD与AB的位置关系.
【拓展延伸】
9.(10分)如图,已知A,O,E三点在一条直线上,OB平分∠AOC,∠AOB+∠DOE=
90°,试问:∠COD与∠DOE之间有怎样的关系?说明理由.
答案解析
1.【解析】选C.两条直线相交成四个角,对顶角一定相等,故①错误.如果有一个角是直角,那么这两条直线垂直,所以②正确.一条直线的垂线可以画无数条;在同一平面内, 经过一个已知点能画一条且只能画一条直线和已知直线垂直.所以③④正确.故选C.
2.【解析】选D.由题意知,PC3.【解析】选C.根据垂直的定义,直线EO⊥CD,所以∠EOD=90°,再由角平分线的定义得∠AOD=45°,所以∠BOD=180°-45°=135°.
4.【解析】∠BOC=360°-∠AOB-∠COD-∠AOD=360°-90°-90°-150°=30°.
答案:30°
5.【解析】因为OA⊥OC,所以∠AOC=90°,因为∠AOB=40°,所以∠BOC=50°,所以∠COD=130°.
答案:130°
6.【解析】因为OC⊥OA,OB⊥OD,
所以∠AOB+∠BOC=90°,∠COD+∠BOC=90°,
所以∠AOB+2∠BOC+∠COD=180°,
即∠AOD+∠BOC=180°,
因为∠BOC=35°,
所以∠AOD=145°.
答案:145°
7.【解析】(1)因为OA⊥OB,OC⊥OD,OE是OD的反向延长线,所以∠AOB=90°,∠COD=∠COE=90°.因为∠AOC=∠AOB-∠BOC=90°-∠BOC, ∠BOD=∠COD-
∠BOC=90°-∠BOC,所以∠AOC=∠BOD.
(2)因为∠BOD=50°,由(1)知,∠AOC=∠BOD=50°,所以∠AOE=∠COE-∠AOC=
90°-50°=40°.
8.【解析】(1)因为∠AOC=∠BOC,∠AOC与∠BOC互补,所以∠AOC+∠BOC=
∠AOC+3∠AOC=180°,所以∠AOC=45°,又因为OC是∠AOD的平分线,所以
∠COD=∠AOC=45°.
(2)由(1)得∠COD=∠AOC=45°,所以∠AOD=∠COD+∠AOC=90°,所以OD与AB互相垂直.
9.【解析】相等.因为∠AOB+∠DOE=90°,所以∠BOD=180°-(∠AOB+∠DOE)=
180°-90°=90°,又因为OB平分∠AOC,所以∠AOB=∠BOC,又∠AOB+∠DOE=
90°,∠BOC+∠COD=90°,由等角的余角相等,可得∠COD与∠DOE相等.
一、选择题
1.已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β-∠γ的值等于( )
(A)45° (B)60° (C)90° (D)180°
2.如图所示为一直角三角板, ∠1+∠2=( )
(A)60° (B)90°
(C)110° (D)180°
3.如图,直线AB,CD交于点O.射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于( )
(A)38° (B)104°
(C)142° (D)144°
二、填空题
4.(·扬州中考)一个锐角是38度,则它的余角是_____度.
5.(·泰州中考)已知∠α的补角是130°,则∠α=_____ 度.
6.一个角等于它的补角的4倍,则这个角的补角等于______.
三、解答题
7.已知α的余角是β的补角的,并且β的补角的度数是150°,试求α+β的值.
8.小明和同学们到郊外游玩,发现了一口井,他们很想知道井底的情况.于是,他们找来了一面镜子.当时太阳光线跟水平方向成20°角(如图),要想使太阳光线垂直射向井底,小明他们应当使镜子PQ与水平线OM之间所形成的锐角∠POM等于多少度?(根据光学知识,∠POA=∠QOB)
【拓展延伸】
9.如图,∠AOC与∠EOC有公共顶点O,OC是它们的公共边,它们的另一条边OA与OE互为反向延长线.我们把这样的两个角叫做邻补角.
(1)试再写出图中的一对邻补角.
(2)邻补角一定互补吗?互补的两个角一定是邻补角吗?为什么?
(3)如果OB,OD分别是∠AOC与∠EOC的平分线,那么OB与OD之间有何关系?
试说明理由.
答案解析
1.【解析】选C.由题意,得∠α+∠β=180°,∠α+∠γ=90°,两式相减得
∠β-∠γ=90°.故选C.
2.【解析】选B.根据平角的定义可得,∠1+90°+∠2=180°,所以∠1+∠2=90°.
3.【解析】选C.因为∠BOD=76°,∠AOC与∠BOD是对顶角,所以∠AOC=76°,又因为∠BOC与∠AOC互补,所以∠BOC=104°,又因为OM平 分∠AOC, 所以
∠COM=38°,所以∠BOM=142°.
4.【解析】因为这个角是38度,所以这个角的余角为90-38=52(度).
答案:52
5.【解析】因为∠α的补角是130°,所以∠α=180°-130°=50°.
答案:50
6.【解析】设这个角的度数为x°,则它的补角为(180-x)°,根据题意列方程得:x=4(180-x),解得x=144,所以这个角的补角等于180°-144°=36°.
答案:36°
7.【解析】因为β的补角的度数是150°,所以β=180°-150°=30°,所以
α=90°-×150°=40°,所以α+β=40°+30°=70°.
【归纳整合】本题主要考查互为余角与互为补角的概念,首先要弄清楚题目中一共涉及几个角,除了要求的角外,还有余角和补角;其次将其表示出来;最后根据等量关系求解.
8.【解析】由题意知∠BOM= 90°,∠AOM= 20°,
又因为∠POA+∠QOB +∠BOM +∠AOM= 180°.
∠POA=∠QOB,
所以∠POA=∠QOB==35°,
所以∠POM=∠POA +∠AOM=55°.
9.【解析】(1)∠AOB与∠EOB或∠AOD与∠EOD.
(2)邻补角一定互补,互补的两个角不一定是邻补角,因为互补的角不一定有共同的顶点.
(3)垂直.因为∠BOC=∠AOC ,∠DOC =∠EOC,∠AOC+∠EOC=180°,
所以∠BOC+∠DOC=(∠AOC +∠EOC)=90°,
所以OB与OD垂直.
《2.1 两条直线的位置关系》同步练习2
一、选择题
1.下列语句说法正确的个数是( )
①两条直线相交成四个角,如果有两个角相等,那么这两条直线垂直;
②两条直线相交成四个角,如果有一个角是直角,那么这两条直线垂直;
③一条直线的垂线可以画无数条;
④在同一平面内, 经过一个已知点能画一条且只能画一条直线和已知直线垂直.
(A)1个 (B)2个 (C)3个 (D)4个
2.点P为直线l外一点,点A,B,C为直线l上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线l的距离为( )
(A)4 cm (B)2 cm
(C)小于2 cm (D)不大于2 cm
3.如图,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为( )
(A)120° (B)130°
(C)135° (D)140°
二、填空题
4.如图,已知∠AOB=∠COD=90°,∠AOD=150°,则∠BOC=______.
5.如图,OA⊥OC于O,直线BD过点O,∠AOB=40°,则∠COD等于_____.
6.如图,OC⊥OA,OB⊥OD,O为垂足,若∠BOC=35°,则∠AOD=_____.
三、解答题
7.(8分)如图,OA⊥OB,OC⊥OD,OE是OD的反向延长线.
(1)试说明∠AOC=∠BOD.
(2)若∠BOD=50°,求∠AOE.
8.(8分)如图,O为直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数.
(2)试判断OD与AB的位置关系.
【拓展延伸】
9.(10分)如图,已知A,O,E三点在一条直线上,OB平分∠AOC,∠AOB+∠DOE=
90°,试问:∠COD与∠DOE之间有怎样的关系?说明理由.
答案解析
1.【解析】选C.两条直线相交成四个角,对顶角一定相等,故①错误.如果有一个角是直角,那么这两条直线垂直,所以②正确.一条直线的垂线可以画无数条;在同一平面内, 经过一个已知点能画一条且只能画一条直线和已知直线垂直.所以③④正确.故选C.
2.【解析】选D.由题意知,PC
4.【解析】∠BOC=360°-∠AOB-∠COD-∠AOD=360°-90°-90°-150°=30°.
答案:30°
5.【解析】因为OA⊥OC,所以∠AOC=90°,因为∠AOB=40°,所以∠BOC=50°,所以∠COD=130°.
答案:130°
6.【解析】因为OC⊥OA,OB⊥OD,
所以∠AOB+∠BOC=90°,∠COD+∠BOC=90°,
所以∠AOB+2∠BOC+∠COD=180°,
即∠AOD+∠BOC=180°,
因为∠BOC=35°,
所以∠AOD=145°.
答案:145°
7.【解析】(1)因为OA⊥OB,OC⊥OD,OE是OD的反向延长线,所以∠AOB=90°,∠COD=∠COE=90°.因为∠AOC=∠AOB-∠BOC=90°-∠BOC, ∠BOD=∠COD-
∠BOC=90°-∠BOC,所以∠AOC=∠BOD.
(2)因为∠BOD=50°,由(1)知,∠AOC=∠BOD=50°,所以∠AOE=∠COE-∠AOC=
90°-50°=40°.
8.【解析】(1)因为∠AOC=∠BOC,∠AOC与∠BOC互补,所以∠AOC+∠BOC=
∠AOC+3∠AOC=180°,所以∠AOC=45°,又因为OC是∠AOD的平分线,所以
∠COD=∠AOC=45°.
(2)由(1)得∠COD=∠AOC=45°,所以∠AOD=∠COD+∠AOC=90°,所以OD与AB互相垂直.
9.【解析】相等.因为∠AOB+∠DOE=90°,所以∠BOD=180°-(∠AOB+∠DOE)=
180°-90°=90°,又因为OB平分∠AOC,所以∠AOB=∠BOC,又∠AOB+∠DOE=
90°,∠BOC+∠COD=90°,由等角的余角相等,可得∠COD与∠DOE相等.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
