人教版高中数学必修4课件:1.4.3正切函数的性质和图象(共28张PPT)
文档属性
| 名称 | 人教版高中数学必修4课件:1.4.3正切函数的性质和图象(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
1.4.3正切函的
性质和图象
人教版高中数学必修四
教学目标
1.了解正切函数图像的几何画法
2.掌握正切函数的性质
3.能应用正切函数的图像和性质解决问题
重、难点:
正切函数的图像及性质
一、引入
如何用正弦线作正弦函数图象呢?
用正切线作正切函数y=tanx的图象
类 比
问题1、正切函数 是否为周期函数?
∴ 是周期函数, 是它的一个周期.
想一想:先作哪个周期上的图象好呢?
为什么?
二、自主学习 :探究用正切线作正切函数图象
A
T
0
X
Y
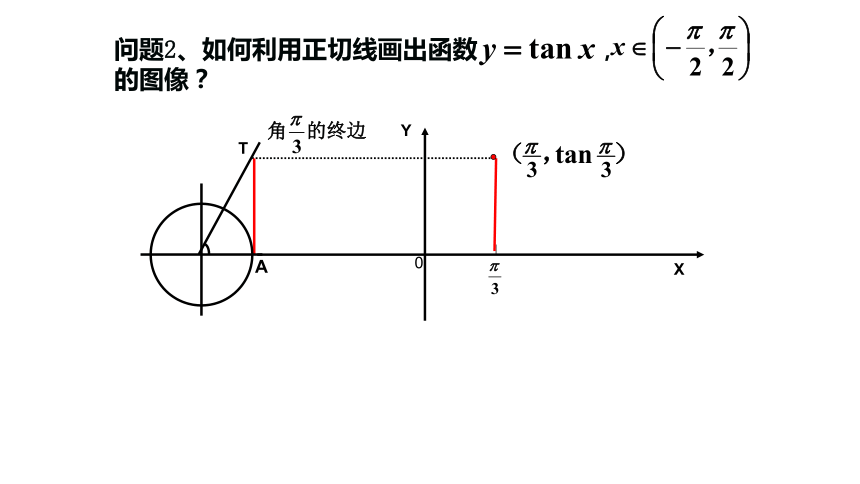
问题2、如何利用正切线画出函数 , 的图像?
作法:
(1) 等分:
(2) 作正切线
(3) 平移
(4) 连线
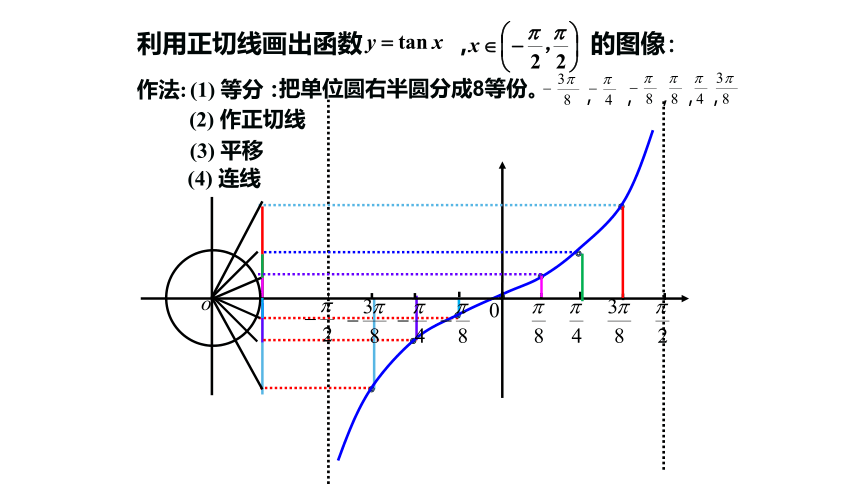
把单位圆右半圆分成8等份。
,
,
,
,
,
利用正切线画出函数 , 的图像:
利用正切函数的周期性,把图象向左,右扩展,得到正切函数
叫做正切曲线.
正切曲线是被相互平行的直线
所隔开的无穷多支曲线组成的.
x
y
0
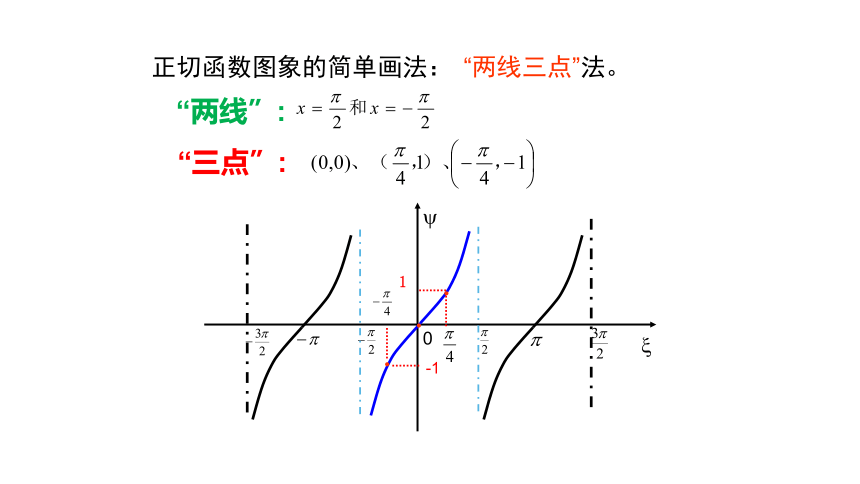
正切函数图象的简单画法:
“两线三点”法。
“三点”:
“两线”:
x
y
0
●
●
●
1
-1
y
x
1
-1
?
-?
0
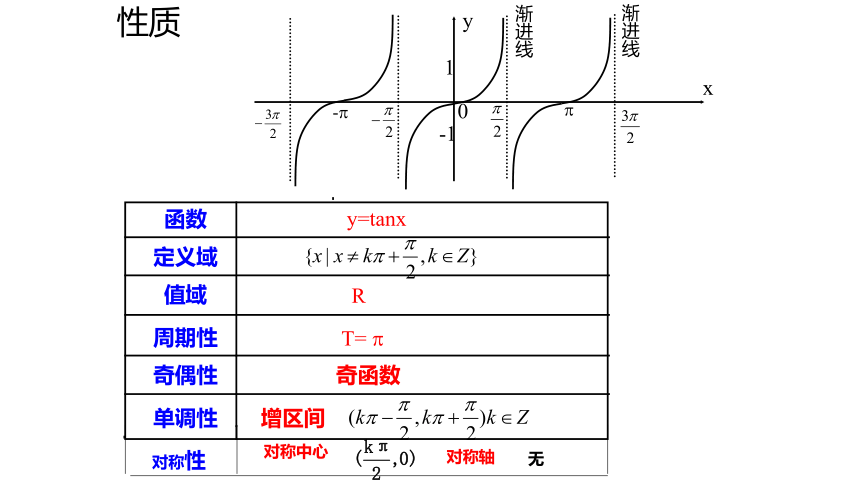
定义域
值域
周期性
奇偶性
单调性
R
T= ?
奇函数
函数
y=tanx
增区间
性质
对称性
对称中心
对称轴
渐进线
渐进线
无
(1)正切函数是整个定义域上的增函数吗?为什么?
(2)正切函数会不会在某一区间内是减函数?为什么?
问题:
A
B
在每一个开区间 ,内都是增函数。
A.是奇函数
B.在整个定义域上是增函数
C.在定义域内无最大值和最小值
D.平行于 轴的的直线被正切曲线各支所截线段相等
1.关于正切函数 , 下列判断不正确的是( )
基础练习
B
例1 求函数 的定义域
由
可得:
所以函数 的定义域是:
解:
求函数
的定义域
练一练
整体代换
求函数 的周期.
所以函数 的周期是
例2
反馈练习:求下列函数的周期:
解:
你能得到函数 的周期吗?
例3 比较下列各组中两个正切函数值的大小
与
解:
在 上是增函数
又
且 是增函数
解:
又
利用单调性
PS:要把两个角放在同一个单调区间上
与
练习:比较大小:
<
>
例4 求下列函数的单调区间:
换元思想
这个题目应该注意什么
函数 的一个对称中心是( )
A . B. C. D.
C
例 5
例6
x
y
0
解:
观察正切曲线,写出满足条件的 的取值范围
探究:
解:
解法1
解法2
y
x
T
A
0
解:
0
y
x
解法1
解法2
反馈演练
答案: 1.
2.
3.
解 :
值域 : R
例 7
( 0 )
正切函数的图像和性质
定义域
值域
周期
奇偶性
单调增区间
对称中心
渐近线方程
奇函数
小结
Z
k
,
k
2
x
?
p
+
p
?
,
自我小结
谈谈本节课你的收获是什么?
哪部分知识掌握的比较好?
还有什么不清楚的细节吗?………
作业
1.课本 P46,6,7,8,9.
2.用列表的方式归纳总结正弦、 余弦、正切函数的图像和性质
TRANSITION PAGE
TRANSITION PAGE
Elements Page
There are more donkeys available online at Animation Factory
1.4.3正切函的
性质和图象
人教版高中数学必修四
教学目标
1.了解正切函数图像的几何画法
2.掌握正切函数的性质
3.能应用正切函数的图像和性质解决问题
重、难点:
正切函数的图像及性质
一、引入
如何用正弦线作正弦函数图象呢?
用正切线作正切函数y=tanx的图象
类 比
问题1、正切函数 是否为周期函数?
∴ 是周期函数, 是它的一个周期.
想一想:先作哪个周期上的图象好呢?
为什么?
二、自主学习 :探究用正切线作正切函数图象
A
T
0
X
Y
问题2、如何利用正切线画出函数 , 的图像?
作法:
(1) 等分:
(2) 作正切线
(3) 平移
(4) 连线
把单位圆右半圆分成8等份。
,
,
,
,
,
利用正切线画出函数 , 的图像:
利用正切函数的周期性,把图象向左,右扩展,得到正切函数
叫做正切曲线.
正切曲线是被相互平行的直线
所隔开的无穷多支曲线组成的.
x
y
0
正切函数图象的简单画法:
“两线三点”法。
“三点”:
“两线”:
x
y
0
●
●
●
1
-1
y
x
1
-1
?
-?
0
定义域
值域
周期性
奇偶性
单调性
R
T= ?
奇函数
函数
y=tanx
增区间
性质
对称性
对称中心
对称轴
渐进线
渐进线
无
(1)正切函数是整个定义域上的增函数吗?为什么?
(2)正切函数会不会在某一区间内是减函数?为什么?
问题:
A
B
在每一个开区间 ,内都是增函数。
A.是奇函数
B.在整个定义域上是增函数
C.在定义域内无最大值和最小值
D.平行于 轴的的直线被正切曲线各支所截线段相等
1.关于正切函数 , 下列判断不正确的是( )
基础练习
B
例1 求函数 的定义域
由
可得:
所以函数 的定义域是:
解:
求函数
的定义域
练一练
整体代换
求函数 的周期.
所以函数 的周期是
例2
反馈练习:求下列函数的周期:
解:
你能得到函数 的周期吗?
例3 比较下列各组中两个正切函数值的大小
与
解:
在 上是增函数
又
且 是增函数
解:
又
利用单调性
PS:要把两个角放在同一个单调区间上
与
练习:比较大小:
<
>
例4 求下列函数的单调区间:
换元思想
这个题目应该注意什么
函数 的一个对称中心是( )
A . B. C. D.
C
例 5
例6
x
y
0
解:
观察正切曲线,写出满足条件的 的取值范围
探究:
解:
解法1
解法2
y
x
T
A
0
解:
0
y
x
解法1
解法2
反馈演练
答案: 1.
2.
3.
解 :
值域 : R
例 7
( 0 )
正切函数的图像和性质
定义域
值域
周期
奇偶性
单调增区间
对称中心
渐近线方程
奇函数
小结
Z
k
,
k
2
x
?
p
+
p
?
,
自我小结
谈谈本节课你的收获是什么?
哪部分知识掌握的比较好?
还有什么不清楚的细节吗?………
作业
1.课本 P46,6,7,8,9.
2.用列表的方式归纳总结正弦、 余弦、正切函数的图像和性质
TRANSITION PAGE
TRANSITION PAGE
Elements Page
There are more donkeys available online at Animation Factory
