人教A版高中数学必修四课件:1.5 三角函数图像平移伸缩变换(共22张PPT)
文档属性
| 名称 | 人教A版高中数学必修四课件:1.5 三角函数图像平移伸缩变换(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 246.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
函数 的图像
1.5 三角函数图像平移伸缩变换
人教版高中数学必修四
y=sinx
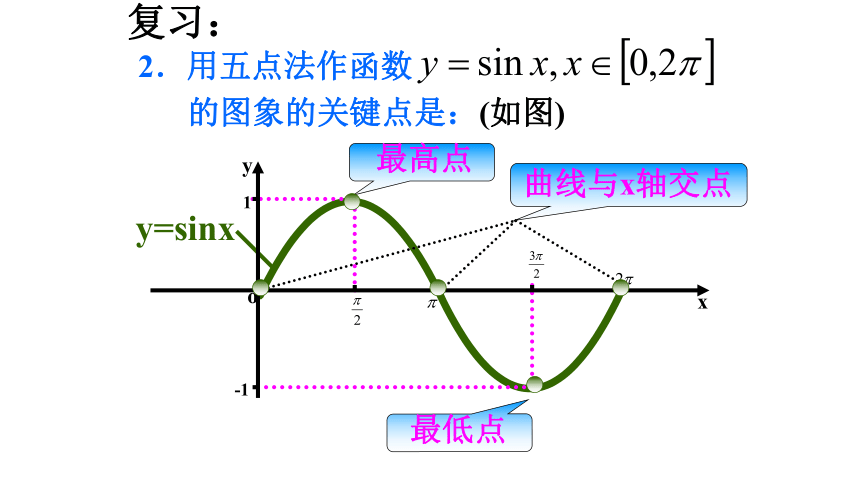
最高点
曲线与x轴交点
-1
1
o
y
x
的图象的关键点是:(如图)
最低点
复习:
2.用五点法作函数
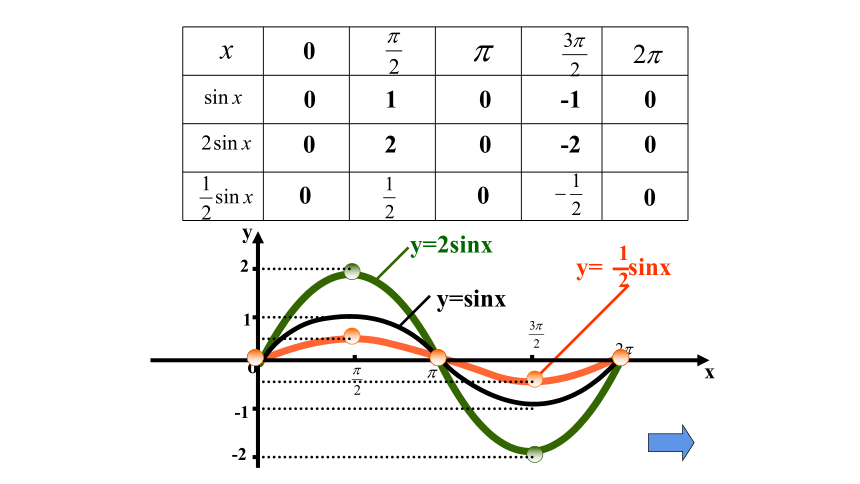
在同一坐标系中作出y=2sinx及 y= sinx的简图,并指出它们与y=sinx图象间的关系.
1
2
问题1
新课:
y=2sinx
y=sinx
y= sinx
1
2
x
2
-2
-1
1
o
y
0
0
0
0
0 1 0 -1 0
0 2 0 -2 0
可以看作把正弦曲线上所有点的纵坐标伸长(当A>1时)或缩短(当0小结1
(其中
且
)
函数
的图象
函数
的值域是
A的作用 纵向伸缩
改变
引起值域
问题2
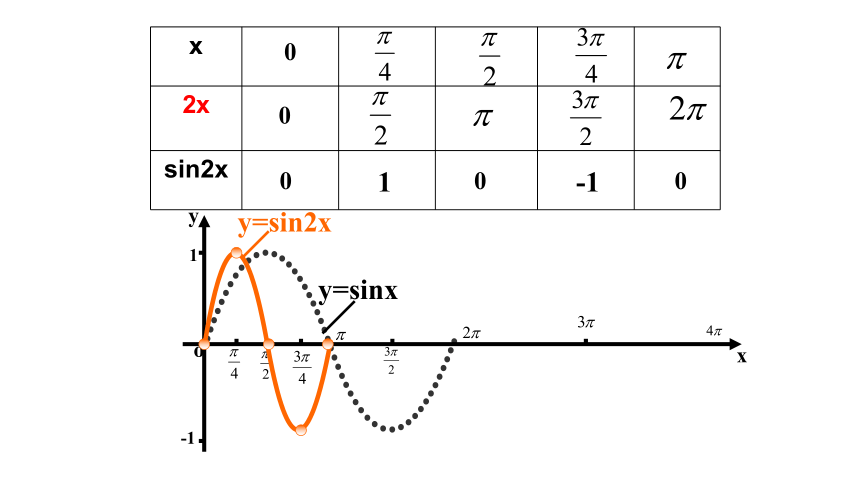
在同一坐标系中作出函数y=sin2x及y=sin x的简图,并指出它们y=sinx图象间的关系。
1
2
x
2x
sin2x
x
-1
1
o
y
0
0
y=sinx
y=sin2x
0 0 0
1
-1
x
-1
1
o
y
x
x
sin x
0 2
0
0 1 0 -1 0
1
2
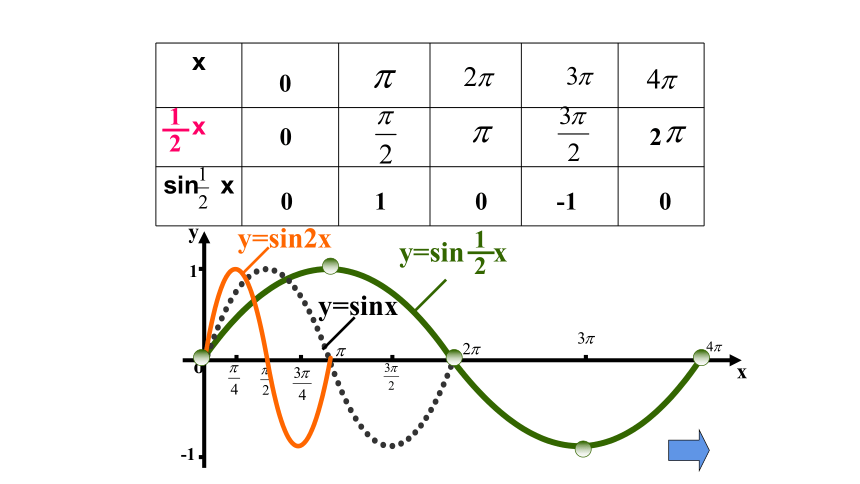
y=sin x
1
2
y=sinx
y=sin2x
小结2
(其中
且
)
函数
的图象
可以看作把正弦曲线上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时)到原来的 倍(纵坐标不变)而得到.
T= 改变
作用 横向伸缩
引起周期
问题3
作函数y=sin(x+ )和y=sin(x- )
的简图,并指出它们与y=sinx图象之
间的关系。
x
x+
sin(x+ )
0 1 0 -1 0
0 2
_
y=sinx
x
-1
1
o
y
-
y=sin(x+ )
兀
3
x
-1
1
o
y
-
x
x-
sin(x- )
0 1 0 -1 0
0 2
y=sinx
y=sin(x+ )
兀
3
y=sin(x- )
4
兀
小结3
(其中
)
函数
的图象
可以看作把正弦曲线上所有的点向左(当 >0时)或向右(当 <0时)平行移动| |个单位长度而得到.
作用 左右平移
向
左
( >0)
或
向
右
( <0)
平
移
| |
倍
A
的
来
原
为
变
标
坐
纵
横 坐 标 变 为 原 来 的 倍
问题4
?
并指出它们与y=sinx图象之间
的关系
y
3
2
-2
-3
x
1
o
-1
-
y=3sin(2x+ )
兀
3
五点法作图:
列表:
y
3
2
-2
-3
y=3sin(2x+ )
兀
3
y=sinx
y=sin(x+ )
兀
3
y=sin(2x+ )
兀
3
x
1
o
-1
-
注:先左右平移再横向伸缩
图象变换
1.
y
3
2
-2
-3
1
x
o
-1
-
y=sinx
y=sin2x
y=3sin(2x+ )
兀
3
注:先横向伸缩再左右平移
y =sin2(x+ )
兀
6
=sin(2x+ )
兀
3
图象变换
2.
y=sinx的图象上所有的点向左(当 >0时) 或向右(当 <0时)平行移动| |个度,得到y=sin(x+ );
把
所有点的横坐标缩短(当 >1时)或伸长(当0< <1时)到原来的 倍(纵坐标不变),得到y=sin( x+ );
再把
所有点的纵坐标伸长(当A>1时)或缩短(当0再把
函数y=Asin( x+ )(其中A>0, >0)的图象,可看作由下面方法得到:
变换1:
所有的点向左(当 >0时)或向右(当 <0时)平行移动| |个单位长度,得到y=sin(x+ ) =sin( x+ ); (注意)
再把
所有点的纵坐标伸长(当A>1时)或缩短(当0再把
y=sinx图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时)到原来的 倍(纵坐标不变),得到y=sin x;
把
函数y=Asin( x+ )(其中A>0, >0)的图象,可看作由下面方法得到:
变换2:
1、函数y=2sin(3x- )的图象是由y=sinx
的图象怎样变换得到的?
2、函数y=sin(2x- )的图象是由y=sin2x的
图象怎样平移得到的?
当堂练习:
请归纳这节课所学的内容
函数 的图像
1.5 三角函数图像平移伸缩变换
人教版高中数学必修四
y=sinx
最高点
曲线与x轴交点
-1
1
o
y
x
的图象的关键点是:(如图)
最低点
复习:
2.用五点法作函数
在同一坐标系中作出y=2sinx及 y= sinx的简图,并指出它们与y=sinx图象间的关系.
1
2
问题1
新课:
y=2sinx
y=sinx
y= sinx
1
2
x
2
-2
-1
1
o
y
0
0
0
0
0 1 0 -1 0
0 2 0 -2 0
可以看作把正弦曲线上所有点的纵坐标伸长(当A>1时)或缩短(当0
(其中
且
)
函数
的图象
函数
的值域是
A的作用 纵向伸缩
改变
引起值域
问题2
在同一坐标系中作出函数y=sin2x及y=sin x的简图,并指出它们y=sinx图象间的关系。
1
2
x
2x
sin2x
x
-1
1
o
y
0
0
y=sinx
y=sin2x
0 0 0
1
-1
x
-1
1
o
y
x
x
sin x
0 2
0
0 1 0 -1 0
1
2
y=sin x
1
2
y=sinx
y=sin2x
小结2
(其中
且
)
函数
的图象
可以看作把正弦曲线上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时)到原来的 倍(纵坐标不变)而得到.
T= 改变
作用 横向伸缩
引起周期
问题3
作函数y=sin(x+ )和y=sin(x- )
的简图,并指出它们与y=sinx图象之
间的关系。
x
x+
sin(x+ )
0 1 0 -1 0
0 2
_
y=sinx
x
-1
1
o
y
-
y=sin(x+ )
兀
3
x
-1
1
o
y
-
x
x-
sin(x- )
0 1 0 -1 0
0 2
y=sinx
y=sin(x+ )
兀
3
y=sin(x- )
4
兀
小结3
(其中
)
函数
的图象
可以看作把正弦曲线上所有的点向左(当 >0时)或向右(当 <0时)平行移动| |个单位长度而得到.
作用 左右平移
向
左
( >0)
或
向
右
( <0)
平
移
| |
倍
A
的
来
原
为
变
标
坐
纵
横 坐 标 变 为 原 来 的 倍
问题4
?
并指出它们与y=sinx图象之间
的关系
y
3
2
-2
-3
x
1
o
-1
-
y=3sin(2x+ )
兀
3
五点法作图:
列表:
y
3
2
-2
-3
y=3sin(2x+ )
兀
3
y=sinx
y=sin(x+ )
兀
3
y=sin(2x+ )
兀
3
x
1
o
-1
-
注:先左右平移再横向伸缩
图象变换
1.
y
3
2
-2
-3
1
x
o
-1
-
y=sinx
y=sin2x
y=3sin(2x+ )
兀
3
注:先横向伸缩再左右平移
y =sin2(x+ )
兀
6
=sin(2x+ )
兀
3
图象变换
2.
y=sinx的图象上所有的点向左(当 >0时) 或向右(当 <0时)平行移动| |个度,得到y=sin(x+ );
把
所有点的横坐标缩短(当 >1时)或伸长(当0< <1时)到原来的 倍(纵坐标不变),得到y=sin( x+ );
再把
所有点的纵坐标伸长(当A>1时)或缩短(当0
函数y=Asin( x+ )(其中A>0, >0)的图象,可看作由下面方法得到:
变换1:
所有的点向左(当 >0时)或向右(当 <0时)平行移动| |个单位长度,得到y=sin(x+ ) =sin( x+ ); (注意)
再把
所有点的纵坐标伸长(当A>1时)或缩短(当0
y=sinx图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时)到原来的 倍(纵坐标不变),得到y=sin x;
把
函数y=Asin( x+ )(其中A>0, >0)的图象,可看作由下面方法得到:
变换2:
1、函数y=2sin(3x- )的图象是由y=sinx
的图象怎样变换得到的?
2、函数y=sin(2x- )的图象是由y=sin2x的
图象怎样平移得到的?
当堂练习:
请归纳这节课所学的内容
