人教版九年级数学下册第二十九章《视图与投影》 检测题(含答案)
文档属性
| 名称 | 人教版九年级数学下册第二十九章《视图与投影》 检测题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 782.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览



文档简介
2020春季人教版九年级数学下第二十九章《视图与投影》检测题
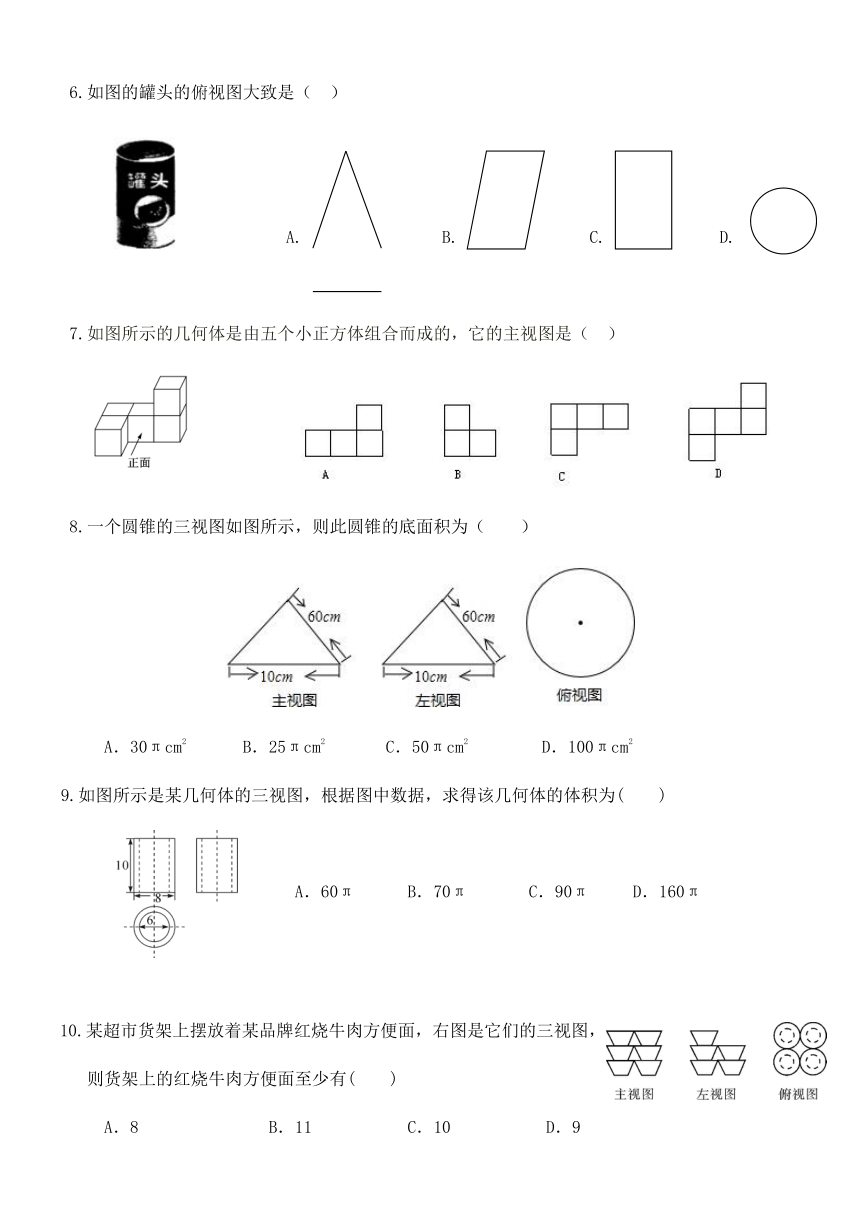
一、选择题(每题3分,共30分)
1.下列结论中正确的有( )
①同一地点、同一时刻,不同物体在阳光照射下,影子的方向是相同的;
②不同物体在任何光线照射下影子的方向都是相同的;
③同一物体在路灯照射下,影子的方向与路灯的位置有关;
④物体在光线照射下,影子的长短仅与物体的长短有关.
A.1个 B.2个 C.3个 D.4个
2.如图是由两个相同的小正方体和一个圆锥体组成的立体图形,其俯视图是( )
3.王丽同学在某天下午的不同时刻拍了三张同一景物的风景照A,B,C,冲洗后不知道拍照的顺序,已知投影lA>lC>lB,则A,B,C的先后顺序是( )
A.A,B,C B.A,C,B C.B,C,A D.B,A,C
4.由一些完全相同的小正方体搭成的几何体的主视图、
俯视图如图所示,那么搭成这个几何体至少需用小
正方体的个数是( )
A.8个 B.7个 C.6个 D.5个
5.一个正方体被截去四个角后得到一个几何体(如图),它的俯视图是( )
6.如图的罐头的俯视图大致是( )
A. B. C. D.
7.如图所示的几何体是由五个小正方体组合而成的,它的主视图是( )
8.一个圆锥的三视图如图所示,则此圆锥的底面积为( )
A.30πcm2 B.25πcm2 C.50πcm2 D.100πcm2
9.如图所示是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A.60π B.70π C.90π D.160π
10.某超市货架上摆放着某品牌红烧牛肉方便面,右图是它们的三视图,
则货架上的红烧牛肉方便面至少有( )
A.8 B.11 C.10 D.9
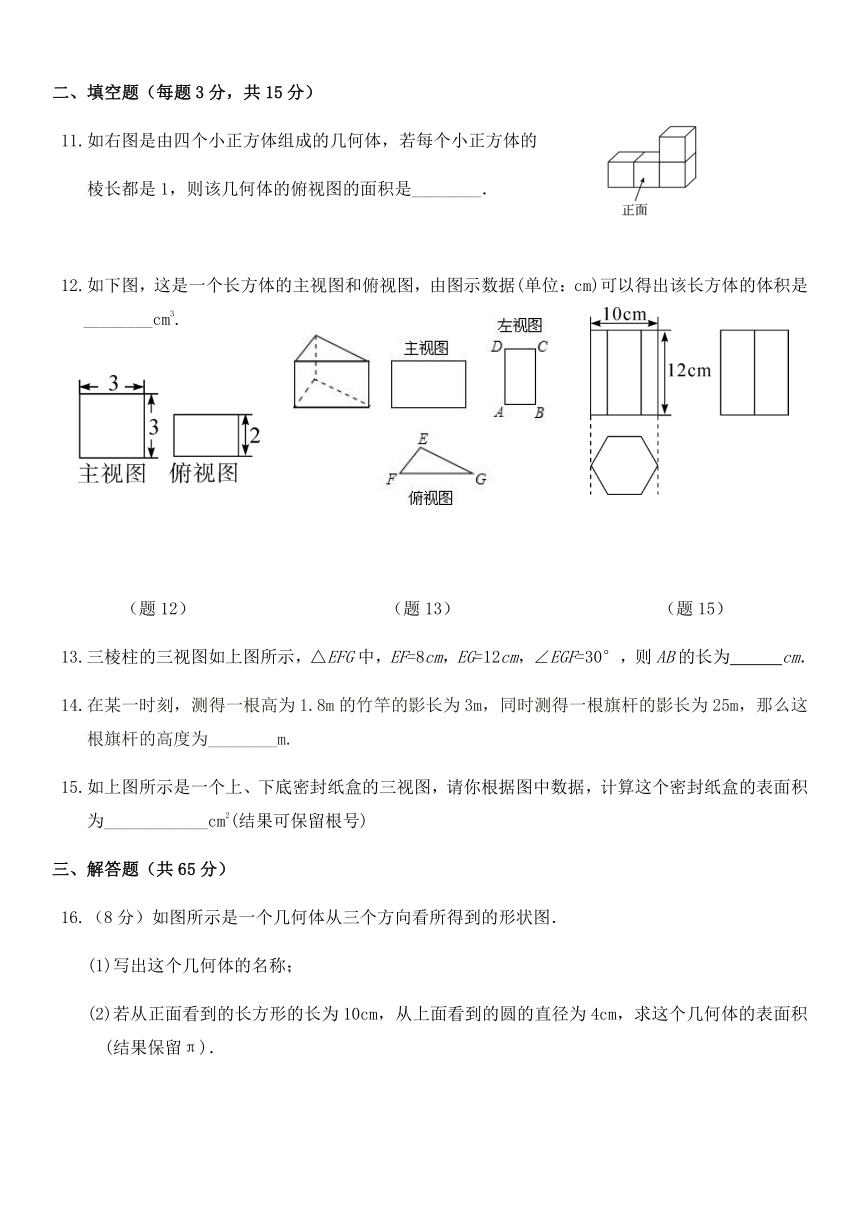
二、填空题(每题3分,共15分)
11.如右图是由四个小正方体组成的几何体,若每个小正方体的
棱长都是1,则该几何体的俯视图的面积是________.
12.如下图,这是一个长方体的主视图和俯视图,由图示数据(单位:cm)可以得出该长方体的体积是________cm3.
(题12) (题13) (题15)
13.三棱柱的三视图如上图所示,△EFG中,EF=8cm,EG=12cm,∠EGF=30°,则AB的长为 cm.
14.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为________m.
15.如上图所示是一个上、下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为____________cm2(结果可保留根号)
三、解答题(共65分)
16.(8分)如图所示是一个几何体从三个方向看所得到的形状图.
(1)写出这个几何体的名称;
(2)若从正面看到的长方形的长为10cm,从上面看到的圆的直径为4cm,求这个几何体的表面积(结果保留π).
17.(9分)如图所示是由一些大小相同的小正方体组成的几何体的主视图和俯视图.
(1)当组成这个几何体的小正方体的个数为8个时,几何体有多种形状.
请画出其中两种几何体的左视图;
(2)若组成这个几何体的小正方体的个数为n,请写出n的最小值和最大值;
(3)主视图和俯视图为下面两图的几何体有若干个,请你画出其中一个几何体.
18.(9分)如图,已知线段AB=2 cm,投影面为P,太阳光线与投影面垂直.
(1)当AB垂直于投影面P时(如图①),请画出线段AB的投影;
(2)当AB平行于投影面P时(如图②),请画出它的投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图③中画出线段AB的正投影,并求出其正投影的长.
19.(9分)如图,有一辆客车在平坦的大路上行驶,前方有两座建筑物,且A,B两处的建筑物的高度分别为12 m和24 m,当汽车行驶到C处,CF=30 m时,求司机可以看到的B处楼房的高度?
20.(9分)如图 (单位:cm)是某校升旗台的三视图.
(1)画出台阶的立体模型;
(2)计算出台阶的体积.
21.(10分)如图,小华在晚上由路灯AC走向路灯BD.当他走到点P时,发现他身后影子的顶部刚好接触到路灯AC的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯BD的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离;
(2)当小华走到路灯BD的底部时,他在路灯AC下的影长是多少?
22.(10分)如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一段高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米.依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是投影的有关知识进行计算的.
(2)试计算出电线杆的高度,并写出计算的过程
23.(11分)某中学广场上有旗杆如图①所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图②,AB⊥BC,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米.参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08).
参考答案
1-10 BCCAC DABBD
11.3 12.18 13. 6 14.15 15. (75+360)
16. 解:(1)该几何体是圆柱.(3分)
(2)由题意得该圆柱的底面直径为4cm,高为10cm,(4分)
∴该几何体的侧面积为2π××10=40π(cm2),(6分)
底面积为π·=4π(cm2).
∴该几何体的表面积为40π+2×4π=48π(cm2).(8分)
17. 解:(1)如图所示.(2分)
(2)这个几何体的小正方体的个数最少为8个,最多为11个.即n最小为8,最大为11.(5分)
(3)如图所示(答案不唯一).(9分)
18. 解:(1)如图①,点C即为所求.
(2)如图②,线段CD即为所求,正投影的长为2 cm.
(3)如图③,线段CD即为所求,正投影的长为2cos30°= cm.
19. 解:∵△CEF∽△CDG,∴=,
DG===18(m).
∴C处汽车司机可看到的B处楼房的高度为
24-18=6 (m).
答:C处汽车司机可看到的B处楼房的高度为6 m.
20. 解:(1)立体模型如图D108(单位:cm).
图D108
(2)台阶的体积可以用三个长方体的体积来求得
V=V1+V2+V3=150×(800+1600+2400)=150×4800=720 000(cm3).
21. 解:(1)∵PM∥BD,
∴△APM∽△ABD,
∴=,即=,
∴AP=AB.(3分)
∵AP=QB,
∴QB=AB.(4分)
∵AP+PQ+QB=AB,
∴AB+12+AB=AB,
∴AB=18m.(6分)
答:两个路灯之间的距离为18m.(7分)
(2)如图,小华在路灯AC下的影子为BF.
∵BE∥AC,
∴△FBE∽△FAC,(9分)
∴=,即=,
∴BF=3.6m.
答:当小华走到路灯BD的底部时,他在路灯AC下的影长是3.6m.(10分)
22. 分析:(1)这个投影的光线是太阳光,太阳光可以看成是平行光线,所以这个投影是平行投影.(2)根据平行投影中物高与影长成比例,列出比例式,由比例的性质求解.
解:(1)平行.
(2)如图,过点E作EM⊥AB于M,过点G作GN⊥CD于N,
则MB=EF=2,ND=GH=3,
ME=BF=10,NG=DH=5.所以AM=10-2=8.
由平行投影可知,即=,
解得CD=7,即电线杆的高度为7米.
23. 解:作CM∥AB交AD于M,作MN⊥AB于N,
则MN=BC=4米,BN=CM.(3分)
由题意得=,即=,
∴CM=米,∴BN=米.(6分)
在Rt△AMN中,∵∠ANM=90°,MN=4米,∠AMN=72°,
∴tan72°=,∴AN≈12.3米.(9分)
∴AB=AN+BN≈12.3+=13.8(米).(10分)
答:旗杆的高度约为13.8米.(11分)
