人教版选修2-2第二章推理与证明2.3《数学归纳法》(共26页ppt)
文档属性
| 名称 | 人教版选修2-2第二章推理与证明2.3《数学归纳法》(共26页ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览

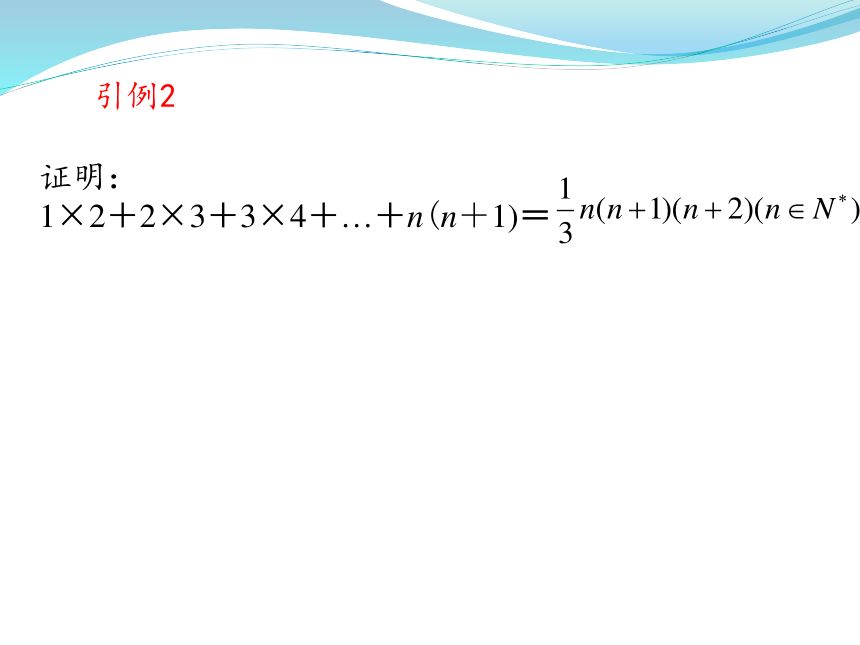



文档简介
(共26张PPT)
完全归纳法
*
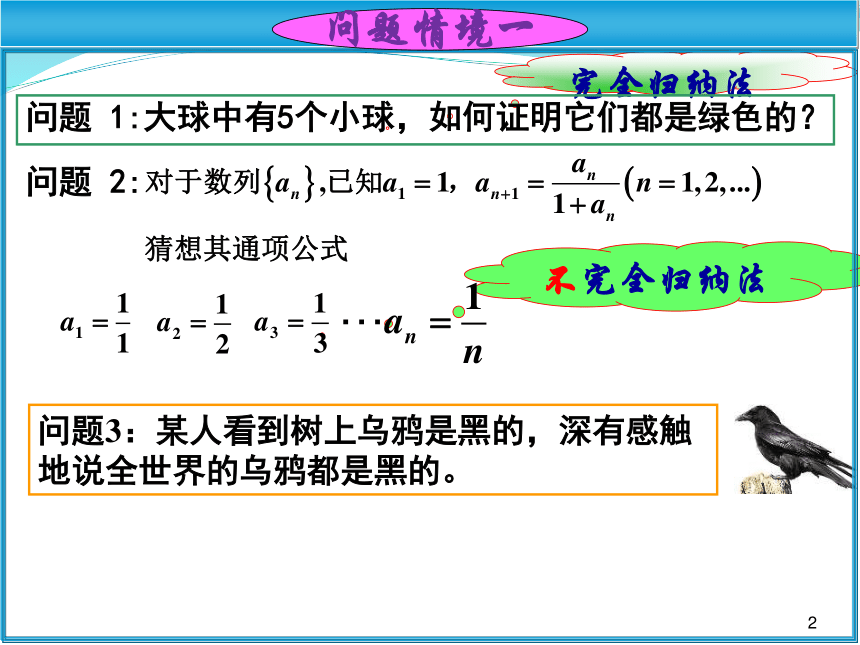
问题 1:大球中有5个小球,如何证明它们都是绿色的?
问题 2:
不完全归纳法
…
问题情境一
*
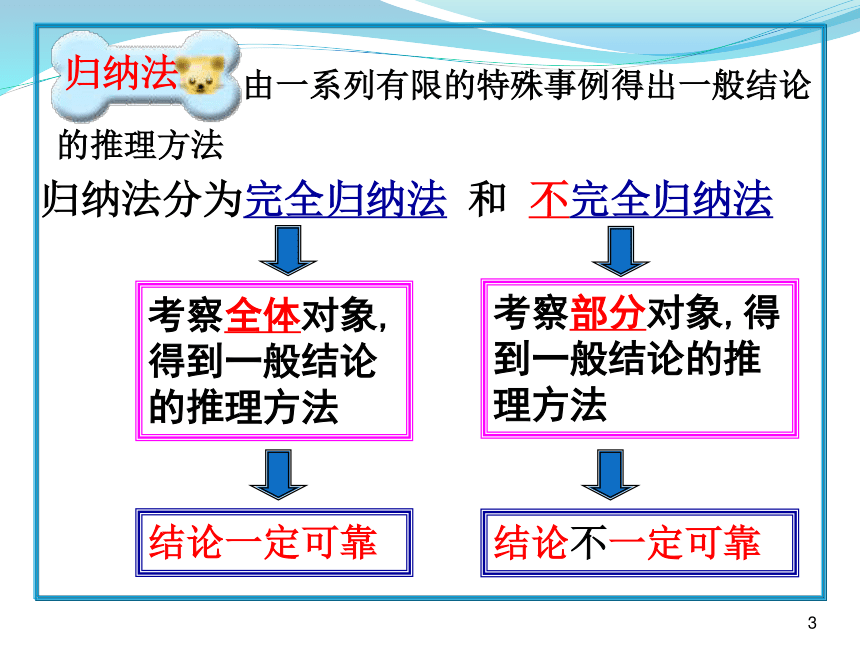
:由一系列有限的特殊事例得出一般结论的推理方法
结论一定可靠
结论不一定可靠
考察全体对象,得到一般结论的推理方法
考察部分对象,得到一般结论的推理方法
归纳法分为完全归纳法 和 不完全归纳法
引例2
证明:
1×2+2×3+3×4+…+n(n+1)=
简化的多米诺骨牌游戏
*
(2)验证前一问题与后一问题有递推关系;
(相当于前牌推倒后牌)
(1)处理第一个问题;(相当于推倒第一块骨牌)
问题情境三
*
由条件知,n=1时猜想成立.
即n=k+1时猜想也成立.
*
对于由不完全归纳法得到的某些与自然数有关自然数的数学命题我们常采用下面的方法来证明它们的正确性:
(1)证明当n取第一个值n0(例如n0=1) 时命题成立;
(2)假设当n=k(k∈N* ,k≥ n0)时命题成立
证明当n=k+1时命题也成立.
这种证明方法叫做 数学归纳法
【归纳递推】
【归纳奠基】
数学归纳法
*
框图表示
数学归纳法
三、数学归纳法书写格式
证明某些与正整数n有关的命题.
先验证当n取第一个值n0时,命题成立;
2.然后假设当n=k(k?N*,k≥n0) 命题成立的前提下 ,证明(?)当n=k+1时,命题也成立.
由1、2可以推断命题从n0开始的?n?N*,命题都成立.
命题成立
命题也成立
命题都成立
注:书写格式--2个步骤,3个结论.
1. 验证
当n=k(k?N*,k≥n0) 命题成立
当n=k的归纳条件一定要用.证明传递性、延续性.
2.
(注1)验证:n取第一个值n0时,左边= 右边=
(注2)证明当n=k+1命题成立时,必须要用到假设!
从n=k到n=k+1有什么变化
证明:
则当n=k+1时,
变式练1 用数学归纳法证明:
变式练2 用数学归纳法证明:
1+3+5+‥+(2n-1)=n2
变式练1 用数学归纳法证明:
即当n=k+1时等式也成立.
证明:
1+3+5+‥+(2k-1)+[2(k+1)-1]
那么当n=k+1时
(2)假设当n=k时,等式成立,即
(1)当n=1时,左边=1,右边=1,等式成立。
变式练2 用数学归纳法证明:
则当 时,
根据(1)和(2)可知,等式对任何 都成立。
即当n=k+1时等式也成立.
例2 用数学归纳法证明等式 1+2+3+…+(2n+1)=(n+1)(2n+1)(n?N*)时,
当n=1时,左边所得项是 ;
当n=2时,左边所得项是 ;
1+2+3
1+2+3+4+5
证明:(1)当n=1时,左=1+2+3=6,右=(1+1)×(2×1+1)=6
(2)假设当n=k(k∈N*,k≥1)等式成立,即
即当n=k+1时等式也成立.
1+2+3+···+(2k+1)+
那么当n=k+1时
= (k+1)(2k+1)+(2k+2)+(2k+3)
= (k+1)(2k+1+2)+(2k+3) =(k+2)(2k+3)
(2k+2)+(2k+3)
深化巩固
A
变式练4
例3
学习小结
附数学归纳法打油诗一首:
两个步骤一结论,递推基础不可少,
归纳假设要用到,结论写明莫忘掉。
数学归纳法是一种证明与自然数有关的数学命题的重要方法。其格式主要有两个步骤、一个结论:
(1)证明当n取第一个值n0时结论正确;
验证初始条件
(2)假设n=k时结论正确,在假设之下,证明n=k+1时结论也正确;
假设推理
(3)由(1)、(2)得出结论.
下结论
找准起点,奠基要稳
用上假设
递推才真
写明结论
才算完整
练习1
课堂练习
练习2
完全归纳法
*
问题 1:大球中有5个小球,如何证明它们都是绿色的?
问题 2:
不完全归纳法
…
问题情境一
*
:由一系列有限的特殊事例得出一般结论的推理方法
结论一定可靠
结论不一定可靠
考察全体对象,得到一般结论的推理方法
考察部分对象,得到一般结论的推理方法
归纳法分为完全归纳法 和 不完全归纳法
引例2
证明:
1×2+2×3+3×4+…+n(n+1)=
简化的多米诺骨牌游戏
*
(2)验证前一问题与后一问题有递推关系;
(相当于前牌推倒后牌)
(1)处理第一个问题;(相当于推倒第一块骨牌)
问题情境三
*
由条件知,n=1时猜想成立.
即n=k+1时猜想也成立.
*
对于由不完全归纳法得到的某些与自然数有关自然数的数学命题我们常采用下面的方法来证明它们的正确性:
(1)证明当n取第一个值n0(例如n0=1) 时命题成立;
(2)假设当n=k(k∈N* ,k≥ n0)时命题成立
证明当n=k+1时命题也成立.
这种证明方法叫做 数学归纳法
【归纳递推】
【归纳奠基】
数学归纳法
*
框图表示
数学归纳法
三、数学归纳法书写格式
证明某些与正整数n有关的命题.
先验证当n取第一个值n0时,命题成立;
2.然后假设当n=k(k?N*,k≥n0) 命题成立的前提下 ,证明(?)当n=k+1时,命题也成立.
由1、2可以推断命题从n0开始的?n?N*,命题都成立.
命题成立
命题也成立
命题都成立
注:书写格式--2个步骤,3个结论.
1. 验证
当n=k(k?N*,k≥n0) 命题成立
当n=k的归纳条件一定要用.证明传递性、延续性.
2.
(注1)验证:n取第一个值n0时,左边= 右边=
(注2)证明当n=k+1命题成立时,必须要用到假设!
从n=k到n=k+1有什么变化
证明:
则当n=k+1时,
变式练1 用数学归纳法证明:
变式练2 用数学归纳法证明:
1+3+5+‥+(2n-1)=n2
变式练1 用数学归纳法证明:
即当n=k+1时等式也成立.
证明:
1+3+5+‥+(2k-1)+[2(k+1)-1]
那么当n=k+1时
(2)假设当n=k时,等式成立,即
(1)当n=1时,左边=1,右边=1,等式成立。
变式练2 用数学归纳法证明:
则当 时,
根据(1)和(2)可知,等式对任何 都成立。
即当n=k+1时等式也成立.
例2 用数学归纳法证明等式 1+2+3+…+(2n+1)=(n+1)(2n+1)(n?N*)时,
当n=1时,左边所得项是 ;
当n=2时,左边所得项是 ;
1+2+3
1+2+3+4+5
证明:(1)当n=1时,左=1+2+3=6,右=(1+1)×(2×1+1)=6
(2)假设当n=k(k∈N*,k≥1)等式成立,即
即当n=k+1时等式也成立.
1+2+3+···+(2k+1)+
那么当n=k+1时
= (k+1)(2k+1)+(2k+2)+(2k+3)
= (k+1)(2k+1+2)+(2k+3) =(k+2)(2k+3)
(2k+2)+(2k+3)
深化巩固
A
变式练4
例3
学习小结
附数学归纳法打油诗一首:
两个步骤一结论,递推基础不可少,
归纳假设要用到,结论写明莫忘掉。
数学归纳法是一种证明与自然数有关的数学命题的重要方法。其格式主要有两个步骤、一个结论:
(1)证明当n取第一个值n0时结论正确;
验证初始条件
(2)假设n=k时结论正确,在假设之下,证明n=k+1时结论也正确;
假设推理
(3)由(1)、(2)得出结论.
下结论
找准起点,奠基要稳
用上假设
递推才真
写明结论
才算完整
练习1
课堂练习
练习2
