华师大版八年级数学下册19.1.2矩形的判定 课件(19张)
文档属性
| 名称 | 华师大版八年级数学下册19.1.2矩形的判定 课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 160.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
19.1.2 矩形的判定
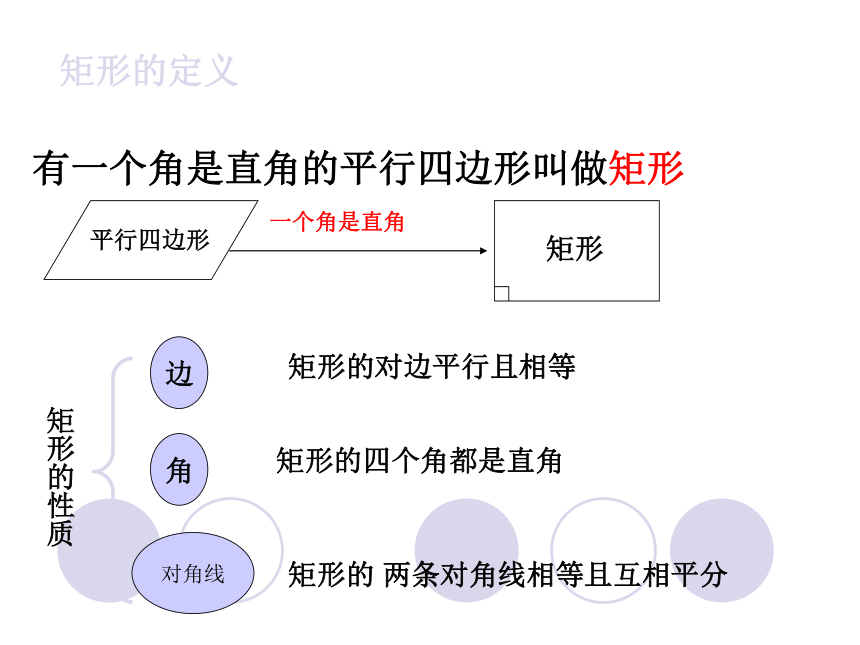
矩形的定义
有一个角是直角的平行四边形叫做矩形
一个角是直角
平行四边形
矩形
矩形的性质
边
角
对角线
矩形的对边平行且相等
矩形的四个角都是直角
矩形的 两条对角线相等且互相平分
思考与探究
一天,小丽和小美准备给肖华买生日礼物,选了半天,她们俩最后决定买相框送给她, 为了保证相框摆放的美观性,她们选择了矩形的相框,那么她们用什么方法可以知道她们拿的就是矩形相框呢?
请你思考:
她们需要度量什么能知道做好的相框是矩形呢?
能证明它的正确性吗?
度量两条对角线是否相等。
活动一:
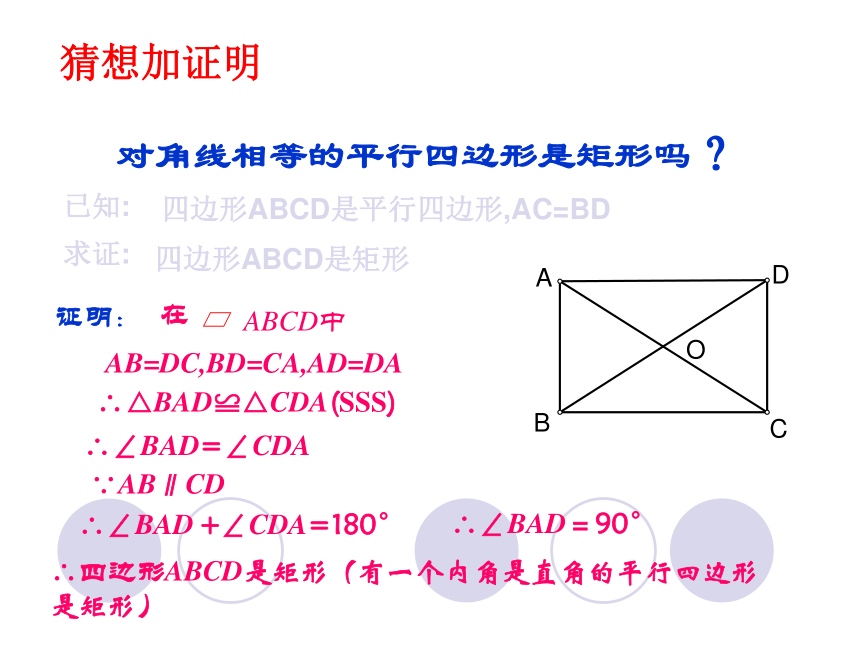
猜想加证明
对角线相等的平行四边形是矩形吗?
已知:
四边形ABCD是平行四边形,AC=BD
求证:
四边形ABCD是矩形
证明:
在
ABCD中
AB=DC,BD=CA,AD=DA
∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA
∵AB∥CD
∴∠BAD +∠CDA=180°
∴∠BAD=90°
∴四边形ABCD是矩形(有一个内角是直角的平行四边形是矩形)
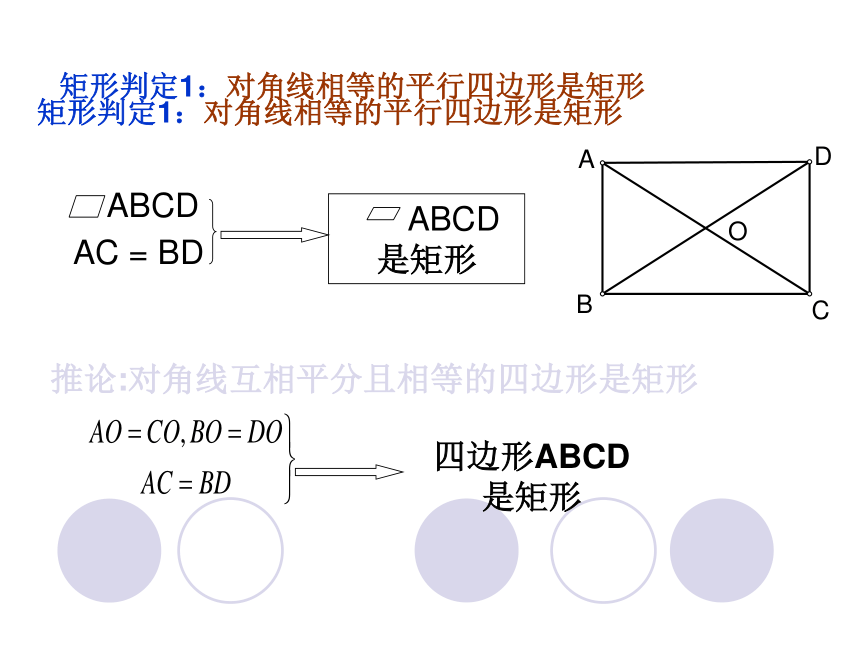
矩形判定1:对角线相等的平行四边形是矩形
矩形判定1:对角线相等的平行四边形是矩形
ABCD
AC = BD
ABCD
是矩形
推论:对角线互相平分且相等的四边形是矩形
四边形ABCD
是矩形
实际应用
这一判定方法在生活中有许多用处,木工师傅在制作门框或其他矩形的物体时,常用策略对角线的方法,来检验产品师傅符合要求。
小丽和吴娟是怎样知道所买的相框是矩形的呢?
还有没有其它的方法?能不能从角上考虑?
通过测量四个角是直角
请你思考
猜想加证明
有三个角是直角的四边形是矩形吗?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:
∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
D
B
C
A
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
矩形判定2:有三个角是直角的四边形是矩形
∠A= ∠B= ∠C=90°
四边形ABCD
是矩形
D
B
C
A
活动二:
1、为了庆祝十一国庆节,八年级(3)班同学要在广场上布置一个矩形的花坛。计划用“串红”摆成两条对角线。如果一条对角线用了37盆“串红”,还 需要从花房运来多少盆“串红”?为什么?如果一条对角线用了48盆呢?为什么?
课堂练习:
一.选择题
(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等(C)对边平行且相等(D)对角线相等
(2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等(C)是轴对称图形(D)对角线垂直
二.判断题
(1)对角线相等的四边形是矩形。
(2)对角线互相平分且相等的四边形是矩形。
(3)有一个角是直角的四边形是矩形。
(4)四个角都是直角的四边形是矩形。
(5)四个角都相等的四边形是矩形。
(6)对角线相等且有一个角是直角的四边形是矩形。
(7)对角线相等且互相垂直的四边形是矩形。
其中(2)、(4)、(5)对
二.判断题
(1)对角线相等的四边形是矩形。
(2)对角线互相平分且相等的四边形是矩形。
(3)有一个角是直角的四边形是矩形。
(4)四个角都是直角的四边形是矩形。
(5)四个角都相等的四边形是矩形。
(6)对角线相等且有一个角是直角的四边形是矩形。
(7)对角线相等且互相垂直的四边形是矩形。
例 1 已知:如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,求证四边形EFGH是矩形.
证明:
∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等)
AO=BO=CO=DO(矩形的对角线互相平分)
∵ E、F、G、H分别是AO、BO、
CO、DO的中点
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形(对角
线互相平分的四边形是平行四边形)
∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形(对角线相等的
平行四边形是矩形)。
变式一:
已知:如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G 、 H分别是AO 、BO 、 CO 、 DO上的一点 ,且AE=BF=CG=DH.
B
C
D
E
F
G
H
O
A
求证:四边形EFGH是矩形
课堂小结
这节课你有什么收获?
ABCD
AC = BD
ABCD
是矩形
∠A= ∠B= ∠C=90°
四边形ABCD
是矩形
再见
19.1.2 矩形的判定
矩形的定义
有一个角是直角的平行四边形叫做矩形
一个角是直角
平行四边形
矩形
矩形的性质
边
角
对角线
矩形的对边平行且相等
矩形的四个角都是直角
矩形的 两条对角线相等且互相平分
思考与探究
一天,小丽和小美准备给肖华买生日礼物,选了半天,她们俩最后决定买相框送给她, 为了保证相框摆放的美观性,她们选择了矩形的相框,那么她们用什么方法可以知道她们拿的就是矩形相框呢?
请你思考:
她们需要度量什么能知道做好的相框是矩形呢?
能证明它的正确性吗?
度量两条对角线是否相等。
活动一:
猜想加证明
对角线相等的平行四边形是矩形吗?
已知:
四边形ABCD是平行四边形,AC=BD
求证:
四边形ABCD是矩形
证明:
在
ABCD中
AB=DC,BD=CA,AD=DA
∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA
∵AB∥CD
∴∠BAD +∠CDA=180°
∴∠BAD=90°
∴四边形ABCD是矩形(有一个内角是直角的平行四边形是矩形)
矩形判定1:对角线相等的平行四边形是矩形
矩形判定1:对角线相等的平行四边形是矩形
ABCD
AC = BD
ABCD
是矩形
推论:对角线互相平分且相等的四边形是矩形
四边形ABCD
是矩形
实际应用
这一判定方法在生活中有许多用处,木工师傅在制作门框或其他矩形的物体时,常用策略对角线的方法,来检验产品师傅符合要求。
小丽和吴娟是怎样知道所买的相框是矩形的呢?
还有没有其它的方法?能不能从角上考虑?
通过测量四个角是直角
请你思考
猜想加证明
有三个角是直角的四边形是矩形吗?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:
∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
D
B
C
A
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
矩形判定2:有三个角是直角的四边形是矩形
∠A= ∠B= ∠C=90°
四边形ABCD
是矩形
D
B
C
A
活动二:
1、为了庆祝十一国庆节,八年级(3)班同学要在广场上布置一个矩形的花坛。计划用“串红”摆成两条对角线。如果一条对角线用了37盆“串红”,还 需要从花房运来多少盆“串红”?为什么?如果一条对角线用了48盆呢?为什么?
课堂练习:
一.选择题
(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等(C)对边平行且相等(D)对角线相等
(2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等(C)是轴对称图形(D)对角线垂直
二.判断题
(1)对角线相等的四边形是矩形。
(2)对角线互相平分且相等的四边形是矩形。
(3)有一个角是直角的四边形是矩形。
(4)四个角都是直角的四边形是矩形。
(5)四个角都相等的四边形是矩形。
(6)对角线相等且有一个角是直角的四边形是矩形。
(7)对角线相等且互相垂直的四边形是矩形。
其中(2)、(4)、(5)对
二.判断题
(1)对角线相等的四边形是矩形。
(2)对角线互相平分且相等的四边形是矩形。
(3)有一个角是直角的四边形是矩形。
(4)四个角都是直角的四边形是矩形。
(5)四个角都相等的四边形是矩形。
(6)对角线相等且有一个角是直角的四边形是矩形。
(7)对角线相等且互相垂直的四边形是矩形。
例 1 已知:如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,求证四边形EFGH是矩形.
证明:
∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等)
AO=BO=CO=DO(矩形的对角线互相平分)
∵ E、F、G、H分别是AO、BO、
CO、DO的中点
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形(对角
线互相平分的四边形是平行四边形)
∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形(对角线相等的
平行四边形是矩形)。
变式一:
已知:如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G 、 H分别是AO 、BO 、 CO 、 DO上的一点 ,且AE=BF=CG=DH.
B
C
D
E
F
G
H
O
A
求证:四边形EFGH是矩形
课堂小结
这节课你有什么收获?
ABCD
AC = BD
ABCD
是矩形
∠A= ∠B= ∠C=90°
四边形ABCD
是矩形
再见
