人教版九年级数学上册24.1.3弧、弦、圆心角课件(24张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.1.3弧、弦、圆心角课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 414.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-17 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
24.1.3
弧、弦、圆心角
学习目标:(1分钟)
1.理解圆心角、弧、弦、(弦心距)之间的概念;
2.理解圆的对称性及相关性质。
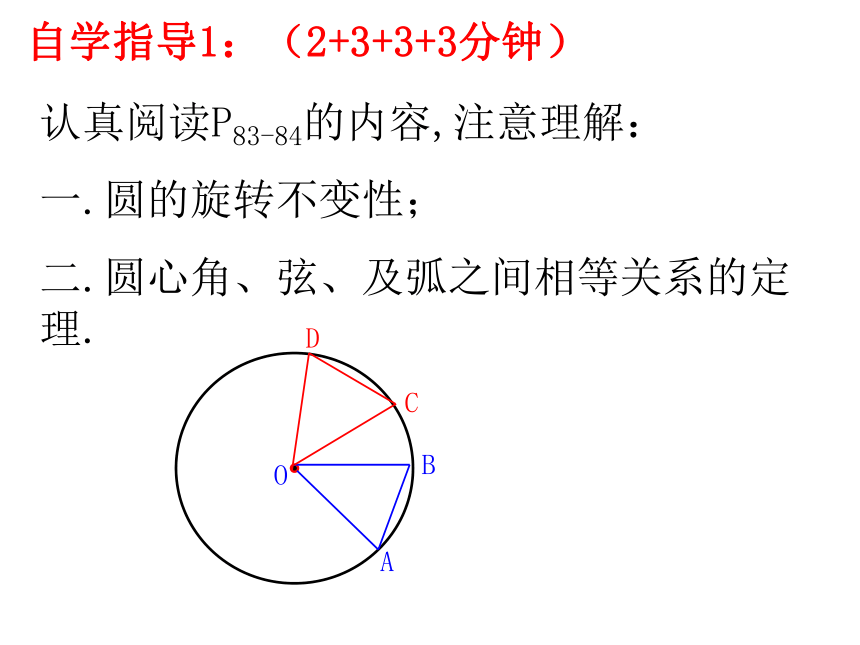
自学指导1:(2+3+3+3分钟)
认真阅读P83-84的内容,注意理解:
一.圆的旋转不变性;
二.圆心角、弦、及弧之间相等关系的定理.
1.圆的旋转不变性圆是_________图形,而且圆绕圆心旋转任意一个角度都能与原图形_____.
2.圆心角___________的角叫做圆心角.
3.圆心角、弦、弧的关系
①在同圆或等圆中,相等的圆心角所对的___相等,所对的___也相等;
②在同圆或等圆中,如果两条弧相等,那么它们所对的_______相等,
所对的___相等;
③在同圆或等圆中,如果两条弦相等,那么它们所对的_______相等,
所对的___也相等;
【结论】在同圆或等圆中,___________、_______、_______中如果
有___组量相等,则它们所对应的其余各组量也相等.
中心对称
重合
顶点在圆心
弧
弦
圆心角
弦
圆心角
弧
两个圆心角
两条弧
两条弦
一
结合图形,用几何语言表述3:
①
②
③
38妇女节讲话稿:无影灯下天使情
38妇女节演讲稿:无影灯下天使情
各位领导、各位评委,来宾们,同事们:大家好!
很荣幸我能有这样的机会参加今天的演讲,我是手术室的一名普通护士。我演讲的题目是:无影灯下天使情。
记得我刚踏上手术室岗位的时候,心里充满了对新生活的美好憧憬,无影灯下,我曾用自己火样的热情和赤诚去描绘着自己未来的事业。然而,现实并不像伊甸园的菩提果那般完美和甜蜜。我每天要面对着的是一张张被病痛扭曲的面孔,听到的是一声声长吁短叹,一阵阵抽泣呜咽……永远忙碌的脚步分不清时间的分分秒秒,#个小时,#个小时,甚至##几个小时,腿酸了要站得住,肚子饿了要挺得住,眼睛困了要熬得住……多少个深夜,我们被急诊电话惊醒,不管是雷电交加或是风啸雪寒,也得从温暖的被窝爬起来,冲入沉沉的黑夜之。紧张、劳累的工作,我真正体验到了手术室护士平凡生活的滋味,体验到了其的艰辛和压力。我苦恼过、迷惘过;苦恼迷惘之后也曾动摇过、退却过。但有一件事深深地触动了我,使我从迷惘寻回了自我,在退却时坚定了初衷。
《比赛评分系统》是按照时下流行的评委打分方式设计,有比较完善的竞赛评分功能。运用互动式多媒体技术。通过投影
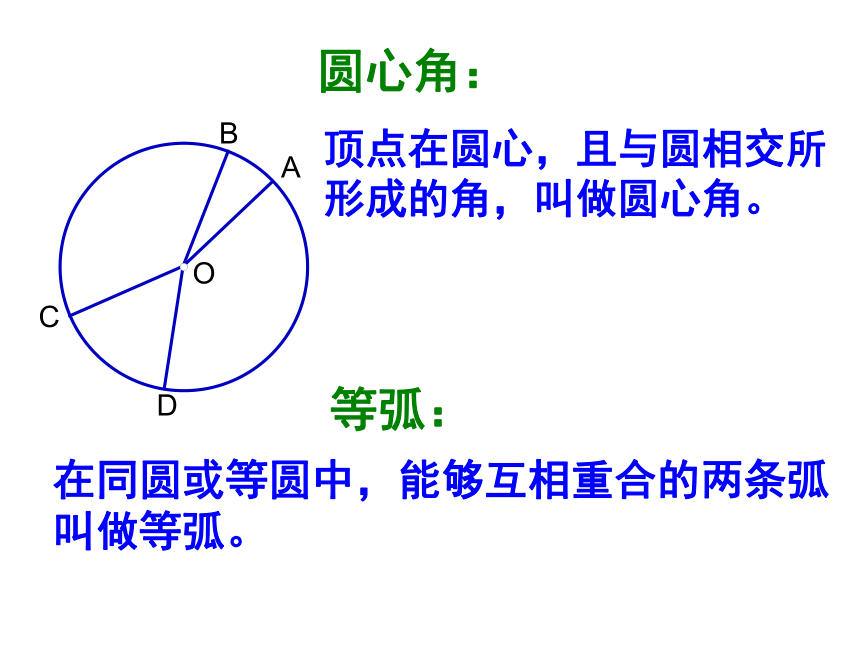
圆心角:
等弧:
在同圆或等圆中,能够互相重合的两条弧叫做等弧。
顶点在圆心,且与圆相交所形成的角,叫做圆心角。
弦心距:
O
C
A
B
M
圆心角:顶点在圆心的角,叫圆心角,如∠AOB .
圆心角 ∠AOB所对的弦为AB.
任意给圆心角,对应出现三个量:
圆心角
弧
弦
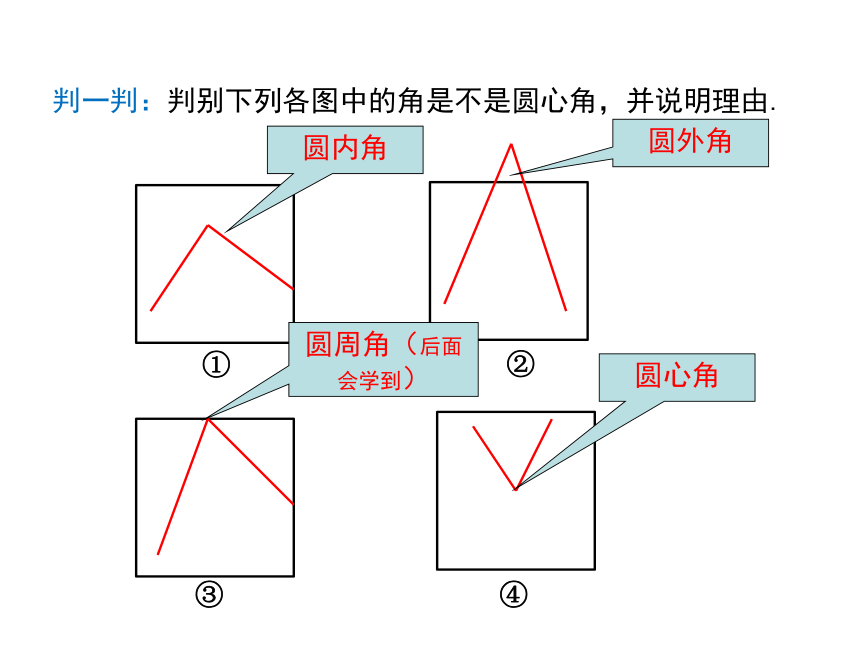
判一判:判别下列各图中的角是不是圆心角,并说明理由.
①
②
③
④
圆内角
圆外角
圆周角(后面会学到)
圆心角
圆心角、弧、弦、弦心距之间的关系
在等圆中
1.这两个相等的圆心角所对的弦分别是哪两条?
它们相等吗?
2.这两个相等的圆心角所对的弧分别是哪两条?
它们相等吗?
如果两个圆心角相等
叠合法
圆心角、弧、弦、弦心距之间的关系
在同圆或等圆中,
相等的圆心角所对的弧相等,
所对的弦相等。
前提条件
AB=CD ?
在同圆或等圆中,
相等的圆心角所对的弧相等,
所对的弦相等。
想一想:定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
思考:在同圆内作两条长度相同的弦,它们所对的圆心角相等吗?所对的弧相等吗?
圆心角、弧、弦、弦心距之间的关系
在同圆或等圆中,
如果两个圆心角、
两条弧、
两条弦
中有一组量相等,那么它们所对应的其余各组量都分别相等。
简称“知一推二”
或“知一推三”
三、仔细阅读课本84页例题3. 注意解题格式!
仿照例题完成课本85页练习.
(4)解:OE=OF. 理由如下,
1.判断对错:
(1)圆心角的顶点在圆心上. ( )
(2)相等的圆心角所对的弧一定相等.( )
(3)等弧所对的圆心角一定相等. ( )
(4)相等的弦所对的弧相等.( )
2.长度等于半径的弦所对的圆心角的度数为( )
A.60° B.45° C.90° D.120°
3.点A,B,C三点在☉O上,且AB=BC=AC,那么
∠AOB= ______.
4.如图,若 长为☉O周长的 ,则∠AOB=________.
5.如图,A,B是☉O上的两点,∠AOB=120°,
C是 的中点,判断四边形OACB的形状
并证明你的结论.
√
×
√
×
A
自学检测(10分钟)
120°
解:四边形OACB是菱形.理由如下:
∵C是 的中点,
∴ ∴∠AOC=∠BOC,
又∵∠AOB=120°,∴∠AOC=∠BOC=60°,
∵OA=OC,∴△AOC是等边三角形.
∴OA=OC=AC.同理可证OB=OC=BC,
∴OA=AC=CB=OB,
∴四边形OACB是菱形.
【规律总结】同一圆中证明两弦相等的“四种方法”:
1.若两弦位于两个不同的三角形,证明两弦所在的三角形全等.
2.若两弦位于同一个三角形中,根据等角对等边证明两弦相等.
3.证明两弦所对的弧相等.
4.证明两弦所对的圆心角相等.
证两条线段相等.
6.如图,以 ABCD的顶点A为圆心,AB为半径作☉A,分别交AD,BC于E,F,延长BA交☉A于G,求证:
7. 如图,在☉O中,C,D是直径AB上两点,AC=BD,MC⊥AB,
ND⊥AB,M,N在☉O上.求证:
9.如图, ⊙O中弦AB⊥AC,D,E分别是AB,AC的中点.若AB=AC,
则四边形OEAD是 形;
8.如图:已知AB、CD是⊙O两条直径,弦CE∥AB,弧EC的度数为40°,则∠BOC=______.
A
B
C
D
E
O
1100
正方形
弧的度数等于它所对的圆心角的度数.
11.如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ,则a的值是 .
A
B
O
P
x
y
y=x
E
F
H
12.如图,在⊙O中,弦AB与CD相交于点E,AB=CD.
(1)求证:△AEC≌△DEB;
(2)点B与点C关于直线OE对称吗?试说明理由.
A
B
C
D
O
E
小结(1分钟)
1.圆的对称性:
2.圆心角、弦、及弧之间相等关系的定理:
圆是轴对称图形,对称轴是任意一条过圆心的直线 ;圆是中心对称图形,对称中心为圆心.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
两条弦心距
两条弦心距
24.1.3
弧、弦、圆心角
学习目标:(1分钟)
1.理解圆心角、弧、弦、(弦心距)之间的概念;
2.理解圆的对称性及相关性质。
自学指导1:(2+3+3+3分钟)
认真阅读P83-84的内容,注意理解:
一.圆的旋转不变性;
二.圆心角、弦、及弧之间相等关系的定理.
1.圆的旋转不变性圆是_________图形,而且圆绕圆心旋转任意一个角度都能与原图形_____.
2.圆心角___________的角叫做圆心角.
3.圆心角、弦、弧的关系
①在同圆或等圆中,相等的圆心角所对的___相等,所对的___也相等;
②在同圆或等圆中,如果两条弧相等,那么它们所对的_______相等,
所对的___相等;
③在同圆或等圆中,如果两条弦相等,那么它们所对的_______相等,
所对的___也相等;
【结论】在同圆或等圆中,___________、_______、_______中如果
有___组量相等,则它们所对应的其余各组量也相等.
中心对称
重合
顶点在圆心
弧
弦
圆心角
弦
圆心角
弧
两个圆心角
两条弧
两条弦
一
结合图形,用几何语言表述3:
①
②
③
38妇女节讲话稿:无影灯下天使情
38妇女节演讲稿:无影灯下天使情
各位领导、各位评委,来宾们,同事们:大家好!
很荣幸我能有这样的机会参加今天的演讲,我是手术室的一名普通护士。我演讲的题目是:无影灯下天使情。
记得我刚踏上手术室岗位的时候,心里充满了对新生活的美好憧憬,无影灯下,我曾用自己火样的热情和赤诚去描绘着自己未来的事业。然而,现实并不像伊甸园的菩提果那般完美和甜蜜。我每天要面对着的是一张张被病痛扭曲的面孔,听到的是一声声长吁短叹,一阵阵抽泣呜咽……永远忙碌的脚步分不清时间的分分秒秒,#个小时,#个小时,甚至##几个小时,腿酸了要站得住,肚子饿了要挺得住,眼睛困了要熬得住……多少个深夜,我们被急诊电话惊醒,不管是雷电交加或是风啸雪寒,也得从温暖的被窝爬起来,冲入沉沉的黑夜之。紧张、劳累的工作,我真正体验到了手术室护士平凡生活的滋味,体验到了其的艰辛和压力。我苦恼过、迷惘过;苦恼迷惘之后也曾动摇过、退却过。但有一件事深深地触动了我,使我从迷惘寻回了自我,在退却时坚定了初衷。
《比赛评分系统》是按照时下流行的评委打分方式设计,有比较完善的竞赛评分功能。运用互动式多媒体技术。通过投影
圆心角:
等弧:
在同圆或等圆中,能够互相重合的两条弧叫做等弧。
顶点在圆心,且与圆相交所形成的角,叫做圆心角。
弦心距:
O
C
A
B
M
圆心角:顶点在圆心的角,叫圆心角,如∠AOB .
圆心角 ∠AOB所对的弦为AB.
任意给圆心角,对应出现三个量:
圆心角
弧
弦
判一判:判别下列各图中的角是不是圆心角,并说明理由.
①
②
③
④
圆内角
圆外角
圆周角(后面会学到)
圆心角
圆心角、弧、弦、弦心距之间的关系
在等圆中
1.这两个相等的圆心角所对的弦分别是哪两条?
它们相等吗?
2.这两个相等的圆心角所对的弧分别是哪两条?
它们相等吗?
如果两个圆心角相等
叠合法
圆心角、弧、弦、弦心距之间的关系
在同圆或等圆中,
相等的圆心角所对的弧相等,
所对的弦相等。
前提条件
AB=CD ?
在同圆或等圆中,
相等的圆心角所对的弧相等,
所对的弦相等。
想一想:定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
思考:在同圆内作两条长度相同的弦,它们所对的圆心角相等吗?所对的弧相等吗?
圆心角、弧、弦、弦心距之间的关系
在同圆或等圆中,
如果两个圆心角、
两条弧、
两条弦
中有一组量相等,那么它们所对应的其余各组量都分别相等。
简称“知一推二”
或“知一推三”
三、仔细阅读课本84页例题3. 注意解题格式!
仿照例题完成课本85页练习.
(4)解:OE=OF. 理由如下,
1.判断对错:
(1)圆心角的顶点在圆心上. ( )
(2)相等的圆心角所对的弧一定相等.( )
(3)等弧所对的圆心角一定相等. ( )
(4)相等的弦所对的弧相等.( )
2.长度等于半径的弦所对的圆心角的度数为( )
A.60° B.45° C.90° D.120°
3.点A,B,C三点在☉O上,且AB=BC=AC,那么
∠AOB= ______.
4.如图,若 长为☉O周长的 ,则∠AOB=________.
5.如图,A,B是☉O上的两点,∠AOB=120°,
C是 的中点,判断四边形OACB的形状
并证明你的结论.
√
×
√
×
A
自学检测(10分钟)
120°
解:四边形OACB是菱形.理由如下:
∵C是 的中点,
∴ ∴∠AOC=∠BOC,
又∵∠AOB=120°,∴∠AOC=∠BOC=60°,
∵OA=OC,∴△AOC是等边三角形.
∴OA=OC=AC.同理可证OB=OC=BC,
∴OA=AC=CB=OB,
∴四边形OACB是菱形.
【规律总结】同一圆中证明两弦相等的“四种方法”:
1.若两弦位于两个不同的三角形,证明两弦所在的三角形全等.
2.若两弦位于同一个三角形中,根据等角对等边证明两弦相等.
3.证明两弦所对的弧相等.
4.证明两弦所对的圆心角相等.
证两条线段相等.
6.如图,以 ABCD的顶点A为圆心,AB为半径作☉A,分别交AD,BC于E,F,延长BA交☉A于G,求证:
7. 如图,在☉O中,C,D是直径AB上两点,AC=BD,MC⊥AB,
ND⊥AB,M,N在☉O上.求证:
9.如图, ⊙O中弦AB⊥AC,D,E分别是AB,AC的中点.若AB=AC,
则四边形OEAD是 形;
8.如图:已知AB、CD是⊙O两条直径,弦CE∥AB,弧EC的度数为40°,则∠BOC=______.
A
B
C
D
E
O
1100
正方形
弧的度数等于它所对的圆心角的度数.
11.如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ,则a的值是 .
A
B
O
P
x
y
y=x
E
F
H
12.如图,在⊙O中,弦AB与CD相交于点E,AB=CD.
(1)求证:△AEC≌△DEB;
(2)点B与点C关于直线OE对称吗?试说明理由.
A
B
C
D
O
E
小结(1分钟)
1.圆的对称性:
2.圆心角、弦、及弧之间相等关系的定理:
圆是轴对称图形,对称轴是任意一条过圆心的直线 ;圆是中心对称图形,对称中心为圆心.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
两条弦心距
两条弦心距
同课章节目录
