2019-2020学年粤教版必修2 1.2运动的合成与分解 达标作业(解析版)
文档属性
| 名称 | 2019-2020学年粤教版必修2 1.2运动的合成与分解 达标作业(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 210.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-16 00:00:00 | ||
图片预览



文档简介
1.2运动的合成与分解
达标作业(解析版)
1.在水平面上有A、B两物体,通过一根跨过定滑轮的轻绳相连,现A物体以v1的速度向右匀速运动,当绳被拉成与水平面的夹角分别为α、β时(如图所示),B物体的运动速度vB为(绳始终有拉力)( )
A. B.
C. D.
2.如图所示,跳伞运动员以4m/s的速度沿竖直方向匀速下降,下降一段距离后刮起了水平方向的风,最终运动员以5m/s的速度匀速运动,则此时风速大小是
A.1m/s B.3m/s
C.5m/s D.m/s
3.如图所示,有一小船正在渡河,水流速度为5m/s,在到达离对岸30m的P点时,其下游40m处有一危险水域,为了使小船在危险水域之前到达对岸,那么,小船从现在起相对于静水的最小划行速度应是多大( )
A. B. C. D.
4.一小船在静水中的速度为2v,要渡过一条宽度为d的河流,已知河水流速为v,则小船渡河( )
A.最小位移为d B.最小位移为2d
C.相对河岸最小速度为 D.相对河岸最大速度为
5.某人用绳子通过定滑轮拉物体A,A穿在光滑的竖直杆上,人以速度v0匀速向下拉绳,当物体A到达如图所示位置时,绳与竖直杆的夹角为θ,则物体A实际运动的速度是( )
A. B.
C.v0cos θ D.v0sin θ
6.河水由西向东流,河宽为800 m,河中各点的水流速度大小为v水,各点到较近河岸的距离为x,v水与x的关系为v水=x(m/s)。让小船船头垂直河岸由南向北渡河,小船划水速度大小恒为v船=4 m/s。下列说法中正确的是( )
A.小船渡河的轨迹为直线
B.小船在河水中的最大速度是5 m/s
C.小船渡河的时间是160 s
D.小船在距离南岸200 m处的速度小于距北岸200 m处的速度
7.光滑水平面上有一m=2kg的滑块以5m/s的速度向东运动,当受到一个向南大小为8N的力以后,则( )
A.物块改向东南方向做直线运动
B.1s以后物块的位移为m
C.经过很长时间物块的运动方向就会向南
D.2s后物块的运动方向为南偏东37o
8.如图所示,一条小船位于200 m宽的河正中A点处,从这里向下游100 m处有一危险区,当时水流速度为4 m/s,为了使小船避开危险区沿直线到达对岸,小船在静水中的速度至少是 ( )
A. m/s B. m/s C.2 m/s D.4 m/s
9.在抗洪抢险中,战士驾驶摩托艇救人,假设江岸是平直的,洪水沿江向下游流去,水流速度为v1,摩托艇在静水中的航速为v2,战士救人的地点A离岸边最近处O的距离为d.若战士想在最短时间内将人送上岸,则摩托艇登陆的地点离O点的距离为( )
A. B.0 C. D.
10.如图,柔软的轻绳一端系一质量为m的环,环套在竖直固定的光滑直杆上,杆上的A点与光滑的轻小定滑轮等高,杆上的B点在A点下方距离为d处。定滑轮与直杆的距离也为d,质量为2m的重物悬挂在轻绳的另一端。现将环从A处由静止释放,下列说法正确的是( )
A.环到达B处时,环与重物的速度大小相等
B.环从A到B,环减少的机械能等于重物增加的机械能
C.环到达B处时,重物上升的高度
D.环能下降的最大高度为
11.一小船渡河,河宽d=180 m,水流速度v1=2.5 m/s。若船在静水中的速度为v2=5 m/s,求:
(1)欲使船在最短的时间内渡河,船头应朝什么方向?用多长时间?位移是多少?
(2)欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?
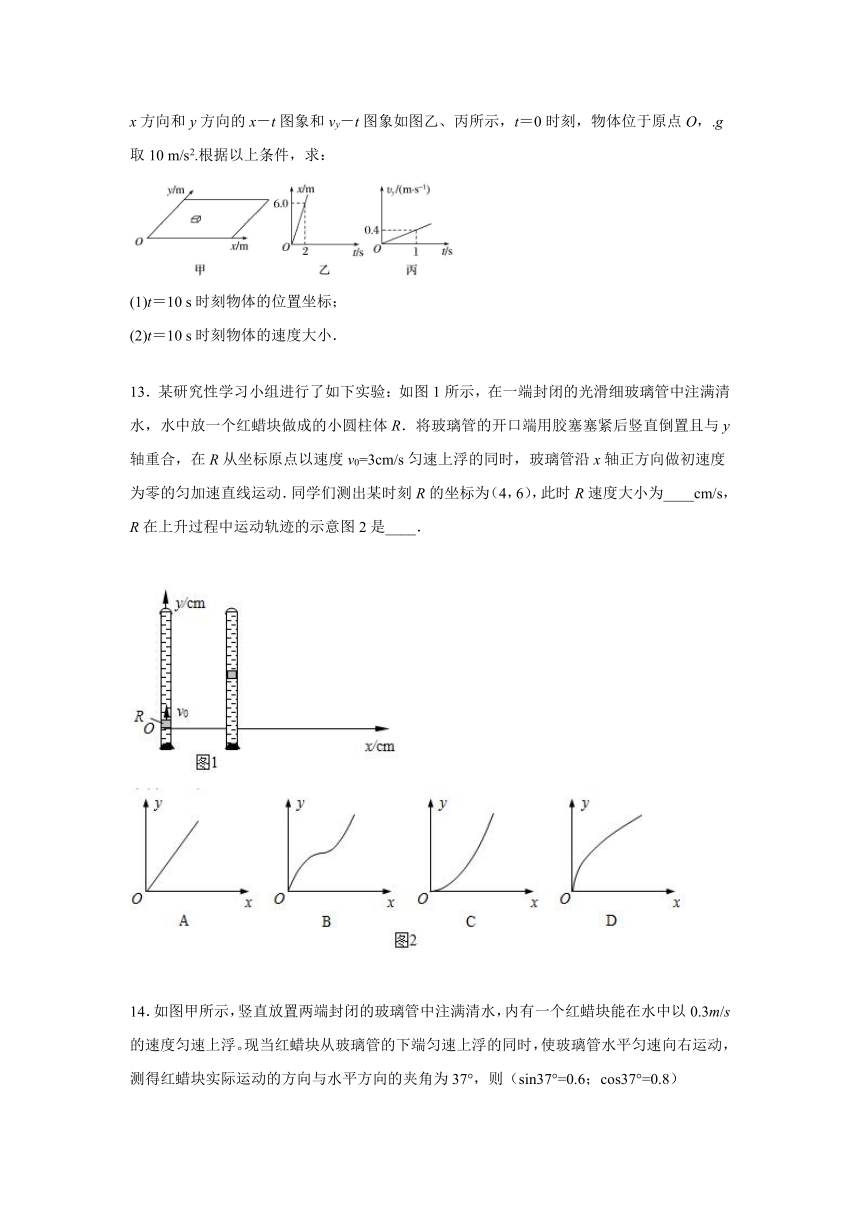
12.如图甲所示,质量m=2.0 kg的物体在水平外力的作用下在水平面上运动,已知物体沿x方向和y方向的x-t图象和vy-t图象如图乙、丙所示,t=0时刻,物体位于原点O,.g取10 m/s2.根据以上条件,求:
(1)t=10 s时刻物体的位置坐标;
(2)t=10 s时刻物体的速度大小.
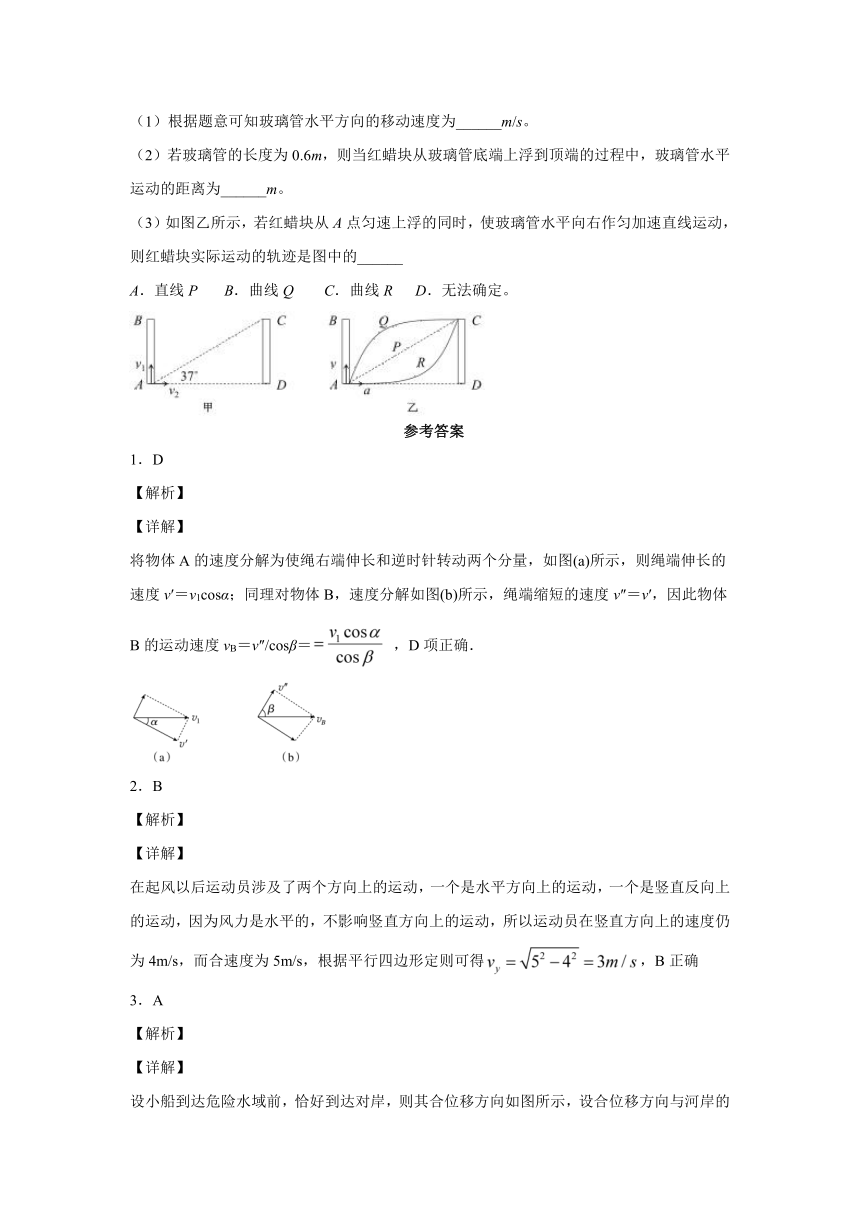
13.某研究性学习小组进行了如下实验:如图1所示,在一端封闭的光滑细玻璃管中注满清水,水中放一个红蜡块做成的小圆柱体R.将玻璃管的开口端用胶塞塞紧后竖直倒置且与y轴重合,在R从坐标原点以速度v0=3cm/s匀速上浮的同时,玻璃管沿x轴正方向做初速度为零的匀加速直线运动.同学们测出某时刻R的坐标为(4,6),此时R速度大小为____cm/s,R在上升过程中运动轨迹的示意图2是____.
14.如图甲所示,竖直放置两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.3m/s的速度匀速上浮。现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动的方向与水平方向的夹角为37°,则(sin37°=0.6;cos37°=0.8)
(1)根据题意可知玻璃管水平方向的移动速度为______m/s。
(2)若玻璃管的长度为0.6m,则当红蜡块从玻璃管底端上浮到顶端的过程中,玻璃管水平运动的距离为______m。
(3)如图乙所示,若红蜡块从A点匀速上浮的同时,使玻璃管水平向右作匀加速直线运动,则红蜡块实际运动的轨迹是图中的______
A.直线P???????B.曲线Q????????C.曲线R??????D.无法确定。
参考答案
1.D
【解析】
【详解】
将物体A的速度分解为使绳右端伸长和逆时针转动两个分量,如图(a)所示,则绳端伸长的速度v′=v1cosα;同理对物体B,速度分解如图(b)所示,绳端缩短的速度v″=v′,因此物体B的运动速度vB=v″/cosβ= ,D项正确.
2.B
【解析】
【详解】
在起风以后运动员涉及了两个方向上的运动,一个是水平方向上的运动,一个是竖直反向上的运动,因为风力是水平的,不影响竖直方向上的运动,所以运动员在竖直方向上的速度仍为4m/s,而合速度为5m/s,根据平行四边形定则可得,B正确
3.A
【解析】
【详解】
设小船到达危险水域前,恰好到达对岸,则其合位移方向如图所示,设合位移方向与河岸的夹角为α,则tanα==,即α=37°
小船的合速度方向与合位移方向相同,根据平行四边形定则知,当船相对于静水的速度?v1垂直于合速度时,v1最小,由图可知,v1的最小值为
v1min=v2sinα=5×m/s=3m/s。
A.,与结论相符,选项A正确;
B.,与结论不相符,选项B错误;
C.,与结论不相符,选项C错误;
D.,与结论不相符,选项D错误;
4.A
【解析】
【详解】
AB. 由于小船在静水中的速度为2v大于水的速度v,故小船过河最短路程为d,故A正确,B错误;
C. 两速度的合速度是相对河岸的速度,当两速度方向相反时,合速度最小,等于v,即相对河岸最小速度为v,故C错误;
D.当两速度方向一致时,合速度最大,为3v,即相对河岸最大速度为3v,故D错误.
5.A
【解析】
【详解】
将A的速度分解为沿绳子方向和垂直于绳子方向,如图所示,
拉绳子的速度等于A沿绳子方向的分速度,根据平行四边形定则得,实际速度.故A正确,BCD错误.
6.B
【解析】
【详解】
A.小船的速度为沿船头指向和顺水流方向的两个分运动的分速度的矢量和,而两个分速度垂直,故当顺水流方向的分速度最大时,合速度最大,合速度的方向随顺水流方向的分速度的变化而变化,故小船到达河中心时速度最大,且运动轨迹为曲线,故A错误;
B.当船到河中央时,水流速度达到最大,根据矢量的合成,船在河水中的最大速度
故B正确; C.将小船的运动分解为沿船头指向和顺水流方向的两个分运动,两个分运动同时发生,互不干扰,故渡河时间与顺水流方向的分运动无关,当船头与河岸垂直时,沿船头方向的分运动的分位移最小,故渡河时间最短,最短时间为
故C错误;
D.小船距南岸200m处,则水流速度为
而小船距北岸200m处时,水流速度也为1.5m/s;根据速度的合成可知,它们的速度大小相等,方向不同,故D错误;
7.B
【解析】
【详解】
A.物体在向东的方向做匀速直线运动,向南做匀加速运动,合运动为曲线运动,选项A错误;
B.向南的加速度为
1s以后向东的位移
向南的位移
则总位移:
选项B正确。
C.无论经过多长时间,物体沿正东方向总有分速度,即物块的运动方向不可能向南,选项C错误;
D.2s后物块沿向南方向的分速度
则
则运动方向为南偏东,选项D错误。
8.C
【解析】
【详解】
本题考查临界情况,小船的运动轨迹如图所示
,其中v1为船速,v2为水流速,d为河宽,x为到达危险区的距离,由此可以求出船在静水中最小速度为2 m/s,故C正确。
9.D
【解析】
根据s=vt,
因此摩托艇登陆的最短时间:
t= ,
登陆时到达O点的距离:
s=v1t=;
故选D.
点睛:摩托艇在水中一方面自己航行前进,另一方面沿水向下漂流,当摩托艇垂直于河岸方向航行时,到达岸上的时间最短,由速度公式的变形公式求出到达河岸的最短时间,然后求出摩托艇登陆的地点到O点的距离.
10.BD
【解析】
【分析】
环刚开始释放时,重物由静止开始加速。根据数学几何关系求出环到达B处时重物上升的高度。对B的速度沿绳子方向和垂直于绳子方向进行分解,在沿绳子方向上的分速度等于重物的速度,从而求出环在B处速度与重物的速度之比。环和重物组成的系统,机械能守恒。由系统的机械能守恒列式,求环能下降的最大高度.
【详解】
环到达B处时,对环B的速度沿绳子方向和垂直于绳子方向分解,在沿绳子方向上的分速度等于重物的速度,有,所以有,A错误;环下滑过程中无摩擦力做功,故系统机械能守恒,则有环减小的机械能等于重物增加的机械能,B正确;根据几何关系有,环从A下滑至B点时,下降的高度为d,则重物上升的高度,C错误;设环下滑到最大高度为h时环和重物的速度均为0,此时重物上升的最大高度为,根据系统的机械能守恒有:,解得:,D正确.
11.(1)(2)
【解析】
【详解】
(1)欲使船在最短时间内渡河,船头应朝垂直河岸方向
当船头垂直河岸时,如图甲所示;合速度为倾斜方向,垂直分速度为v2=5 m/s
t==36 s
m/s
x=vt=90m
(2)欲使船渡河航程最短,应垂直河岸渡河,船头应朝上游与垂直河岸方向成某一夹角α
如图乙所示;
有v2sin α=v1,得α=30°
所以当船头向上游偏30°时航程最短
t′==24s
x′=d=180 m
12.(1)(30m,20m)(2)5.0m/s
【解析】
【分析】
根据坐标与时间之间的关系式,代入时间即可得知该时刻对应位置的坐标;物体在两个方向上均为直线运动,所以坐标的竖直等于在该方向上的位移大小,再结合直线运动的公式,即可得知这两个方向上的速度,再对速度进行合成,可得该时刻的实际速度大小。
【详解】
(1)由图可知坐标与时间的关系为:
在x轴方向上:x=3.0t m,在y轴方向上:y=0.2t2 m
代入数据可得:t=10 s,
可得位移为:x=3.0×10m=30 m,y=0.2×102m=20m
即t=10 s时刻物体的位置坐标为(30 m,20 m)。
(2)在x轴方向上:v0=3.0 m/s
当t=10s时,vy=at=0.4×10m/s=4.0m/s
则速度为:
【点睛】
本题主要考查了对运动合成与分解的应用和物体位置的求解.要求学生要会在直角坐标系中确定物体位置,会结合位移的定理,了解位置与位移之间的联系。
13.5 D
【解析】
【详解】
[1].小圆柱体R在y轴竖直方向做匀速运动,有:
y=v0t
解得:
在x轴水平方向做初速为0的匀加速直线运动,有:
x=at2,
解得:
那么R的速度大小:
[2].因合外力沿x轴,由合外力指向曲线弯曲的内侧来判断轨迹示意图是D.
14.0.4 0.8 B
【解析】
【详解】
解:(1)根据平行四边形定则,有:
则有:
(2)在竖直方向上运动的时间为:
则玻璃管在水平方向上运动的距离为:
(3)根据运动的合成与分解,运动的轨迹偏向合外力的方向,则有Q,故选项B正确,A、C、D错误。
达标作业(解析版)
1.在水平面上有A、B两物体,通过一根跨过定滑轮的轻绳相连,现A物体以v1的速度向右匀速运动,当绳被拉成与水平面的夹角分别为α、β时(如图所示),B物体的运动速度vB为(绳始终有拉力)( )
A. B.
C. D.
2.如图所示,跳伞运动员以4m/s的速度沿竖直方向匀速下降,下降一段距离后刮起了水平方向的风,最终运动员以5m/s的速度匀速运动,则此时风速大小是
A.1m/s B.3m/s
C.5m/s D.m/s
3.如图所示,有一小船正在渡河,水流速度为5m/s,在到达离对岸30m的P点时,其下游40m处有一危险水域,为了使小船在危险水域之前到达对岸,那么,小船从现在起相对于静水的最小划行速度应是多大( )
A. B. C. D.
4.一小船在静水中的速度为2v,要渡过一条宽度为d的河流,已知河水流速为v,则小船渡河( )
A.最小位移为d B.最小位移为2d
C.相对河岸最小速度为 D.相对河岸最大速度为
5.某人用绳子通过定滑轮拉物体A,A穿在光滑的竖直杆上,人以速度v0匀速向下拉绳,当物体A到达如图所示位置时,绳与竖直杆的夹角为θ,则物体A实际运动的速度是( )
A. B.
C.v0cos θ D.v0sin θ
6.河水由西向东流,河宽为800 m,河中各点的水流速度大小为v水,各点到较近河岸的距离为x,v水与x的关系为v水=x(m/s)。让小船船头垂直河岸由南向北渡河,小船划水速度大小恒为v船=4 m/s。下列说法中正确的是( )
A.小船渡河的轨迹为直线
B.小船在河水中的最大速度是5 m/s
C.小船渡河的时间是160 s
D.小船在距离南岸200 m处的速度小于距北岸200 m处的速度
7.光滑水平面上有一m=2kg的滑块以5m/s的速度向东运动,当受到一个向南大小为8N的力以后,则( )
A.物块改向东南方向做直线运动
B.1s以后物块的位移为m
C.经过很长时间物块的运动方向就会向南
D.2s后物块的运动方向为南偏东37o
8.如图所示,一条小船位于200 m宽的河正中A点处,从这里向下游100 m处有一危险区,当时水流速度为4 m/s,为了使小船避开危险区沿直线到达对岸,小船在静水中的速度至少是 ( )
A. m/s B. m/s C.2 m/s D.4 m/s
9.在抗洪抢险中,战士驾驶摩托艇救人,假设江岸是平直的,洪水沿江向下游流去,水流速度为v1,摩托艇在静水中的航速为v2,战士救人的地点A离岸边最近处O的距离为d.若战士想在最短时间内将人送上岸,则摩托艇登陆的地点离O点的距离为( )
A. B.0 C. D.
10.如图,柔软的轻绳一端系一质量为m的环,环套在竖直固定的光滑直杆上,杆上的A点与光滑的轻小定滑轮等高,杆上的B点在A点下方距离为d处。定滑轮与直杆的距离也为d,质量为2m的重物悬挂在轻绳的另一端。现将环从A处由静止释放,下列说法正确的是( )
A.环到达B处时,环与重物的速度大小相等
B.环从A到B,环减少的机械能等于重物增加的机械能
C.环到达B处时,重物上升的高度
D.环能下降的最大高度为
11.一小船渡河,河宽d=180 m,水流速度v1=2.5 m/s。若船在静水中的速度为v2=5 m/s,求:
(1)欲使船在最短的时间内渡河,船头应朝什么方向?用多长时间?位移是多少?
(2)欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?
12.如图甲所示,质量m=2.0 kg的物体在水平外力的作用下在水平面上运动,已知物体沿x方向和y方向的x-t图象和vy-t图象如图乙、丙所示,t=0时刻,物体位于原点O,.g取10 m/s2.根据以上条件,求:
(1)t=10 s时刻物体的位置坐标;
(2)t=10 s时刻物体的速度大小.
13.某研究性学习小组进行了如下实验:如图1所示,在一端封闭的光滑细玻璃管中注满清水,水中放一个红蜡块做成的小圆柱体R.将玻璃管的开口端用胶塞塞紧后竖直倒置且与y轴重合,在R从坐标原点以速度v0=3cm/s匀速上浮的同时,玻璃管沿x轴正方向做初速度为零的匀加速直线运动.同学们测出某时刻R的坐标为(4,6),此时R速度大小为____cm/s,R在上升过程中运动轨迹的示意图2是____.
14.如图甲所示,竖直放置两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.3m/s的速度匀速上浮。现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动的方向与水平方向的夹角为37°,则(sin37°=0.6;cos37°=0.8)
(1)根据题意可知玻璃管水平方向的移动速度为______m/s。
(2)若玻璃管的长度为0.6m,则当红蜡块从玻璃管底端上浮到顶端的过程中,玻璃管水平运动的距离为______m。
(3)如图乙所示,若红蜡块从A点匀速上浮的同时,使玻璃管水平向右作匀加速直线运动,则红蜡块实际运动的轨迹是图中的______
A.直线P???????B.曲线Q????????C.曲线R??????D.无法确定。
参考答案
1.D
【解析】
【详解】
将物体A的速度分解为使绳右端伸长和逆时针转动两个分量,如图(a)所示,则绳端伸长的速度v′=v1cosα;同理对物体B,速度分解如图(b)所示,绳端缩短的速度v″=v′,因此物体B的运动速度vB=v″/cosβ= ,D项正确.
2.B
【解析】
【详解】
在起风以后运动员涉及了两个方向上的运动,一个是水平方向上的运动,一个是竖直反向上的运动,因为风力是水平的,不影响竖直方向上的运动,所以运动员在竖直方向上的速度仍为4m/s,而合速度为5m/s,根据平行四边形定则可得,B正确
3.A
【解析】
【详解】
设小船到达危险水域前,恰好到达对岸,则其合位移方向如图所示,设合位移方向与河岸的夹角为α,则tanα==,即α=37°
小船的合速度方向与合位移方向相同,根据平行四边形定则知,当船相对于静水的速度?v1垂直于合速度时,v1最小,由图可知,v1的最小值为
v1min=v2sinα=5×m/s=3m/s。
A.,与结论相符,选项A正确;
B.,与结论不相符,选项B错误;
C.,与结论不相符,选项C错误;
D.,与结论不相符,选项D错误;
4.A
【解析】
【详解】
AB. 由于小船在静水中的速度为2v大于水的速度v,故小船过河最短路程为d,故A正确,B错误;
C. 两速度的合速度是相对河岸的速度,当两速度方向相反时,合速度最小,等于v,即相对河岸最小速度为v,故C错误;
D.当两速度方向一致时,合速度最大,为3v,即相对河岸最大速度为3v,故D错误.
5.A
【解析】
【详解】
将A的速度分解为沿绳子方向和垂直于绳子方向,如图所示,
拉绳子的速度等于A沿绳子方向的分速度,根据平行四边形定则得,实际速度.故A正确,BCD错误.
6.B
【解析】
【详解】
A.小船的速度为沿船头指向和顺水流方向的两个分运动的分速度的矢量和,而两个分速度垂直,故当顺水流方向的分速度最大时,合速度最大,合速度的方向随顺水流方向的分速度的变化而变化,故小船到达河中心时速度最大,且运动轨迹为曲线,故A错误;
B.当船到河中央时,水流速度达到最大,根据矢量的合成,船在河水中的最大速度
故B正确; C.将小船的运动分解为沿船头指向和顺水流方向的两个分运动,两个分运动同时发生,互不干扰,故渡河时间与顺水流方向的分运动无关,当船头与河岸垂直时,沿船头方向的分运动的分位移最小,故渡河时间最短,最短时间为
故C错误;
D.小船距南岸200m处,则水流速度为
而小船距北岸200m处时,水流速度也为1.5m/s;根据速度的合成可知,它们的速度大小相等,方向不同,故D错误;
7.B
【解析】
【详解】
A.物体在向东的方向做匀速直线运动,向南做匀加速运动,合运动为曲线运动,选项A错误;
B.向南的加速度为
1s以后向东的位移
向南的位移
则总位移:
选项B正确。
C.无论经过多长时间,物体沿正东方向总有分速度,即物块的运动方向不可能向南,选项C错误;
D.2s后物块沿向南方向的分速度
则
则运动方向为南偏东,选项D错误。
8.C
【解析】
【详解】
本题考查临界情况,小船的运动轨迹如图所示
,其中v1为船速,v2为水流速,d为河宽,x为到达危险区的距离,由此可以求出船在静水中最小速度为2 m/s,故C正确。
9.D
【解析】
根据s=vt,
因此摩托艇登陆的最短时间:
t= ,
登陆时到达O点的距离:
s=v1t=;
故选D.
点睛:摩托艇在水中一方面自己航行前进,另一方面沿水向下漂流,当摩托艇垂直于河岸方向航行时,到达岸上的时间最短,由速度公式的变形公式求出到达河岸的最短时间,然后求出摩托艇登陆的地点到O点的距离.
10.BD
【解析】
【分析】
环刚开始释放时,重物由静止开始加速。根据数学几何关系求出环到达B处时重物上升的高度。对B的速度沿绳子方向和垂直于绳子方向进行分解,在沿绳子方向上的分速度等于重物的速度,从而求出环在B处速度与重物的速度之比。环和重物组成的系统,机械能守恒。由系统的机械能守恒列式,求环能下降的最大高度.
【详解】
环到达B处时,对环B的速度沿绳子方向和垂直于绳子方向分解,在沿绳子方向上的分速度等于重物的速度,有,所以有,A错误;环下滑过程中无摩擦力做功,故系统机械能守恒,则有环减小的机械能等于重物增加的机械能,B正确;根据几何关系有,环从A下滑至B点时,下降的高度为d,则重物上升的高度,C错误;设环下滑到最大高度为h时环和重物的速度均为0,此时重物上升的最大高度为,根据系统的机械能守恒有:,解得:,D正确.
11.(1)(2)
【解析】
【详解】
(1)欲使船在最短时间内渡河,船头应朝垂直河岸方向
当船头垂直河岸时,如图甲所示;合速度为倾斜方向,垂直分速度为v2=5 m/s
t==36 s
m/s
x=vt=90m
(2)欲使船渡河航程最短,应垂直河岸渡河,船头应朝上游与垂直河岸方向成某一夹角α
如图乙所示;
有v2sin α=v1,得α=30°
所以当船头向上游偏30°时航程最短
t′==24s
x′=d=180 m
12.(1)(30m,20m)(2)5.0m/s
【解析】
【分析】
根据坐标与时间之间的关系式,代入时间即可得知该时刻对应位置的坐标;物体在两个方向上均为直线运动,所以坐标的竖直等于在该方向上的位移大小,再结合直线运动的公式,即可得知这两个方向上的速度,再对速度进行合成,可得该时刻的实际速度大小。
【详解】
(1)由图可知坐标与时间的关系为:
在x轴方向上:x=3.0t m,在y轴方向上:y=0.2t2 m
代入数据可得:t=10 s,
可得位移为:x=3.0×10m=30 m,y=0.2×102m=20m
即t=10 s时刻物体的位置坐标为(30 m,20 m)。
(2)在x轴方向上:v0=3.0 m/s
当t=10s时,vy=at=0.4×10m/s=4.0m/s
则速度为:
【点睛】
本题主要考查了对运动合成与分解的应用和物体位置的求解.要求学生要会在直角坐标系中确定物体位置,会结合位移的定理,了解位置与位移之间的联系。
13.5 D
【解析】
【详解】
[1].小圆柱体R在y轴竖直方向做匀速运动,有:
y=v0t
解得:
在x轴水平方向做初速为0的匀加速直线运动,有:
x=at2,
解得:
那么R的速度大小:
[2].因合外力沿x轴,由合外力指向曲线弯曲的内侧来判断轨迹示意图是D.
14.0.4 0.8 B
【解析】
【详解】
解:(1)根据平行四边形定则,有:
则有:
(2)在竖直方向上运动的时间为:
则玻璃管在水平方向上运动的距离为:
(3)根据运动的合成与分解,运动的轨迹偏向合外力的方向,则有Q,故选项B正确,A、C、D错误。
同课章节目录
- 第一章 抛体运动
- 第01节 什么是抛体运动
- 第02节 运动的合成与分解
- 第03节 竖直方向的抛体运动
- 第04节 平抛运动
- 第05节 斜抛运动
- 第二章 圆周运动
- 第01节 匀速圆周运动
- 第02节 向心力
- 第03节 离心现象及其应用
- 第三章 万有引力定律及其应用
- 第01节 万有引力定律
- 第02节 万有引力定律的应用
- 第03节 飞向太空
- 第四章 机械能和能源
- 第01节 功
- 第02节 动能 势能
- 第03节 探究外力做功与物体动能变化的关系
- 第04节 机械能守恒定律
- 第05节 验证机械能守恒定律
- 第06节 能量 能量转化与守恒定律
- 第07节 功率
- 第08节 能源的开发与利用
- 第五章 经典力学与物理学的革命
- 第01节 经典力学的成就与局限性
- 第02节 经典时空观与相对论时空观
- 第03节 量子化现象
- 第04节 物理学——人类文明进步的阶梯
