北师大版八年级数学下册6.3三角形的中位线课件(共47张PPT)
文档属性
| 名称 | 北师大版八年级数学下册6.3三角形的中位线课件(共47张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-16 22:46:27 | ||
图片预览






文档简介
(共47张PPT)
第六章 平行四边形
6.3 三角形的中位线
【复习回顾】
平行四边形的性质与判定
平行四边形的①两组对边分别平行②两组对边分别相等
平行四边形的①对角相等②邻角互补
平行四边形的对角线互相平分
夹在两条平行线间的平行线段相等
①两组对边分别平行的四边形
②两组对边分别相等的四边形
③一组对边平行且相等的四边形
两组对角分别相等的四边形
对角线互相平分四边形
性质 判定
边
角
对角线
推论
【新课导入】
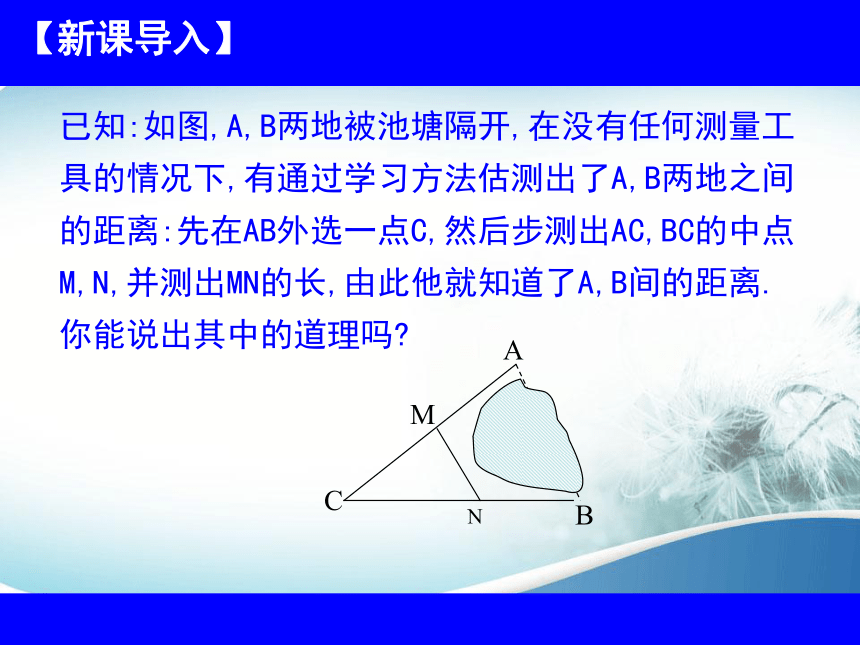
已知:如图,A,B两地被池塘隔开,在没有任何测量工具的情况下,有通过学习方法估测出了A,B两地之间的距离:先在AB外选一点C,然后步测出AC,BC的中点M,N,并测出MN的长,由此他就知道了A,B间的距离.你能说出其中的道理吗?
【概念解析】
连接三角形两边中点的线段,叫做三角形的中位线
三角形中位线定义:
AF是△ABC的中线
DE是△ABC 的中位线
C
B
A
F
E
D
注意概念区分:三角形中线
【概念解析】
理解三角形的中位线定义的两层含义:
② 如果DE为△ABC的中位线,那么
D、E分别为AB、AC的 。
① 如果D、E分别为AB、AC的中点,
那么DE为△ABC的 ;
中位线
中点
C
B
A
E
D
【新课探究】
你能将任意一个三角形分成四个全等的三角形吗?
连接每两边的中点,看看得到了什么
样的图形?
四个全等的三角形.
请你设法验证上面的结论,
你敢应战吗?
猜一猜,三角形中位线有什么性质?
做做想想
【合作探究】
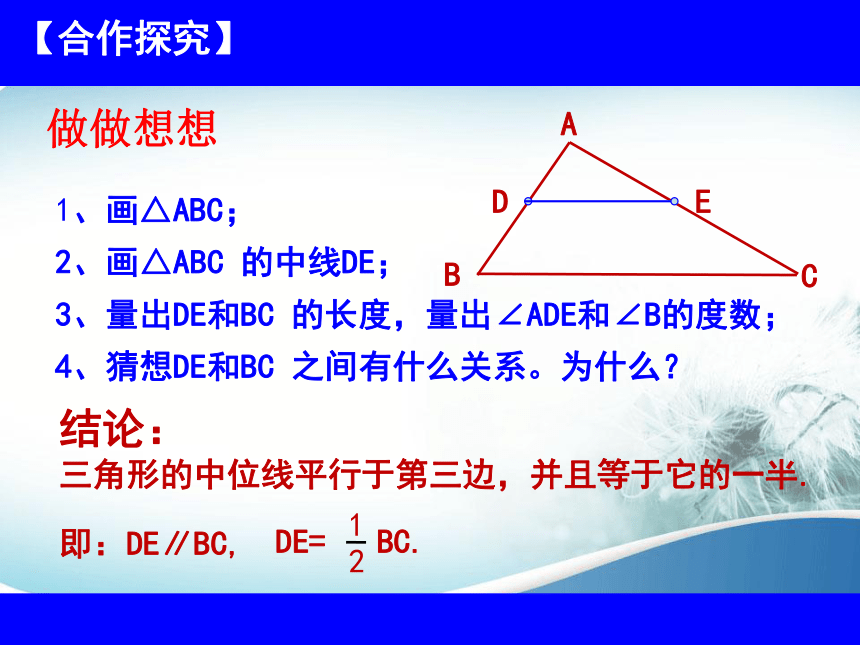
1、画△ABC;
2、画△ABC 的中线DE;
3、量出DE和BC 的长度,量出∠ADE和∠B的度数;
4、猜想DE和BC 之间有什么关系。为什么?
做做想想
结论:
三角形的中位线平行于第三边,并且等于它的一半.
A
B
C
D
E
【合作探究】
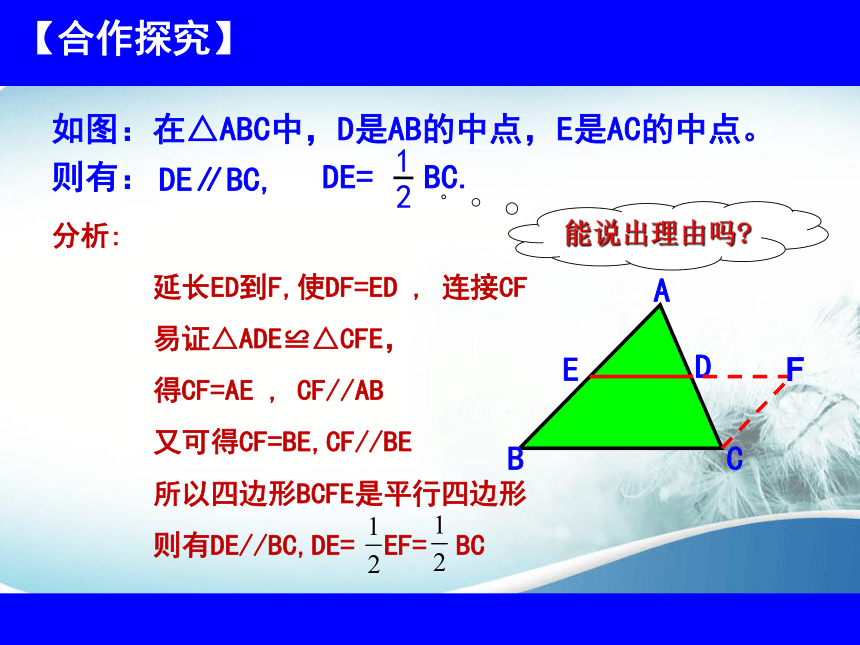
如图:在△ABC中,D是AB的中点,E是AC的中点。
则有:
DE∥BC,
能说出理由吗?
分析:
延长ED到F,使DF=ED , 连接CF
易证△ADE≌△CFE,
得CF=AE , CF//AB
又可得CF=BE,CF//BE
所以四边形BCFE是平行四边形
则有DE//BC,DE= EF= BC
【典例精析】
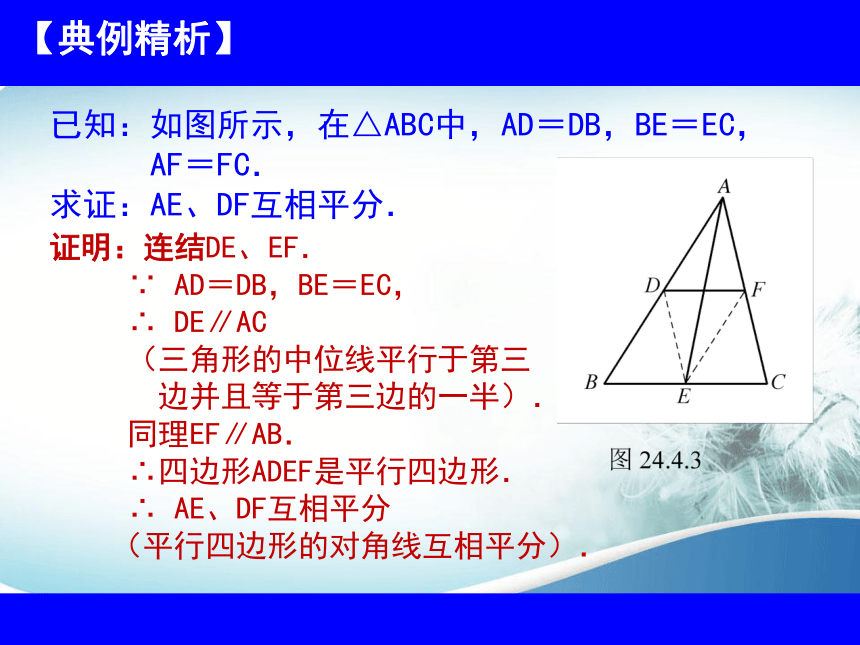
已知:如图所示,在△ABC中,AD=DB,BE=EC,
AF=FC.
求证:AE、DF互相平分.
证明:连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC
(三角形的中位线平行于第三
边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分
(平行四边形的对角线互相平分).
【典例精析】
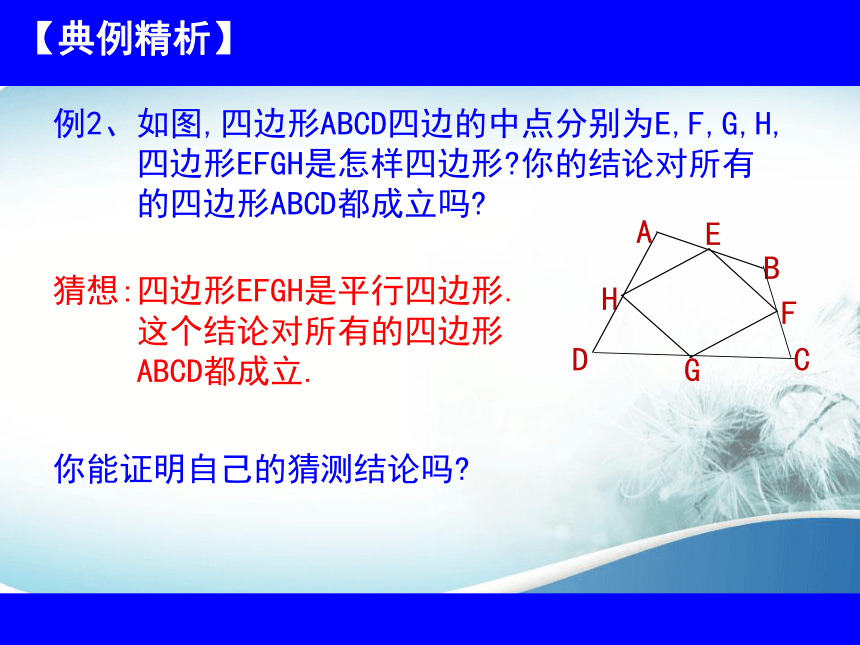
例2、如图,四边形ABCD四边的中点分别为E,F,G,H,
四边形EFGH是怎样四边形?你的结论对所有
的四边形ABCD都成立吗?
猜想:四边形EFGH是平行四边形.
这个结论对所有的四边形
ABCD都成立.
你能证明自己的猜测结论吗?
【典例探究】
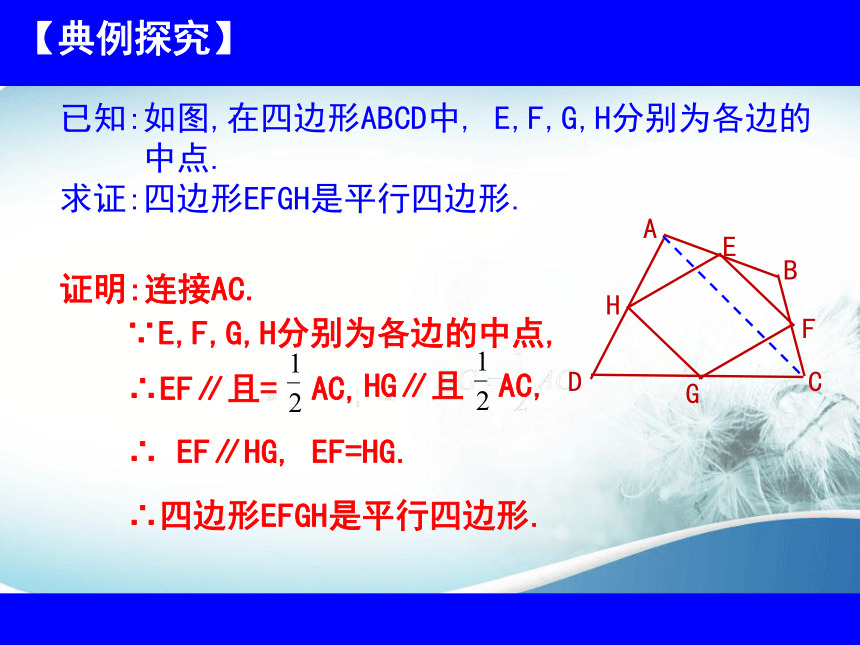
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴四边形EFGH是平行四边形.
求证:四边形EFGH是平行四边形.
已知:如图,在四边形ABCD中, E,F,G,H分别为各边的
中点.
【合作探究】
从例2中你能得到什么结论?
顺次连接四边形各边中点的线段组成一个平行四边形
猜测:
顺次连接矩形各边中点的线段组成一个
菱形
【课堂小练】
(1)?顺次连结平行四边形各边中点所得的四边形是什么?
(2)顺次连结菱形各边中点所得的四边形是什么?
平行四边形
矩形
(3)顺次连结正方形各边中点所得的四边形是什么?
正方形
【课堂小练】
(4)顺次连结梯形各边中点所得的四边形是什么?
(5)顺次连结等腰梯形各边中点所得的四边形是什么?
平行四边形
菱形
【课堂小练】
顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于什么呢?
【课堂小练】
(6)顺次连结对角线相等的四边形各边中点所得的四边形是什么?
(8)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么?
(7)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
菱形
矩形
正方形
【重要结论】
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
原四边形两条对角线 连接四边中点所得四边形
【课堂小练】
【课堂小练】
1、顺次连接四边形各边中点得到的是
【课堂小练】
2、顺次连接矩形各边中点得到的是
【课堂小练】
3、顺次连接菱形各边中点得到的是
【课堂小练】
4、顺次连接四边形各边中点得到正方形,那么这个
四边形是
【课堂小练】
5、顺次连接四边形各边中点得到菱形,那么这个四
边形是
【课堂小练】
6、顺次连接对角线互相平分的四边形各边中点得到
的是
【课堂小练】
7、顺次连接对角线互相垂直的四边形各边中点得到
的是
【课堂小练】
8、顺次连接对角线相等的四边形各边中点得到
的是
【课堂小练】
【课堂小练】
真聪明!
返 回
【课堂小练】
错了!请重新返回思考一下 !
返 回
【课堂小练】
你真聪明!
返 回
【课堂小练】
请你慎重选择!返回再思考
返 回
【课堂小练】
返 回
【课堂小练】
错啦!仔细考虑一下
返 回
【课堂小练】
很好!继续保持
返 回
【课堂小练】
错了!好好思考
返 回
【课堂小练】
真聪明!继续努力
返 回
【课堂小练】
答错了!再想想吧
返 回
【课堂小练】
真聪明!
返 回
【课堂小练】
答错了!
返 回
【课堂小练】
真聪明!
返 回
【课堂小练】
返 回
错啦!仔细考虑一下
【课堂小练】
真的太厉害了!
返 回
【课堂小练】
返 回
错了!好好思考
【课堂小练】
三角形各边的长分别为6 cm、8 cm 和 10 cm ,求连接各边中点所成三角形的周长=
AB=10 cm
BC=8 cm
AC=6 cm
EF=5 cm
DF=4 cm
DE=3 cm
12 cm
【挑战自我】
理由:
∵ 点E,F分别为BC,AC的中点
∴ EF ∥AB,EF=1/2AB
∴ ∠DAC= ∠EFC=90 °
∵ AD=1/2AB,
∴ AD=EF,
∵ AF=CF,
∴ △ADF≌ △FEC (SAS)
∴ DF=EC
∵ BE=EC, ∴ DF=BE
在△ABC中,∠BAC=90°,延长BA到点D,使AD=1/2AB,点E,F分别为BC,AC的中点,试说DF=BE理由
还有其他做法吗?
提示:连接AE
【课堂小练】
1.三角形的中位线定义.
2.三角形的中位线定理.
3.三角形的中位线定理不仅给出了中位线与第三边
的关系,而且给出了他们的数量关系,在三角形
中给出一边的中点时,要转化为中位线.
4.线段的倍分要转化为相等问题来解决.
5.三角形的中位线定理的发现过程所用到的数学方
法(包括画图、实验、猜想、分析、归纳等.)
【作业布置】
课内作业:
1、随堂练习
2、学习手册
课外作业
3、测量金海湾钟楼的底面对角线的长
第六章 平行四边形
6.3 三角形的中位线
【复习回顾】
平行四边形的性质与判定
平行四边形的①两组对边分别平行②两组对边分别相等
平行四边形的①对角相等②邻角互补
平行四边形的对角线互相平分
夹在两条平行线间的平行线段相等
①两组对边分别平行的四边形
②两组对边分别相等的四边形
③一组对边平行且相等的四边形
两组对角分别相等的四边形
对角线互相平分四边形
性质 判定
边
角
对角线
推论
【新课导入】
已知:如图,A,B两地被池塘隔开,在没有任何测量工具的情况下,有通过学习方法估测出了A,B两地之间的距离:先在AB外选一点C,然后步测出AC,BC的中点M,N,并测出MN的长,由此他就知道了A,B间的距离.你能说出其中的道理吗?
【概念解析】
连接三角形两边中点的线段,叫做三角形的中位线
三角形中位线定义:
AF是△ABC的中线
DE是△ABC 的中位线
C
B
A
F
E
D
注意概念区分:三角形中线
【概念解析】
理解三角形的中位线定义的两层含义:
② 如果DE为△ABC的中位线,那么
D、E分别为AB、AC的 。
① 如果D、E分别为AB、AC的中点,
那么DE为△ABC的 ;
中位线
中点
C
B
A
E
D
【新课探究】
你能将任意一个三角形分成四个全等的三角形吗?
连接每两边的中点,看看得到了什么
样的图形?
四个全等的三角形.
请你设法验证上面的结论,
你敢应战吗?
猜一猜,三角形中位线有什么性质?
做做想想
【合作探究】
1、画△ABC;
2、画△ABC 的中线DE;
3、量出DE和BC 的长度,量出∠ADE和∠B的度数;
4、猜想DE和BC 之间有什么关系。为什么?
做做想想
结论:
三角形的中位线平行于第三边,并且等于它的一半.
A
B
C
D
E
【合作探究】
如图:在△ABC中,D是AB的中点,E是AC的中点。
则有:
DE∥BC,
能说出理由吗?
分析:
延长ED到F,使DF=ED , 连接CF
易证△ADE≌△CFE,
得CF=AE , CF//AB
又可得CF=BE,CF//BE
所以四边形BCFE是平行四边形
则有DE//BC,DE= EF= BC
【典例精析】
已知:如图所示,在△ABC中,AD=DB,BE=EC,
AF=FC.
求证:AE、DF互相平分.
证明:连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC
(三角形的中位线平行于第三
边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分
(平行四边形的对角线互相平分).
【典例精析】
例2、如图,四边形ABCD四边的中点分别为E,F,G,H,
四边形EFGH是怎样四边形?你的结论对所有
的四边形ABCD都成立吗?
猜想:四边形EFGH是平行四边形.
这个结论对所有的四边形
ABCD都成立.
你能证明自己的猜测结论吗?
【典例探究】
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴四边形EFGH是平行四边形.
求证:四边形EFGH是平行四边形.
已知:如图,在四边形ABCD中, E,F,G,H分别为各边的
中点.
【合作探究】
从例2中你能得到什么结论?
顺次连接四边形各边中点的线段组成一个平行四边形
猜测:
顺次连接矩形各边中点的线段组成一个
菱形
【课堂小练】
(1)?顺次连结平行四边形各边中点所得的四边形是什么?
(2)顺次连结菱形各边中点所得的四边形是什么?
平行四边形
矩形
(3)顺次连结正方形各边中点所得的四边形是什么?
正方形
【课堂小练】
(4)顺次连结梯形各边中点所得的四边形是什么?
(5)顺次连结等腰梯形各边中点所得的四边形是什么?
平行四边形
菱形
【课堂小练】
顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于什么呢?
【课堂小练】
(6)顺次连结对角线相等的四边形各边中点所得的四边形是什么?
(8)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么?
(7)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
菱形
矩形
正方形
【重要结论】
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
原四边形两条对角线 连接四边中点所得四边形
【课堂小练】
【课堂小练】
1、顺次连接四边形各边中点得到的是
【课堂小练】
2、顺次连接矩形各边中点得到的是
【课堂小练】
3、顺次连接菱形各边中点得到的是
【课堂小练】
4、顺次连接四边形各边中点得到正方形,那么这个
四边形是
【课堂小练】
5、顺次连接四边形各边中点得到菱形,那么这个四
边形是
【课堂小练】
6、顺次连接对角线互相平分的四边形各边中点得到
的是
【课堂小练】
7、顺次连接对角线互相垂直的四边形各边中点得到
的是
【课堂小练】
8、顺次连接对角线相等的四边形各边中点得到
的是
【课堂小练】
【课堂小练】
真聪明!
返 回
【课堂小练】
错了!请重新返回思考一下 !
返 回
【课堂小练】
你真聪明!
返 回
【课堂小练】
请你慎重选择!返回再思考
返 回
【课堂小练】
返 回
【课堂小练】
错啦!仔细考虑一下
返 回
【课堂小练】
很好!继续保持
返 回
【课堂小练】
错了!好好思考
返 回
【课堂小练】
真聪明!继续努力
返 回
【课堂小练】
答错了!再想想吧
返 回
【课堂小练】
真聪明!
返 回
【课堂小练】
答错了!
返 回
【课堂小练】
真聪明!
返 回
【课堂小练】
返 回
错啦!仔细考虑一下
【课堂小练】
真的太厉害了!
返 回
【课堂小练】
返 回
错了!好好思考
【课堂小练】
三角形各边的长分别为6 cm、8 cm 和 10 cm ,求连接各边中点所成三角形的周长=
AB=10 cm
BC=8 cm
AC=6 cm
EF=5 cm
DF=4 cm
DE=3 cm
12 cm
【挑战自我】
理由:
∵ 点E,F分别为BC,AC的中点
∴ EF ∥AB,EF=1/2AB
∴ ∠DAC= ∠EFC=90 °
∵ AD=1/2AB,
∴ AD=EF,
∵ AF=CF,
∴ △ADF≌ △FEC (SAS)
∴ DF=EC
∵ BE=EC, ∴ DF=BE
在△ABC中,∠BAC=90°,延长BA到点D,使AD=1/2AB,点E,F分别为BC,AC的中点,试说DF=BE理由
还有其他做法吗?
提示:连接AE
【课堂小练】
1.三角形的中位线定义.
2.三角形的中位线定理.
3.三角形的中位线定理不仅给出了中位线与第三边
的关系,而且给出了他们的数量关系,在三角形
中给出一边的中点时,要转化为中位线.
4.线段的倍分要转化为相等问题来解决.
5.三角形的中位线定理的发现过程所用到的数学方
法(包括画图、实验、猜想、分析、归纳等.)
【作业布置】
课内作业:
1、随堂练习
2、学习手册
课外作业
3、测量金海湾钟楼的底面对角线的长
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
