五年级上册数学单元测试-6.多边形的面积 人教新版(含答案)
文档属性
| 名称 | 五年级上册数学单元测试-6.多边形的面积 人教新版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 85.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-17 19:13:40 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级上册数学单元测试-6.多边形的面积
一、单选题
1.下面三幅图中,正方形一样大,则三个阴影部分的面积(??? )
A.?一样大??????????????????????B.?第一幅图最大??????????????????????C.?第二幅图最大??????????????????????D.?第三幅图最大
2.如图平行四边形中有A、B、C三个三角形(阴影部分),关于这三个三角形面积之间的关系,下面关系式正确的是( ??)。
A.?A>B+C???????????????????????????????????B.?A=B+C???????????????????????????????????C.?A<B+C
3.如图,AD=DC,AE=EB.若阴影部分的面积是20,则三角形ABC的面积是(? ??)cm2 .
A.?40????????????????????????????????????????B.?60????????????????????????????????????????C.?80????????????????????????????????????????D.?100
4.把一块三角形的地画在比例尺是1:500的图纸上,量得图上三角形的底是12厘米,高8厘米,这块地实际面积是( )
A.?480平方米???????????????????????????????B.?240平方米???????????????????????????????C.?1200平方米
二、判断题
5.面积相同的两个梯形,形状完全相同。
6.判断对错.
如果两个平行四边形的面积相等,那么它们的底和高也一定相等.
7.三角形的底一定,它的面积和高成正比例.(?? )
8.梯形上下底的和与三角形的底相等时,它们的面积相等,高一定相等
三、填空题
9.任意一个平行四边形可以转化成一个________相等的长方形,这个长方形的长与平行四边形的________相等,宽与平行四边形的________相等,所以平行四边形的面积=________×________,用字母表示为________。
10.两个完全一样的梯形拼成一个平行四边形,这个平行四边形的底为24cm,高为20cm。每个梯形的面积是________cm2。
11.把一个平行四边形木条框架拉成长方形,周长________,面积________。
A.变大????????? ?B.变小 ?????????C.不变
12.一个梯形果园的上底与下底的和是160米,高是45米,这个果园的面积是________平方米.如果按每8平方米种一棵果树计算,这个果园一共可以种果树________棵.
13.三角形的面积是________
四、解答题
14.下面是一面墙,中间有一个长2米、宽1.5米的窗户,如果砌这面墙,平均每平方米用砖160块,一共用砖多少块?
15.画一画,量一量,算一算下列图形的面积。(测量精确到毫米。)
(1)
(2)
(3)
五、综合题
16.一个近似平行四边形的花坛,底是40米,高18米。在这个花坛里按株距是0.8米、行距是0.5米栽月季花。
(1)这个花坛能栽月季花________棵.
(2)购买月季花每株需要2.3元,一共需要________元。
六、应用题
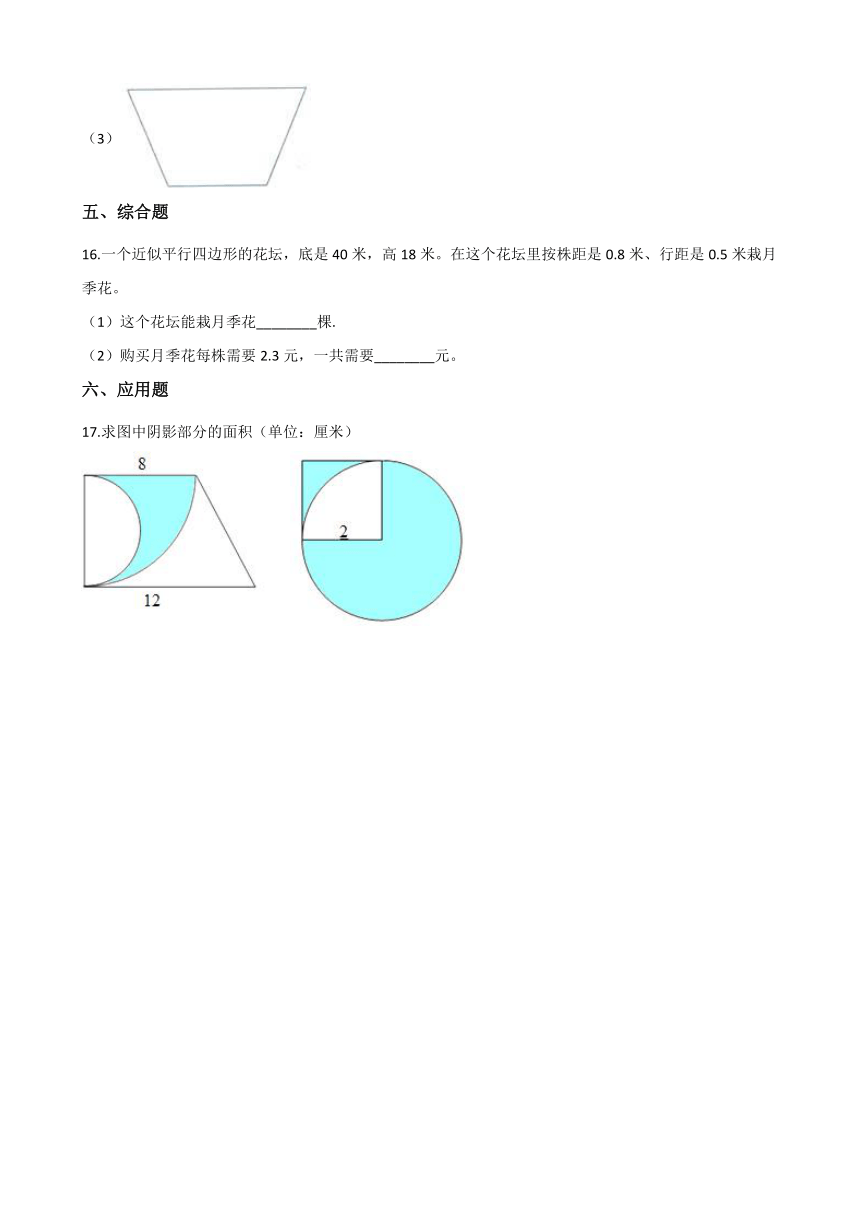
17.求图中阴影部分的面积(单位:厘米)
参考答案
一、单选题
1.【答案】 A
【解析】【解答】假设正方形的边长是4,
第一个图形:
4×4-3.14×(4÷2)?
=16-3.14×4
=16-12.56
=3.44
第二个图形:
4×4-3.14×(4÷4)?×4
=16-3.14×4
=16-12.56
=3.44
第三个图形:
4×4-3.14×4?÷4
=16-3.14×4
=16-12.56
=3.44
所以三个阴影部分的面积一样大.
故答案为:A
【分析】三个阴影部分的面积都是正方形面积减去内部空白部分的面积,假设出正方形的边长,然后根据正方形和圆面积公式分别计算阴影部分的面积并作出判断即可.
2.【答案】 B
【解析】【解答】解:A+D=B+C+D,所以A=B+C
故答案为:B
【分析】A和D组成的三角形与B、C、D组成的三角形都是平行四边形面积的一半,因此面积和相等,这样就能判断A、B、C三部分之间的关系。
3.【答案】 C
【解析】【解答】解:如图,AD=DC,AE=EB.若阴影部分的面积是20,则三角形ABC的面积是80cm2。
故答案为:C。
【分析】根据三角形的面积公式,三角形ADE的面积=三角形CDE的面积=20cm2 , 三角形ACE的面积=三角形BCE的面积=40cm2 , 所以三角形ABC的面积是80cm2。
4.【答案】C
【解析】【解答】解:设实际的底是x厘米,实际的高是y厘米,
1:500=12:x
x=500×12
x=6000;
1:500=8:y
y=8×500
y=4000;
实际面积:6000×4000× =12000000(平分厘米);
12000000平分厘米=1200平方米;
答:这块地的实际面积是1200平方米.
故选:C.
【分析】要求实际面积,必须知道实际的高和实际的底分别是多少,根据比例尺是1:500,列式解答即可.
二、判断题
5.【答案】错误
【解析】【解答】面积相同的两个梯形,形状可能相同,可能不同,原题说法错误.
故答案为:错误.
【分析】因为梯形的面积S=(a+b)×h÷2,即梯形的面积只与上底、下底和高的长度有关,而与梯形的形状无关,据此判断.
6.【答案】错误
【解析】【解答】例如,底是4厘米,高是5厘米,面积:4×5=20(平方厘米);
底是10厘米,高是2厘米,面积:10×2=20(平方厘米),面积相等,但是底和高都不相等,所以原题说法错误.
故答案为:错误
【分析】解答此题要牢记平行四边形面积公式,平行四边形面积=底×高.
7.【答案】 正确
【解析】【解答】解:三角形面积=底×高÷2,所以三角形面积÷高=底÷2(一定),三角形面积和高成正比例。原题说法正确。
故答案为:正确。
【分析】根据三角形面积公式确定三角形面积和高的比值一定还是乘积一定,如果比值一定就成正比例,如果乘积一定就成反比例。
8.【答案】正确
【解析】【分析】梯形当它的上底为0时就转化为三角形,由梯形面积公示和三角形面积公示可知,梯形上下的和与三角形的底相等时,它们的面积相等,高一定相等。
三、填空题
9.【答案】面积;底;高;底;高;S=ah
【解析】【解答】根据平行四边形面积公式的推导过程可知,任意一个平行四边形可以转化成一个面积相等的长方形,这个长方形的长与平行四边形的底相等,宽与平行四边形的高相等,所以平行四边形的面积=底×高,用字母表示为S=ah.
故答案为:面积;底;高;底;高;S=ah.
【分析】把平行四边形沿着一条高切成两个图形,然后把两个图形的斜边拼在一起就成了一个长方形,根据长方形的面积公式推导平行四边形的面积公式.
10.【答案】240
【解析】【解答】解:题目中是两个完全一样的梯形拼成的平行四边形,所以,每个梯形的面积是24×20÷2=240cm2。
故答案为:240。
【分析】两个完全一样的梯形可以拼成一个平行四边形,那么每个梯形的面积是这个平行四边形面积的一半;平行四边形的面积=底×高。
11.【答案】 C;A
【解析】【解答】 把一个平行四边形木条框架拉成长方形,周长不变,面积变大。
故答案为:C;A。
【分析】把一个平行四边形木条框架拉成长方形,形状发生变化,但是木条长度不变,周长不变;由平行四边形变成长方形,底变成长,高变成宽,面积变大,据此解答。
12.【答案】3600;450
【解析】【解答】面积:
160×45÷2
=7200÷2
=3600(平方米)
果树棵数:3600÷8=450(棵)
故答案为:3600;450
【分析】梯形面积=(上底+下底)×高÷2,根据梯形面积公式求出梯形面积,用梯形面积除以8求出果树的棵数即可.
13.【答案】 75平方厘米
【解析】【解答】解:15×10÷2=75(平方厘米)
故答案为:75平方厘米
【分析】本题考查的主要内容是三角形的面积计算问题,根据三角形的面积=底×高÷2进行分析即可.
四、解答题
14.【答案】 解:(5×4+5×1.4÷2-2×1.5)×160
= ×160
=20.5×160
=3280(块)
答:一共用砖3280块。
【解析】【分析】用下面长方形墙的面积加上上面三角形的面积,再减去窗户的面积即可求出这面墙的总面积,用总面积乘平均每平方米用砖的块数求出一共用砖的块数。
15.【答案】(1)解:画高如图:
底是3.4 cm,高是1.9 cm;
面积:3.4×1.9=6.46(cm2)
(2)解:如图:
底是3.8 cm,高是2.0 cm;
面积:3.8×2.0÷2=3.8(cm2)
(3)解:如图:
上底是2.4 cm,下底是4.3 cm,高是2.4 cm;
面积:(2.4+4.3)×2.4÷2
=6.7×2.4÷2
=8.04(cm2)
【解析】【分析】平行四边形面积=底×高,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,先画出图形的高,测量出需要计算的数据后按照公式计算即可。
五、综合题
16.【答案】 (1)1800
(2)4140
【解析】【解答】解:(1)(40×18)÷(0.8×0.5)=1800(棵)
(2)1800×2.3=4140(元)
故答案为:(1)1800;(2)4140.
【分析】(1)先求出每株月季花所占面积,再求出花坛的面积,用花坛面积除每株月季的面积,就可求出这个花坛能栽月季的棵数。
(2)用(1)中月季的棵数乘每株的单价,可以求出一共需要的钱数。
六、应用题
17.【答案】解:①3.14×82× ﹣3.14× × ,
=200.96× ﹣50.24× ,
=50.24﹣25.12,
=25.12(平方厘米);
答:阴影部分的面积为25.12平方厘米;
②3.14×22× +(2×2﹣3.14×22× )
=3.14×3+(4﹣3.14),
=9.42+0.86,
=10.28(平方厘米);
答:阴影部分的面积为10.28平方厘米
【解析】【分析】①阴影部分的面积等于以8厘米为半径的 圆的面积减去以8厘米为直径的半圆的面积,根据圆的面积公式列式解答即可得到答案;②阴影部分的面积等于以2厘米为半径的 圆的面积加上正方形的面积减去以2厘米为半径的 圆的面积的差,根据圆的面积公式和正方形的面积公式列式解答即可得到答案.此题主要考查的是圆的面积公式S=πr2和正方形的面积公式边长×边长的应用.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级上册数学单元测试-6.多边形的面积
一、单选题
1.下面三幅图中,正方形一样大,则三个阴影部分的面积(??? )
A.?一样大??????????????????????B.?第一幅图最大??????????????????????C.?第二幅图最大??????????????????????D.?第三幅图最大
2.如图平行四边形中有A、B、C三个三角形(阴影部分),关于这三个三角形面积之间的关系,下面关系式正确的是( ??)。
A.?A>B+C???????????????????????????????????B.?A=B+C???????????????????????????????????C.?A<B+C
3.如图,AD=DC,AE=EB.若阴影部分的面积是20,则三角形ABC的面积是(? ??)cm2 .
A.?40????????????????????????????????????????B.?60????????????????????????????????????????C.?80????????????????????????????????????????D.?100
4.把一块三角形的地画在比例尺是1:500的图纸上,量得图上三角形的底是12厘米,高8厘米,这块地实际面积是( )
A.?480平方米???????????????????????????????B.?240平方米???????????????????????????????C.?1200平方米
二、判断题
5.面积相同的两个梯形,形状完全相同。
6.判断对错.
如果两个平行四边形的面积相等,那么它们的底和高也一定相等.
7.三角形的底一定,它的面积和高成正比例.(?? )
8.梯形上下底的和与三角形的底相等时,它们的面积相等,高一定相等
三、填空题
9.任意一个平行四边形可以转化成一个________相等的长方形,这个长方形的长与平行四边形的________相等,宽与平行四边形的________相等,所以平行四边形的面积=________×________,用字母表示为________。
10.两个完全一样的梯形拼成一个平行四边形,这个平行四边形的底为24cm,高为20cm。每个梯形的面积是________cm2。
11.把一个平行四边形木条框架拉成长方形,周长________,面积________。
A.变大????????? ?B.变小 ?????????C.不变
12.一个梯形果园的上底与下底的和是160米,高是45米,这个果园的面积是________平方米.如果按每8平方米种一棵果树计算,这个果园一共可以种果树________棵.
13.三角形的面积是________
四、解答题
14.下面是一面墙,中间有一个长2米、宽1.5米的窗户,如果砌这面墙,平均每平方米用砖160块,一共用砖多少块?
15.画一画,量一量,算一算下列图形的面积。(测量精确到毫米。)
(1)
(2)
(3)
五、综合题
16.一个近似平行四边形的花坛,底是40米,高18米。在这个花坛里按株距是0.8米、行距是0.5米栽月季花。
(1)这个花坛能栽月季花________棵.
(2)购买月季花每株需要2.3元,一共需要________元。
六、应用题
17.求图中阴影部分的面积(单位:厘米)
参考答案
一、单选题
1.【答案】 A
【解析】【解答】假设正方形的边长是4,
第一个图形:
4×4-3.14×(4÷2)?
=16-3.14×4
=16-12.56
=3.44
第二个图形:
4×4-3.14×(4÷4)?×4
=16-3.14×4
=16-12.56
=3.44
第三个图形:
4×4-3.14×4?÷4
=16-3.14×4
=16-12.56
=3.44
所以三个阴影部分的面积一样大.
故答案为:A
【分析】三个阴影部分的面积都是正方形面积减去内部空白部分的面积,假设出正方形的边长,然后根据正方形和圆面积公式分别计算阴影部分的面积并作出判断即可.
2.【答案】 B
【解析】【解答】解:A+D=B+C+D,所以A=B+C
故答案为:B
【分析】A和D组成的三角形与B、C、D组成的三角形都是平行四边形面积的一半,因此面积和相等,这样就能判断A、B、C三部分之间的关系。
3.【答案】 C
【解析】【解答】解:如图,AD=DC,AE=EB.若阴影部分的面积是20,则三角形ABC的面积是80cm2。
故答案为:C。
【分析】根据三角形的面积公式,三角形ADE的面积=三角形CDE的面积=20cm2 , 三角形ACE的面积=三角形BCE的面积=40cm2 , 所以三角形ABC的面积是80cm2。
4.【答案】C
【解析】【解答】解:设实际的底是x厘米,实际的高是y厘米,
1:500=12:x
x=500×12
x=6000;
1:500=8:y
y=8×500
y=4000;
实际面积:6000×4000× =12000000(平分厘米);
12000000平分厘米=1200平方米;
答:这块地的实际面积是1200平方米.
故选:C.
【分析】要求实际面积,必须知道实际的高和实际的底分别是多少,根据比例尺是1:500,列式解答即可.
二、判断题
5.【答案】错误
【解析】【解答】面积相同的两个梯形,形状可能相同,可能不同,原题说法错误.
故答案为:错误.
【分析】因为梯形的面积S=(a+b)×h÷2,即梯形的面积只与上底、下底和高的长度有关,而与梯形的形状无关,据此判断.
6.【答案】错误
【解析】【解答】例如,底是4厘米,高是5厘米,面积:4×5=20(平方厘米);
底是10厘米,高是2厘米,面积:10×2=20(平方厘米),面积相等,但是底和高都不相等,所以原题说法错误.
故答案为:错误
【分析】解答此题要牢记平行四边形面积公式,平行四边形面积=底×高.
7.【答案】 正确
【解析】【解答】解:三角形面积=底×高÷2,所以三角形面积÷高=底÷2(一定),三角形面积和高成正比例。原题说法正确。
故答案为:正确。
【分析】根据三角形面积公式确定三角形面积和高的比值一定还是乘积一定,如果比值一定就成正比例,如果乘积一定就成反比例。
8.【答案】正确
【解析】【分析】梯形当它的上底为0时就转化为三角形,由梯形面积公示和三角形面积公示可知,梯形上下的和与三角形的底相等时,它们的面积相等,高一定相等。
三、填空题
9.【答案】面积;底;高;底;高;S=ah
【解析】【解答】根据平行四边形面积公式的推导过程可知,任意一个平行四边形可以转化成一个面积相等的长方形,这个长方形的长与平行四边形的底相等,宽与平行四边形的高相等,所以平行四边形的面积=底×高,用字母表示为S=ah.
故答案为:面积;底;高;底;高;S=ah.
【分析】把平行四边形沿着一条高切成两个图形,然后把两个图形的斜边拼在一起就成了一个长方形,根据长方形的面积公式推导平行四边形的面积公式.
10.【答案】240
【解析】【解答】解:题目中是两个完全一样的梯形拼成的平行四边形,所以,每个梯形的面积是24×20÷2=240cm2。
故答案为:240。
【分析】两个完全一样的梯形可以拼成一个平行四边形,那么每个梯形的面积是这个平行四边形面积的一半;平行四边形的面积=底×高。
11.【答案】 C;A
【解析】【解答】 把一个平行四边形木条框架拉成长方形,周长不变,面积变大。
故答案为:C;A。
【分析】把一个平行四边形木条框架拉成长方形,形状发生变化,但是木条长度不变,周长不变;由平行四边形变成长方形,底变成长,高变成宽,面积变大,据此解答。
12.【答案】3600;450
【解析】【解答】面积:
160×45÷2
=7200÷2
=3600(平方米)
果树棵数:3600÷8=450(棵)
故答案为:3600;450
【分析】梯形面积=(上底+下底)×高÷2,根据梯形面积公式求出梯形面积,用梯形面积除以8求出果树的棵数即可.
13.【答案】 75平方厘米
【解析】【解答】解:15×10÷2=75(平方厘米)
故答案为:75平方厘米
【分析】本题考查的主要内容是三角形的面积计算问题,根据三角形的面积=底×高÷2进行分析即可.
四、解答题
14.【答案】 解:(5×4+5×1.4÷2-2×1.5)×160
= ×160
=20.5×160
=3280(块)
答:一共用砖3280块。
【解析】【分析】用下面长方形墙的面积加上上面三角形的面积,再减去窗户的面积即可求出这面墙的总面积,用总面积乘平均每平方米用砖的块数求出一共用砖的块数。
15.【答案】(1)解:画高如图:
底是3.4 cm,高是1.9 cm;
面积:3.4×1.9=6.46(cm2)
(2)解:如图:
底是3.8 cm,高是2.0 cm;
面积:3.8×2.0÷2=3.8(cm2)
(3)解:如图:
上底是2.4 cm,下底是4.3 cm,高是2.4 cm;
面积:(2.4+4.3)×2.4÷2
=6.7×2.4÷2
=8.04(cm2)
【解析】【分析】平行四边形面积=底×高,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,先画出图形的高,测量出需要计算的数据后按照公式计算即可。
五、综合题
16.【答案】 (1)1800
(2)4140
【解析】【解答】解:(1)(40×18)÷(0.8×0.5)=1800(棵)
(2)1800×2.3=4140(元)
故答案为:(1)1800;(2)4140.
【分析】(1)先求出每株月季花所占面积,再求出花坛的面积,用花坛面积除每株月季的面积,就可求出这个花坛能栽月季的棵数。
(2)用(1)中月季的棵数乘每株的单价,可以求出一共需要的钱数。
六、应用题
17.【答案】解:①3.14×82× ﹣3.14× × ,
=200.96× ﹣50.24× ,
=50.24﹣25.12,
=25.12(平方厘米);
答:阴影部分的面积为25.12平方厘米;
②3.14×22× +(2×2﹣3.14×22× )
=3.14×3+(4﹣3.14),
=9.42+0.86,
=10.28(平方厘米);
答:阴影部分的面积为10.28平方厘米
【解析】【分析】①阴影部分的面积等于以8厘米为半径的 圆的面积减去以8厘米为直径的半圆的面积,根据圆的面积公式列式解答即可得到答案;②阴影部分的面积等于以2厘米为半径的 圆的面积加上正方形的面积减去以2厘米为半径的 圆的面积的差,根据圆的面积公式和正方形的面积公式列式解答即可得到答案.此题主要考查的是圆的面积公式S=πr2和正方形的面积公式边长×边长的应用.
