2020年春人教版数学八年级下册同步习题:17.1 勾股定理(解析版)
文档属性
| 名称 | 2020年春人教版数学八年级下册同步习题:17.1 勾股定理(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 404.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-17 00:00:00 | ||
图片预览


文档简介
2020年春人教版八年级下册同步习题:17.1 勾股定理
一.选择题(共10小题)
1.如图,AB=AC,则数轴上点C所表示的数为( )
A.+1 B.﹣1 C.﹣+1 D.﹣﹣1
2.如图,在边长为1个单位长度的小正方形网格中,点A、B都是格点(即网格线的交点),则线段AB的长度为( )
A.3 B.5 C.6 D.4
3.直角三角形两条直角边的长分别为3和4,则斜边长为( )
A.4 B.5 C.6 D.10
4.等腰三角形腰长为13,底边长为10,则它底边上的高为( )
A.12 B.7 C.5 D.6
5.若一直角三角形两边长为4和5,则第三边长为( )
A.3 B. C.3或 D.不确定
6.一直角三角形的三边分别为2、3、x,那么x为( )
A. B. C.或 D.无法确定
7.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,已知正方形A、B、C的面积依次为2、4、3,则正方形D的面积为( )
A.8 B.9 C.27 D.45
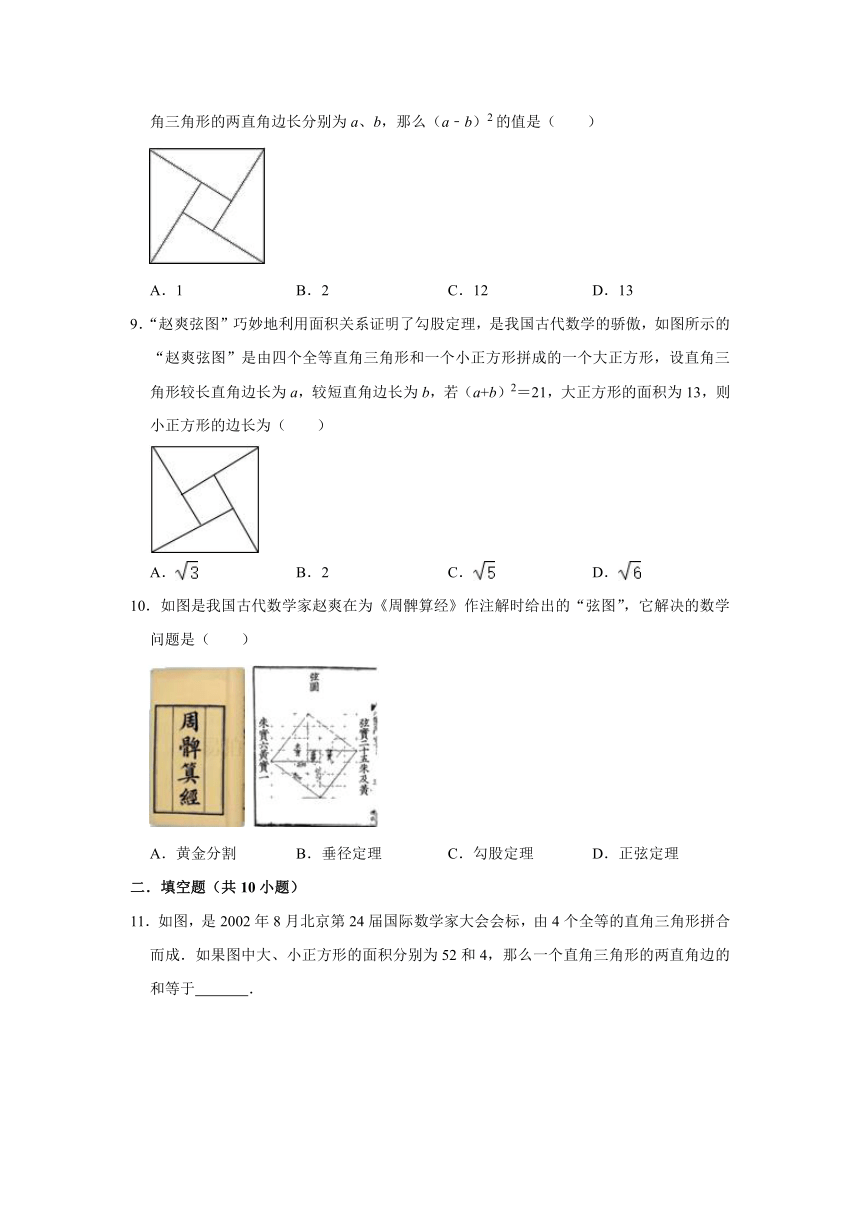
8.我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a、b,那么(a﹣b)2的值是( )
A.1 B.2 C.12 D.13
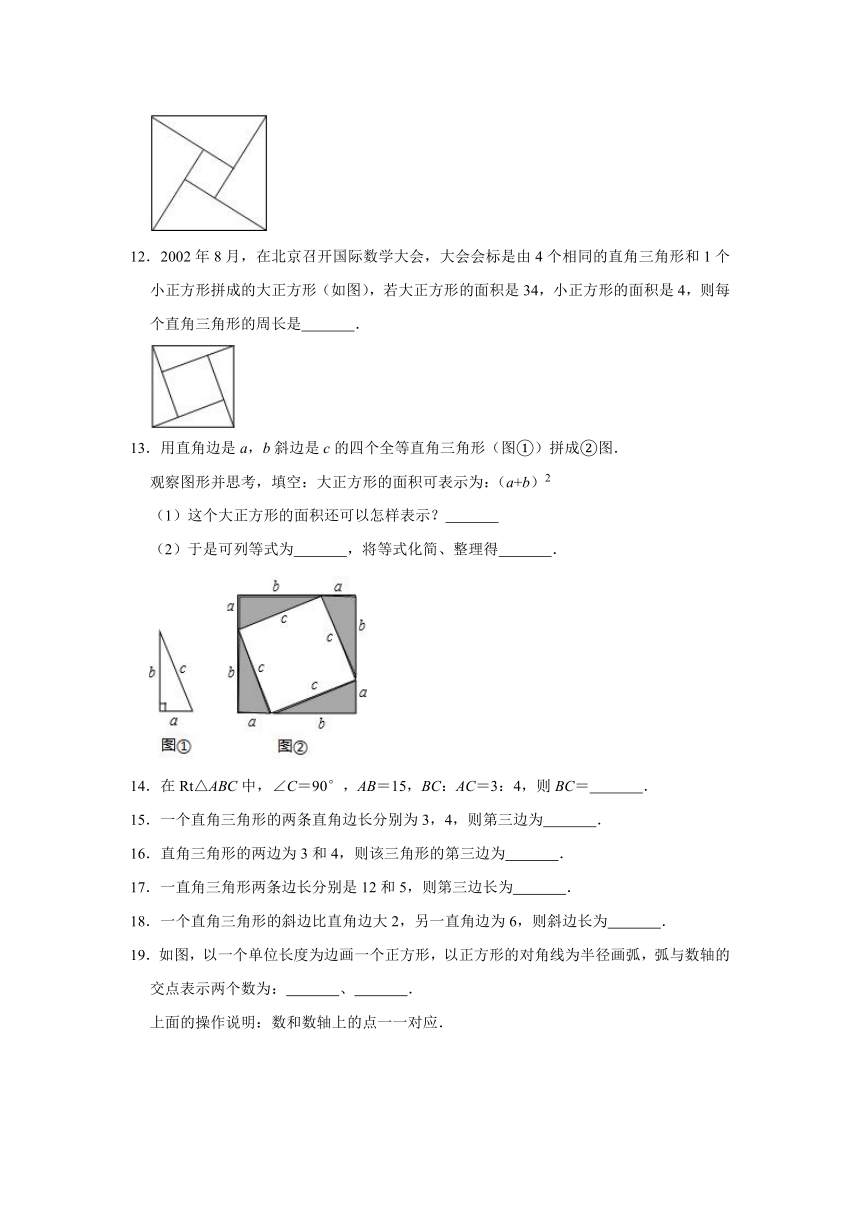
9.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的边长为( )
A. B.2 C. D.
10.如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是( )
A.黄金分割 B.垂径定理 C.勾股定理 D.正弦定理
二.填空题(共10小题)
11.如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的和等于 .
12.2002年8月,在北京召开国际数学大会,大会会标是由4个相同的直角三角形和1个小正方形拼成的大正方形(如图),若大正方形的面积是34,小正方形的面积是4,则每个直角三角形的周长是 .
13.用直角边是a,b斜边是c的四个全等直角三角形(图①)拼成②图.
观察图形并思考,填空:大正方形的面积可表示为:(a+b)2
(1)这个大正方形的面积还可以怎样表示?
(2)于是可列等式为 ,将等式化简、整理得 .
14.在Rt△ABC中,∠C=90°,AB=15,BC:AC=3:4,则BC= .
15.一个直角三角形的两条直角边长分别为3,4,则第三边为 .
16.直角三角形的两边为3和4,则该三角形的第三边为 .
17.一直角三角形两条边长分别是12和5,则第三边长为 .
18.一个直角三角形的斜边比直角边大2,另一直角边为6,则斜边长为 .
19.如图,以一个单位长度为边画一个正方形,以正方形的对角线为半径画弧,弧与数轴的交点表示两个数为: 、 .
上面的操作说明:数和数轴上的点一一对应.
20.如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形,若斜边AB=2,则图中阴影部分的面积和为 .
三.解答题(共5小题)
21.如图,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为点N,求证:AN2﹣BN2=AC2.
22.如图,已知在△ABC中,AB=12,AC=10,BC边上的高AD=8,求BC边的长.
23.正方形网格中的每个小正方形边长都是1,
(1)请在图中画出等腰△ABC,使AB=AC=,BC=;
(2)在△ABC中,AB边上的高为 .
24.在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C所对的边.
(1)若b=2,c=3,求a的值;
(2)若a:c=3:5,b=16,求△ABC的面积.
25.如图.大正方形是由4个相等的直角三角形和一个小正方形拼成的.
(1)在左图中,已知AE=3,AF=4,求小正方形的面积;
(2)在右图中,已知AE=a,AF=b,求大正方形的面积.
参考答案与试题解析
一.选择题(共10小题)
1.如图,AB=AC,则数轴上点C所表示的数为( )
A.+1 B.﹣1 C.﹣+1 D.﹣﹣1
【分析】根据勾股定理列式求出AB的长,即为AC的长,再根据数轴上的点的表示解答.
【解答】解:由勾股定理得,AB==,
∴AC=,
∵点A表示的数是﹣1,
∴点C表示的数是﹣1.
故选:B.
2.如图,在边长为1个单位长度的小正方形网格中,点A、B都是格点(即网格线的交点),则线段AB的长度为( )
A.3 B.5 C.6 D.4
【分析】由勾股定理即可得出线段AB的长.
【解答】解:由勾股定理得:AB==5;
故选:B.
3.直角三角形两条直角边的长分别为3和4,则斜边长为( )
A.4 B.5 C.6 D.10
【分析】利用勾股定理即可求出斜边长.
【解答】解:由勾股定理得:斜边长为:=5.
故选:B.
4.等腰三角形腰长为13,底边长为10,则它底边上的高为( )
A.12 B.7 C.5 D.6
【分析】在等腰三角形的腰和底边高线所构成的直角三角形中,根据勾股定理即可求得底边上高线的长度.
【解答】解:如图:
∵△ABC中,AB=AC,AD⊥BC;
∴BD=DC=BC=5;
Rt△ABD中,AB=13,BD=5;
由勾股定理,得:AD===12.
故选:A.
5.若一直角三角形两边长为4和5,则第三边长为( )
A.3 B. C.3或 D.不确定
【分析】由于直角三角形的斜边不能确定,故应分5是直角边或5是斜边两种情况进行讨论.
【解答】解:当5是直角边时,则第三边==;
当5是斜边时,则第三边==3.
综上所述,第三边的长是或3.
故选:C.
6.一直角三角形的三边分别为2、3、x,那么x为( )
A. B. C.或 D.无法确定
【分析】分x为斜边与直角边两种情况求出x的值即可.
【解答】解:当x为斜边时,x==;
当x为直角边时,x==.
故选:C.
7.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,已知正方形A、B、C的面积依次为2、4、3,则正方形D的面积为( )
A.8 B.9 C.27 D.45
【分析】设正方形D的面积为x,根据图形得出方程2+4=x﹣3,求出即可.
【解答】解:设正方形D的面积为x,
∵正方形A、B、C的面积依次为2、4、3,
∴根据图形得:2+4=x﹣3,
解得:x=9,
故选:B.
8.我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a、b,那么(a﹣b)2的值是( )
A.1 B.2 C.12 D.13
【分析】根据勾股定理可以求得a2+b2等于大正方形的面积,然后求四个直角三角形的面积,即可得到ab的值,然后根据(a﹣b)2=a2﹣2ab+b2即可求解.
【解答】解:根据勾股定理可得a2+b2=13,
四个直角三角形的面积是:ab×4=13﹣1=12,即:2ab=12
则(a﹣b)2=a2﹣2ab+b2=13﹣12=1.
故选:A.
9.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的边长为( )
A. B.2 C. D.
【分析】观察图形可知,小正方形的面积=大正方形的面积﹣4个直角三角形的面积,利用已知(a+b)2=21,大正方形的面积为13,可以得出直角三角形的面积,进而求出答案.
【解答】解:如图所示:
∵(a+b)2=21,
∴a2+2ab+b2=21,
∵大正方形的面积为13,
2ab=21﹣13=8,
∴小正方形的面积为13﹣8=5.
故小正方形的边长为,
故选:C.
10.如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是( )
A.黄金分割 B.垂径定理 C.勾股定理 D.正弦定理
【分析】“弦图”,说明了直角三角形的三边之间的关系,解决了勾股定理的证明.
【解答】解:“弦图”,说明了直角三角形的三边之间的关系,解决的问题是:勾股定理.
故选:C.
二.填空题(共10小题)
11.如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的和等于 10 .
【分析】设两直角边分别为x,y,根据勾股定理求出大正方形的面积和小正方形的面积,列出方程组,解方程组求出两直角边长的和.
【解答】解:设设三角形的两直角边分别为x,y,
则,
由②得x2+y2﹣2xy=4…③,
①﹣③得2xy=48
则(x+y)2=x2+y2+2xy=52+48=100,
x+y==10.
故答案是:10.
12.2002年8月,在北京召开国际数学大会,大会会标是由4个相同的直角三角形和1个小正方形拼成的大正方形(如图),若大正方形的面积是34,小正方形的面积是4,则每个直角三角形的周长是 .
【分析】设直角三角形的三边分别是a、b、c,根据正方形的面积公式即可求得c2=34,(b﹣a)2=4,然后根据勾股定理,求得a+b+c的值即可.
【解答】解:设直角三角形的三边分别是a、b、c,如图.
∵大正方形的面积是34,小正方形的面积是4,
∴c2=34,(b﹣a)2=4,
即c=,a2+b2﹣2ab=4,
又∵a2+b2=c2,
∴ab=15.
∴(a+b)2=a2+b2+2ab=34+2×15=64,
∴a+b=8,
∴a+b+c=8+.
故答案是:8+.
13.用直角边是a,b斜边是c的四个全等直角三角形(图①)拼成②图.
观察图形并思考,填空:大正方形的面积可表示为:(a+b)2
(1)这个大正方形的面积还可以怎样表示? c2+2ab
(2)于是可列等式为 (a+b)2=c2+2ab ,将等式化简、整理得 a2+b2=c2 .
【分析】(1)大正方形的面积=小正方形的面积+4个直角三角形的面积;
(2)根据大正方形的面积不变列出等式并整理.
【解答】解:(1)依题意得:大正方形的面积可表示为:c2+4×ab=c2+2ab.
故答案是:c2+2ab.
(2)依题意得:(a+b)2=c2+2ab.
整理得:a2+b2=c2.
故答案是:(a+b)2=c2+2ab.a2+b2=c2.
14.在Rt△ABC中,∠C=90°,AB=15,BC:AC=3:4,则BC= 9 .
【分析】设BC=3x,AC=4x,又其斜边AB=15,再根据勾股定理即可得出答案.
【解答】解:设BC=3x,AC=4x,又其斜边AB=15,
∴9x2+16x2=152,
解得:x=3或﹣3(舍去),∴BC=3x=9.
故答案为:9.
15.一个直角三角形的两条直角边长分别为3,4,则第三边为 5 .
【分析】根据勾股定理计算即可.
【解答】解:由勾股定理得:第三边为:=5,
故答案为:5.
16.直角三角形的两边为3和4,则该三角形的第三边为 5或 .
【分析】本题已知直角三角形的两边长,但未明确这两条边是直角边还是斜边,因此两条边中的较长边4既可以是直角边,也可以是斜边,所以求第三边的长必须分类讨论,即4是斜边或直角边的两种情况,然后利用勾股定理求解.
【解答】解:设第三边为x,
(1)若4是直角边,则第三边x是斜边,由勾股定理得:
32+42=x2,所以x=5;
(2)若4是斜边,则第三边x为直角边,由勾股定理得:
32+x2=42,所以x=;
所以第三边的长为5或.
故答案为:5或.
17.一直角三角形两条边长分别是12和5,则第三边长为 13或 .
【分析】只给出了两条边而没有指明是直角边还是斜边,所以应该分两种情况进行分析.一种是两边均为直角边;另一种是较长的边是斜边,根据勾股定理可求得第三边.
【解答】解:①12和5均为直角边,则第三边为=13.
②12为斜边,5为直角边,则第三边为=.
故答案为:13或.
18.一个直角三角形的斜边比直角边大2,另一直角边为6,则斜边长为 10 .
【分析】设斜边为x,根据勾股定理列方程即可解答.
【解答】解:设斜边为x,
则x2=(x﹣2)2+62解得x=10.
19.如图,以一个单位长度为边画一个正方形,以正方形的对角线为半径画弧,弧与数轴的交点表示两个数为: 1﹣ 、 1+ .
上面的操作说明:数和数轴上的点一一对应.
【分析】根据题意知,DO=OA=OB,所以在正方形中利用勾股定理求得对角线OD的长度,再结合图形根据数轴上的点与实数的对应关系即可求解.
【解答】解:∵DO2=12+12=2,
∴DO=,
∵点A在1左边,点B在1右边.
∴点A表示的实数是1﹣,点B表示的实数是1+;
故答案是:1﹣,1+.
20.如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形,若斜边AB=2,则图中阴影部分的面积和为 2 .
【分析】根据勾股定理和等腰直角三角形的面积公式,可以证明:以直角三角形的两条直角边为斜边的等腰直角三角形的面积和等于以斜边为斜边的等腰直角三角形的面积.则阴影部分的面积即为以斜边为斜边的等腰直角三角形的面积的2倍.
【解答】解:设两条直角边是a,b,则a2+b2=22,
则S阴影=(a)2+(b)2+×()2=×(a2+b2)+1=×4+1=2,
故答案为:2.
三.解答题(共5小题)
21.如图,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为点N,求证:AN2﹣BN2=AC2.
【分析】在直角三角形BNM和ANM中利用勾股定理可以得到BN2=BM2﹣MN2,AN2=AM2﹣MN2,然后得到BN2﹣AN2=(BM2﹣MN2)﹣(AM2﹣MN2)=BM2﹣AM2;又在直角三角形AMC中,AM2=AC2+CM2,代入前面的式子中即可得出结论.
【解答】证明:∵MN⊥AB于N,
∴BN2=BM2﹣MN2,AN2=AM2﹣MN2
∴BN2﹣AN2=BM2﹣AM2,
又∵∠C=90°,
∴AM2=AC2+CM2
∴BN2﹣AN2=BM2﹣AC2﹣CM2,
又∵BM=CM,
∴BN2﹣AN2=﹣AC2,
即AN2﹣BN2=AC2.
22.如图,已知在△ABC中,AB=12,AC=10,BC边上的高AD=8,求BC边的长.
【分析】如图,运用勾股定理直接求出BD、CD的长度,即可解决问题.
【解答】解:如图,∵AD⊥BC,
∴BD2=122﹣82,CD2=102﹣82,
∴BD=,CD=6,
∴BC=6+.
23.正方形网格中的每个小正方形边长都是1,
(1)请在图中画出等腰△ABC,使AB=AC=,BC=;
(2)在△ABC中,AB边上的高为 .
【分析】(1)利用数形结合的思想解决问题即可;
(2)利用三角形的面积,构建方程求解即可;
【解答】解:(1)△ABC如图所示.
(2)设CD⊥AB,
∵S△ABC=?AB?CD=4﹣×2×1﹣×2×1﹣×1×1,
∴CD=,
故答案为.
24.在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C所对的边.
(1)若b=2,c=3,求a的值;
(2)若a:c=3:5,b=16,求△ABC的面积.
【分析】(1)利用勾股定理直接计算即可;
(2)设a=3x,c=5x,由勾股定理可求出x的值,进而可求出求△ABC的面积.
【解答】解:
(1)∵△ABC中,∠C=90°,b=2,c=3,
∴a==;
(2)∵a:c=3:5,
∴设a=3x,c=5x,
∵b=16,
∴9x2+162=25x2,
解得:x=4,
∴a=12,
∴△ABC的面积=×12×16=96.
25.如图.大正方形是由4个相等的直角三角形和一个小正方形拼成的.
(1)在左图中,已知AE=3,AF=4,求小正方形的面积;
(2)在右图中,已知AE=a,AF=b,求大正方形的面积.
【分析】(1)在直角△AEF中利用勾股定理求得EF2,则小正方形的面积等于EF2,据此即可求解;
(2)在直角△AEF中利用勾股定理求得EF2,则大正方形的面积等于EF2,据此即可求解.
【解答】解:(1)在直角△AEF中,EF2=AE2+AF2=32+42=25,则小正方形的面积是25;
(2)在直角△AEF中,EF2=AE2+AF2=a2+b2,则大正方形的面积是a2+b2.
