北师大版七年级数学下册同步精练专题 4.3探索三角形全等的条件同步训练(含解析)
文档属性
| 名称 | 北师大版七年级数学下册同步精练专题 4.3探索三角形全等的条件同步训练(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 194.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-17 00:00:00 | ||
图片预览



文档简介
4.3探索三角形全等的条件同步训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
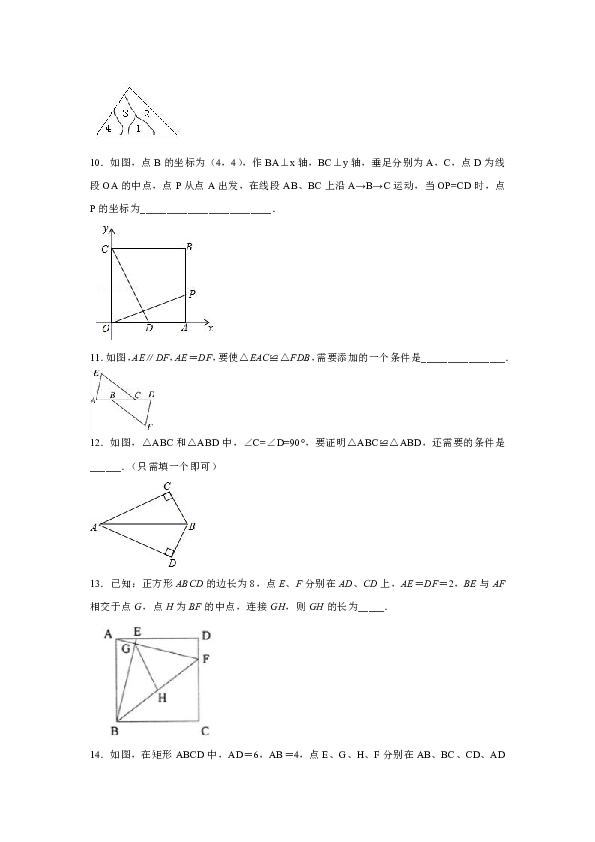
1.如图,已知AB=CD,BC=AD,∠B=23°,则∠D为( )
A.67° B.23° C.46° D.无法确定
2.已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )
A.AE=AC B.∠B=∠D C.BC=DE D.∠C=∠E
3.我国的纸伞工艺十分巧妙,如图,伞圈 D 能沿着伞柄滑动,伞不论张开还是缩拢,伞柄 AP 始终平分同一平面内所成的角∠BAC,为了证明这个结论,我们的依据是
A.SAS B.SSS C.AAS D.ASA
4.如图,已知BD是∠ABE的角平分线,增加哪一条件不能证明△ABD≌△EBD( )
A.AD=ED B.AB=EB C.DB平分∠ADE D.∠A=∠BED
5.如图,已知∠CAB=∠DBA,则添加一个条件,不一定能使△ABC≌△BAD的是( )
A.AC=BD B.∠C=∠D
C.BC=AD D.∠CBD=∠DAC
6.在△ABC和△DEF中,已知AB=DE,∠A=∠D,若补充下列条件中的任意一条,就能判定△ABC≌△DEF的是 ( )
①AC=DF ②BC=EF ③∠B=∠E ④∠C=∠F
A.①②③ B.②③④
C.①③④ D.①②④
7.已知在△ABC和△DEF中,∠A=∠D=90°,则下列条件中不能判定△ABC和△DEF全等的是( )
A.AB=DE,AC=DF B.AC=EF,BC=DF C.AB=DE,BC=EF D.∠C=∠F,BC=EF
8.如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF,下列结论中正确结论的个数是 ( )
①△ABG≌△AFG;②∠EAG=450;③BG=GC; ④AG∥CF; ⑤S△FGC=3.6
A.2个 B.3个 C.4个 D.5个
二、填空题
9.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块)你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带______.依据______
10.如图,点B的坐标为(4,4),作BA⊥x轴,BC⊥y轴,垂足分别为A,C,点D为线段OA的中点,点P从点A出发,在线段AB、BC上沿A→B→C运动,当OP=CD时,点P的坐标为_________________________.
11.如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加的一个条件是________________.
12.如图,△ABC和△ABD中,∠C=∠D=90°,要证明△ABC≌△ABD,还需要的条件是______.(只需填一个即可)
13.已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.
14.如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于________.
三、解答题
15.如图,点分别是对角线上两点,.求证:.
16.已知:如图,在△ABC中,O是边BC的中点,E是线段AB延长线上一点,过点C作CD∥BE,交线段EO的延长线于点D,连接BD,CE.
(1)求证:CD=BE;
(2)如果∠ABD=2∠BED,求证:四边形BECD是菱形.
17.如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:BC=DE
(2)若∠A=40°,求∠BCD的度数.
18.(本题满分10分)如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.
求证:(1)求证:△ABE≌△ACD;
(2)求证:四边形BCDE是矩形.
参考答案
1.B
【解析】
试题解析:连接AC,
∵AB=CD,BC=AD(已知),
AC=AC,
∴△ABC≌△ACD,
故选B.
2.C
【解析】
【分析】
根据∠1=∠2可利用等式的性质得到∠BAC=∠DAE,然后再根据所给的条件利用全等三角形的判定定理进行分析即可.
【详解】
解:∵∠1=∠2, ∴∠1+∠DAC=∠2+∠DAC, ∴∠BAC=∠DAE, A、添加AE=AC,可利用SAS定理判定△ABC≌△ADE,故此选项不合题意; B、添加∠B=∠D,可利用SAS定理判定△ABC≌△ADE,故此选项不合题意; C、添加BC=DE,不能判定△ABC≌△ADE,故此选项符合题意; D、添加∠C=∠E,可利用AAS定理判定△ABC≌△ADE,故此选项不合题意; 故选C.
【点睛】
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
3.B
【解析】
【分析】
根据确定三角形全等的条件进行判定即可得解.
【详解】
解:根据伞的结构,AE=AF,伞骨DE=DF,AD是公共边, ∵在△ADE和△ADF中,
∴△ADE≌△ADF(SSS), ∴∠DAE=∠DAF, 即AP平分∠BAC. 故选:B.
【点睛】
本题考查了全等三角形的应用,理解题意确定出全等的三角形以及全等的条件是解题的关键.
4.A
【解析】
【分析】
根据全等三角形的判定对各选项进行分析.
【详解】
∵BD是∠ABE的角平分线,
∴∠ABD=∠EBD,且BD是公共边,
A选项:若AD=ED,则SSA,不能判定三角形全等,故符合题意;
B选项:若AB=EB,根据SAS可以判定三角形全等,故不符合题意;
C选项:若DB平分∠ADE,则∠ADB=∠EDB,根据ASA可判定三角形全等,故不符合题意;
D选项:若∠A=∠BED,根据AAS可判定三角形全等,故不符合题意;
故选:A.
【点睛】
考查了全等三角形的判定:判定三角形全等的方法有“SSS”、“AAS”、“SAS”、“ASA”.
5.C
【解析】
∵∠CAB=∠DBA,AB=BA, ∴当AC=BD时,依据SAS能使△ABC≌△BAD;当∠C=∠D时,依据AAS能使△ABC≌△BAD;当∠CBD=∠DAC时,∠ABC=∠BAD,依据ASA能使△ABC≌△BAD;当BC=AD时,不一定能使△ABC≌△BAD;故选:C.
6.C
【解析】
如图,∵AB=DE,∠A=∠D,
∴根据“边角边”可添加AC=DF,
根据“角边角”可添加∠B=∠E,
根据“角角边”可添加∠C=∠F.
所以补充①③④可判定△ABC≌△DEF.
故选C.
7.B
【解析】
【分析】
根据全等三角形的判定,逐个分析即可.
【详解】
A. AB=DE,AC=DF, 且∠A=∠D=90°,根据SAS,△ABC和△DEF全等;
B. AC=EF,BC=DF , 且∠A=∠D=90°,不能判定△ABC和△DEF全等;
C. AB=DE,BC=EF ,且∠A=∠D=90°,根据HL,△ABC和△DEF全等;
D. ∠C=∠F,BC=EF, 且∠A=∠D=90°,根据AAS,△ABC和△DEF全等.
故选B
【点睛】
本题考核知识点:全等三角形的判定. 解题关键点:熟记全等三角形的判定.
8.D
【解析】
分析:①用HL证明△ABG≌△AFG;②由△ADE≌△AFE,△ABG≌△AFG,得到∠EAG=∠BAD;③在直角三角形CEG中,由勾股定理求GC的长;④根据基本图形“等腰三角形+角平分线→平行线”证明;⑤由GF:EG=3:5,得S△FCG:S△ECG=3:5.
详解:①根据轴对称的性质得,△ADE≌△AFE,
所以AD=AF,∠AFE=∠D=90°.
因为AB=AD,∠B=90°,所以AB=AF,
因为AG=AG,所以△ABG≌△AFG.
则①正确;
②因为△ADE≌△AFE,△ABG≌△AFG,
所以∠DAE=∠FAE,∠BAG=∠FAG,
所以∠EAG=∠FAE+∠FAE=∠BAD=×90°=45°.
则②正确;
③因为△ADE≌△AFE,△ABG≌△AFG,
所以ED=EF,GB=GF,所以EG=DE+BG,
设BG=x,则CG=FG=6-x,DE=2,CE=4,EG=x+2=x+2.
Rt△CEG中,由勾股定理得,CG2+CE2=EG2,
所以(6-x)2+42=(x+2)2,解得x=3.
则CG=6-x=3,又BG=x=3,所以BG=CG.
则③正确;
④因为△ABG≌△AFG,所以∠AGB=∠AGF.
因为BG=CG,BG=GF,所以CG=GF,所以∠GCF=∠GFC.
因为∠BGE=∠GCF+∠GFC,所以∠AGB=∠GCF,所以AG∥CF.
则④正确;
⑤因为GF=3,GE=5,所以S△FGC=S△GCE=×GC·CE=××3×4=3.6.
则⑤正确.
故选D.
点睛:正方形的折叠问题中涉及到线段的长一般用勾股定理列方程求解,要熟悉基本图形“角平分线+平行线→等腰三角形”,把“角平分线”,“平行线”,“等腰三角形”,这三个中的任意两个作为题设,另一个作为结论所得的命题都是真命题.
9.2 角边角
【解析】
【分析】
本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.
【详解】
1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的。
故答案为:2.
【点睛】
考查全等三角形的判定,掌握全等三角形的判定定理是解题的关键.
10.(2,4)或(4,2).
【解析】
试题分析:①当点P在正方形的边AB上时,在Rt△OCD和Rt△OAP中,∵OC=OA,CD=OP,∴Rt△OCD≌Rt△OAP,∴OD=AP,∵点D是OA中点,∴OD=AD=OA,∴AP=AB=2,∴P(4,2);
②当点P在正方形的边BC上时,同①的方法,得出CP=BC=2,∴P(2,4).
综上所述:P(2,4)或(4,2).故答案为(2,4)或(4,2).
考点:全等三角形的判定与性质;坐标与图形性质;分类讨论.
11.AB=CD或∠E=∠F(答案不唯一)
【解析】
分析:添加条件AB=CD可证明AC=BD,然后再根据AE∥FD,可得∠A=∠D,再利用SAS定理证明△EAC≌△FDB即可.
详解:∵AE∥FD,
∴∠A=∠D,
∵AB=CD,
∴AC=BD,
在△AEC和△DFB中,
,
∴△EAC≌△FDB(SAS),
故答案为:AB=CD.
点睛:此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
12.AC=AD
【解析】
【分析】
根据∠C=∠D=90°利用HL定理推出两三角形全等即可.
【详解】
添加的条件是AC=AD,理由是:
∵∠C=∠D=90°,
∴在Rt△ACB和Rt△ADB中
,
∴Rt△ACB≌Rt△ADB(HL).
故答案为AD=AC.
【点睛】
本题考查了全等三角形的判定定理的应用,注意两直角三角形全等的方法有SAS,ASA,AAS,SSS,HL,此题是一道开放性的题目,答案不唯一.
13.5
【解析】
【分析】
根据正方形的四条边都相等可得AB=AD,每一个角都是直角可得∠BAE=∠D=90°;然后利用“边角边”证明△ABE≌△DAF得∠ABE=∠DAF,进一步得∠AGE=∠BGF=90°,从而知GH=BF,利用勾股定理求出BF的长即可得出答案.
【详解】
∵四边形ABCD为正方形, ∴∠BAE=∠D=90°,AB=AD, 在△ABE和△DAF中,∵AB=AD,∠BAE=∠D,AE=DF, ∴△ABE≌△DAF(SAS), ∴∠ABE=∠DAF, ∵∠ABE+∠BEA=90°, ∴∠DAF+∠BEA=90°, ∴∠AGE=∠BGF=90°, ∵点H为BF的中点, ∴GH=BF, ∵BC=8,CF=CD-DF=8-2=6, ∴BF==10, ∴GH=BF=5.
【点睛】
本题考查了正方形的性质,全等三角形的判定与性质,直角三角形两锐角互余等知识,掌握三角形全等的判定方法与正方形的性质是解题的关键.
14.7
【解析】
考点:矩形的性质;平行四边形的判定与性质.
分析:连接EG,FH,根据题目数据可以证明△AEF与△CGH全等,根据全等三角形对应边相等可得EF=GH,同理可得EG=FH,然后根据两组对边相等的四边形是平行四边形可得四边形EGHF是平行四边形,所以△PEF和△PGH的面积和等于平行四边形EGHF的面积的一半,再利用平行四边形EGHF的面积等于矩形ABCD的面积减去四周四个小直角三角形的面积即可求解.
解:∵在矩形ABCD中,AD=6,AB=4,AF=CG=2,BE=DH=1,
∴AE=AB-BE=4-1=3,
CH=CD-DH=4-1=3,
∴AE=CH,
在△AEF与△CGH中,,
∴△AEF≌△CGH(SAS),
∴EF=GH,
同理可得,△BGE≌△DFH,
∴EG=FH,
∴四边形EGHF是平行四边形,
∵△PEF和△PGH的高的和等于点H到直线EF的距离,
∴△PEF和△PGH的面积和=×平行四边形EGHF的面积,
平行四边形EGHF的面积
=4×6-×2×3-×1×(6-2)-×2×3-×1×(6-2),
=24-3-2-3-2,
=14,
∴△PEF和△PGH的面积和=×14=7.
故答案为7.
15.见解析
【解析】
【分析】
用SAS证明△BAF≌△DCE即可说明∠DEC=∠BFA.
【详解】
证明::∵四边形为平行四边形,
∴,
∴,
又,
∴≌,
∴.
【点睛】
本题主要考查了平行四边形的性质、全等三角形的判定和性质,解决这类问题一般是四边形转化为三角形处理.
16.见解析
【解析】
【分析】
(1)可通过全等三角形来证明简单的线段相等,△COD和△BOE中,已知了CO=BO,∠COD=∠BOE,CD∥BE,因此不难得出两三角形全等,进而可得出CD=BE.
(2)需先证明四边形AFCE是平行四边形,那么邻边相等的平行四边形是菱形.
【详解】
(1)∵CD∥BE,
∴∠CDE=∠DEB.
∵O是边BC的中点,
∴CO=BO.
在△COD和△BOE中,
∴△COD≌△BOE(AAS).
∴CD=BE.
(2)∵CD∥BE,CD=BE,
∴四边形BECD是平行四边形.
∵∠ABD=2∠BED,∠ABD=∠BED+∠BDE,
∴∠BED=∠BDE.
∴BD=BE.
∴四边形BECD是菱形.
点睛:本题考查了平行线的性质,平行四边形的判定,菱形的判定,全等三角形的判定与性质,注意掌握两条线段在不同的三角形中要证明相等时,通常是利用全等来进行证明.
17.(1)证明见解析;(2)140°;
【解析】
【分析】
(1)根据平行线的性质可得∠ACB=∠DEC,∠ACD=∠D,再由∠ACD=∠B可得∠D=∠B,然后可利用AAS证明△ABC≌△CDE,进而得到CB=DE; (2)根据全等三角形的性质可得∠A=∠DCE=40°,然后根据邻补角的性质进行计算即可.
【详解】
(1)∵AC∥DE,
∴∠ACB=∠DEC,∠ACD=∠D,
∵∠ACD=∠B.
∴∠D=∠B,
在△ABC和△DEC中,,
∴△ABC≌△CDE(AAS),
∴BC=DE;
(2)∵△ABC≌△CDE,
∴∠A=∠DCE=40°
∴∠BCD=180°–40°=140°.
【点睛】
本题考查的是全等三角形,熟练掌握全等三角形的性质是解题的关键.
18.(1)见解析;(2)见解析
【解析】
试题分析:(1)根据条件∠BAD=∠CAE证出∠EAB=∠DAC即可用SAS证明△ABE≌△ACD;(2)由(1)可得BE=CD,进而可证四边形BCDE为平行四边形,然后再证明∠DCB=90°即可.
试题解析:(1)证明:∵∠BAD=∠CAE ∴∠EAB=∠DAC,在△ABE和△ACD中
∵AB=AC,∠EAB=∠DAC,AE=AD
∴△ABE≌△ACD(SAS)
(2)∵△ABE≌△ACD ∴BE=CD,又DE=BC
∴四边形BCDE为平行四边形.
∵AB=AC,∴∠ABC=∠ACB
∵△ABE≌△ACD∴∠ABE=∠ACD∴∠EBC=∠DCB
∵四边形BCDE为平行四边形∴EB∥DC∴∠EBC+∠DCB=180°
∴∠EBC=∠DCB=90°
四边形BCDE是矩形.
(此题也可连接EC,DB,通过全等,利用对角线相当的平行四边形是矩形进行证明)
考点:1.全等三角形的判定与性质;2.矩形的判定.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知AB=CD,BC=AD,∠B=23°,则∠D为( )
A.67° B.23° C.46° D.无法确定
2.已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )
A.AE=AC B.∠B=∠D C.BC=DE D.∠C=∠E
3.我国的纸伞工艺十分巧妙,如图,伞圈 D 能沿着伞柄滑动,伞不论张开还是缩拢,伞柄 AP 始终平分同一平面内所成的角∠BAC,为了证明这个结论,我们的依据是
A.SAS B.SSS C.AAS D.ASA
4.如图,已知BD是∠ABE的角平分线,增加哪一条件不能证明△ABD≌△EBD( )
A.AD=ED B.AB=EB C.DB平分∠ADE D.∠A=∠BED
5.如图,已知∠CAB=∠DBA,则添加一个条件,不一定能使△ABC≌△BAD的是( )
A.AC=BD B.∠C=∠D
C.BC=AD D.∠CBD=∠DAC
6.在△ABC和△DEF中,已知AB=DE,∠A=∠D,若补充下列条件中的任意一条,就能判定△ABC≌△DEF的是 ( )
①AC=DF ②BC=EF ③∠B=∠E ④∠C=∠F
A.①②③ B.②③④
C.①③④ D.①②④
7.已知在△ABC和△DEF中,∠A=∠D=90°,则下列条件中不能判定△ABC和△DEF全等的是( )
A.AB=DE,AC=DF B.AC=EF,BC=DF C.AB=DE,BC=EF D.∠C=∠F,BC=EF
8.如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF,下列结论中正确结论的个数是 ( )
①△ABG≌△AFG;②∠EAG=450;③BG=GC; ④AG∥CF; ⑤S△FGC=3.6
A.2个 B.3个 C.4个 D.5个
二、填空题
9.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块)你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带______.依据______
10.如图,点B的坐标为(4,4),作BA⊥x轴,BC⊥y轴,垂足分别为A,C,点D为线段OA的中点,点P从点A出发,在线段AB、BC上沿A→B→C运动,当OP=CD时,点P的坐标为_________________________.
11.如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加的一个条件是________________.
12.如图,△ABC和△ABD中,∠C=∠D=90°,要证明△ABC≌△ABD,还需要的条件是______.(只需填一个即可)
13.已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.
14.如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于________.
三、解答题
15.如图,点分别是对角线上两点,.求证:.
16.已知:如图,在△ABC中,O是边BC的中点,E是线段AB延长线上一点,过点C作CD∥BE,交线段EO的延长线于点D,连接BD,CE.
(1)求证:CD=BE;
(2)如果∠ABD=2∠BED,求证:四边形BECD是菱形.
17.如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:BC=DE
(2)若∠A=40°,求∠BCD的度数.
18.(本题满分10分)如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.
求证:(1)求证:△ABE≌△ACD;
(2)求证:四边形BCDE是矩形.
参考答案
1.B
【解析】
试题解析:连接AC,
∵AB=CD,BC=AD(已知),
AC=AC,
∴△ABC≌△ACD,
故选B.
2.C
【解析】
【分析】
根据∠1=∠2可利用等式的性质得到∠BAC=∠DAE,然后再根据所给的条件利用全等三角形的判定定理进行分析即可.
【详解】
解:∵∠1=∠2, ∴∠1+∠DAC=∠2+∠DAC, ∴∠BAC=∠DAE, A、添加AE=AC,可利用SAS定理判定△ABC≌△ADE,故此选项不合题意; B、添加∠B=∠D,可利用SAS定理判定△ABC≌△ADE,故此选项不合题意; C、添加BC=DE,不能判定△ABC≌△ADE,故此选项符合题意; D、添加∠C=∠E,可利用AAS定理判定△ABC≌△ADE,故此选项不合题意; 故选C.
【点睛】
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
3.B
【解析】
【分析】
根据确定三角形全等的条件进行判定即可得解.
【详解】
解:根据伞的结构,AE=AF,伞骨DE=DF,AD是公共边, ∵在△ADE和△ADF中,
∴△ADE≌△ADF(SSS), ∴∠DAE=∠DAF, 即AP平分∠BAC. 故选:B.
【点睛】
本题考查了全等三角形的应用,理解题意确定出全等的三角形以及全等的条件是解题的关键.
4.A
【解析】
【分析】
根据全等三角形的判定对各选项进行分析.
【详解】
∵BD是∠ABE的角平分线,
∴∠ABD=∠EBD,且BD是公共边,
A选项:若AD=ED,则SSA,不能判定三角形全等,故符合题意;
B选项:若AB=EB,根据SAS可以判定三角形全等,故不符合题意;
C选项:若DB平分∠ADE,则∠ADB=∠EDB,根据ASA可判定三角形全等,故不符合题意;
D选项:若∠A=∠BED,根据AAS可判定三角形全等,故不符合题意;
故选:A.
【点睛】
考查了全等三角形的判定:判定三角形全等的方法有“SSS”、“AAS”、“SAS”、“ASA”.
5.C
【解析】
∵∠CAB=∠DBA,AB=BA, ∴当AC=BD时,依据SAS能使△ABC≌△BAD;当∠C=∠D时,依据AAS能使△ABC≌△BAD;当∠CBD=∠DAC时,∠ABC=∠BAD,依据ASA能使△ABC≌△BAD;当BC=AD时,不一定能使△ABC≌△BAD;故选:C.
6.C
【解析】
如图,∵AB=DE,∠A=∠D,
∴根据“边角边”可添加AC=DF,
根据“角边角”可添加∠B=∠E,
根据“角角边”可添加∠C=∠F.
所以补充①③④可判定△ABC≌△DEF.
故选C.
7.B
【解析】
【分析】
根据全等三角形的判定,逐个分析即可.
【详解】
A. AB=DE,AC=DF, 且∠A=∠D=90°,根据SAS,△ABC和△DEF全等;
B. AC=EF,BC=DF , 且∠A=∠D=90°,不能判定△ABC和△DEF全等;
C. AB=DE,BC=EF ,且∠A=∠D=90°,根据HL,△ABC和△DEF全等;
D. ∠C=∠F,BC=EF, 且∠A=∠D=90°,根据AAS,△ABC和△DEF全等.
故选B
【点睛】
本题考核知识点:全等三角形的判定. 解题关键点:熟记全等三角形的判定.
8.D
【解析】
分析:①用HL证明△ABG≌△AFG;②由△ADE≌△AFE,△ABG≌△AFG,得到∠EAG=∠BAD;③在直角三角形CEG中,由勾股定理求GC的长;④根据基本图形“等腰三角形+角平分线→平行线”证明;⑤由GF:EG=3:5,得S△FCG:S△ECG=3:5.
详解:①根据轴对称的性质得,△ADE≌△AFE,
所以AD=AF,∠AFE=∠D=90°.
因为AB=AD,∠B=90°,所以AB=AF,
因为AG=AG,所以△ABG≌△AFG.
则①正确;
②因为△ADE≌△AFE,△ABG≌△AFG,
所以∠DAE=∠FAE,∠BAG=∠FAG,
所以∠EAG=∠FAE+∠FAE=∠BAD=×90°=45°.
则②正确;
③因为△ADE≌△AFE,△ABG≌△AFG,
所以ED=EF,GB=GF,所以EG=DE+BG,
设BG=x,则CG=FG=6-x,DE=2,CE=4,EG=x+2=x+2.
Rt△CEG中,由勾股定理得,CG2+CE2=EG2,
所以(6-x)2+42=(x+2)2,解得x=3.
则CG=6-x=3,又BG=x=3,所以BG=CG.
则③正确;
④因为△ABG≌△AFG,所以∠AGB=∠AGF.
因为BG=CG,BG=GF,所以CG=GF,所以∠GCF=∠GFC.
因为∠BGE=∠GCF+∠GFC,所以∠AGB=∠GCF,所以AG∥CF.
则④正确;
⑤因为GF=3,GE=5,所以S△FGC=S△GCE=×GC·CE=××3×4=3.6.
则⑤正确.
故选D.
点睛:正方形的折叠问题中涉及到线段的长一般用勾股定理列方程求解,要熟悉基本图形“角平分线+平行线→等腰三角形”,把“角平分线”,“平行线”,“等腰三角形”,这三个中的任意两个作为题设,另一个作为结论所得的命题都是真命题.
9.2 角边角
【解析】
【分析】
本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.
【详解】
1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的。
故答案为:2.
【点睛】
考查全等三角形的判定,掌握全等三角形的判定定理是解题的关键.
10.(2,4)或(4,2).
【解析】
试题分析:①当点P在正方形的边AB上时,在Rt△OCD和Rt△OAP中,∵OC=OA,CD=OP,∴Rt△OCD≌Rt△OAP,∴OD=AP,∵点D是OA中点,∴OD=AD=OA,∴AP=AB=2,∴P(4,2);
②当点P在正方形的边BC上时,同①的方法,得出CP=BC=2,∴P(2,4).
综上所述:P(2,4)或(4,2).故答案为(2,4)或(4,2).
考点:全等三角形的判定与性质;坐标与图形性质;分类讨论.
11.AB=CD或∠E=∠F(答案不唯一)
【解析】
分析:添加条件AB=CD可证明AC=BD,然后再根据AE∥FD,可得∠A=∠D,再利用SAS定理证明△EAC≌△FDB即可.
详解:∵AE∥FD,
∴∠A=∠D,
∵AB=CD,
∴AC=BD,
在△AEC和△DFB中,
,
∴△EAC≌△FDB(SAS),
故答案为:AB=CD.
点睛:此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
12.AC=AD
【解析】
【分析】
根据∠C=∠D=90°利用HL定理推出两三角形全等即可.
【详解】
添加的条件是AC=AD,理由是:
∵∠C=∠D=90°,
∴在Rt△ACB和Rt△ADB中
,
∴Rt△ACB≌Rt△ADB(HL).
故答案为AD=AC.
【点睛】
本题考查了全等三角形的判定定理的应用,注意两直角三角形全等的方法有SAS,ASA,AAS,SSS,HL,此题是一道开放性的题目,答案不唯一.
13.5
【解析】
【分析】
根据正方形的四条边都相等可得AB=AD,每一个角都是直角可得∠BAE=∠D=90°;然后利用“边角边”证明△ABE≌△DAF得∠ABE=∠DAF,进一步得∠AGE=∠BGF=90°,从而知GH=BF,利用勾股定理求出BF的长即可得出答案.
【详解】
∵四边形ABCD为正方形, ∴∠BAE=∠D=90°,AB=AD, 在△ABE和△DAF中,∵AB=AD,∠BAE=∠D,AE=DF, ∴△ABE≌△DAF(SAS), ∴∠ABE=∠DAF, ∵∠ABE+∠BEA=90°, ∴∠DAF+∠BEA=90°, ∴∠AGE=∠BGF=90°, ∵点H为BF的中点, ∴GH=BF, ∵BC=8,CF=CD-DF=8-2=6, ∴BF==10, ∴GH=BF=5.
【点睛】
本题考查了正方形的性质,全等三角形的判定与性质,直角三角形两锐角互余等知识,掌握三角形全等的判定方法与正方形的性质是解题的关键.
14.7
【解析】
考点:矩形的性质;平行四边形的判定与性质.
分析:连接EG,FH,根据题目数据可以证明△AEF与△CGH全等,根据全等三角形对应边相等可得EF=GH,同理可得EG=FH,然后根据两组对边相等的四边形是平行四边形可得四边形EGHF是平行四边形,所以△PEF和△PGH的面积和等于平行四边形EGHF的面积的一半,再利用平行四边形EGHF的面积等于矩形ABCD的面积减去四周四个小直角三角形的面积即可求解.
解:∵在矩形ABCD中,AD=6,AB=4,AF=CG=2,BE=DH=1,
∴AE=AB-BE=4-1=3,
CH=CD-DH=4-1=3,
∴AE=CH,
在△AEF与△CGH中,,
∴△AEF≌△CGH(SAS),
∴EF=GH,
同理可得,△BGE≌△DFH,
∴EG=FH,
∴四边形EGHF是平行四边形,
∵△PEF和△PGH的高的和等于点H到直线EF的距离,
∴△PEF和△PGH的面积和=×平行四边形EGHF的面积,
平行四边形EGHF的面积
=4×6-×2×3-×1×(6-2)-×2×3-×1×(6-2),
=24-3-2-3-2,
=14,
∴△PEF和△PGH的面积和=×14=7.
故答案为7.
15.见解析
【解析】
【分析】
用SAS证明△BAF≌△DCE即可说明∠DEC=∠BFA.
【详解】
证明::∵四边形为平行四边形,
∴,
∴,
又,
∴≌,
∴.
【点睛】
本题主要考查了平行四边形的性质、全等三角形的判定和性质,解决这类问题一般是四边形转化为三角形处理.
16.见解析
【解析】
【分析】
(1)可通过全等三角形来证明简单的线段相等,△COD和△BOE中,已知了CO=BO,∠COD=∠BOE,CD∥BE,因此不难得出两三角形全等,进而可得出CD=BE.
(2)需先证明四边形AFCE是平行四边形,那么邻边相等的平行四边形是菱形.
【详解】
(1)∵CD∥BE,
∴∠CDE=∠DEB.
∵O是边BC的中点,
∴CO=BO.
在△COD和△BOE中,
∴△COD≌△BOE(AAS).
∴CD=BE.
(2)∵CD∥BE,CD=BE,
∴四边形BECD是平行四边形.
∵∠ABD=2∠BED,∠ABD=∠BED+∠BDE,
∴∠BED=∠BDE.
∴BD=BE.
∴四边形BECD是菱形.
点睛:本题考查了平行线的性质,平行四边形的判定,菱形的判定,全等三角形的判定与性质,注意掌握两条线段在不同的三角形中要证明相等时,通常是利用全等来进行证明.
17.(1)证明见解析;(2)140°;
【解析】
【分析】
(1)根据平行线的性质可得∠ACB=∠DEC,∠ACD=∠D,再由∠ACD=∠B可得∠D=∠B,然后可利用AAS证明△ABC≌△CDE,进而得到CB=DE; (2)根据全等三角形的性质可得∠A=∠DCE=40°,然后根据邻补角的性质进行计算即可.
【详解】
(1)∵AC∥DE,
∴∠ACB=∠DEC,∠ACD=∠D,
∵∠ACD=∠B.
∴∠D=∠B,
在△ABC和△DEC中,,
∴△ABC≌△CDE(AAS),
∴BC=DE;
(2)∵△ABC≌△CDE,
∴∠A=∠DCE=40°
∴∠BCD=180°–40°=140°.
【点睛】
本题考查的是全等三角形,熟练掌握全等三角形的性质是解题的关键.
18.(1)见解析;(2)见解析
【解析】
试题分析:(1)根据条件∠BAD=∠CAE证出∠EAB=∠DAC即可用SAS证明△ABE≌△ACD;(2)由(1)可得BE=CD,进而可证四边形BCDE为平行四边形,然后再证明∠DCB=90°即可.
试题解析:(1)证明:∵∠BAD=∠CAE ∴∠EAB=∠DAC,在△ABE和△ACD中
∵AB=AC,∠EAB=∠DAC,AE=AD
∴△ABE≌△ACD(SAS)
(2)∵△ABE≌△ACD ∴BE=CD,又DE=BC
∴四边形BCDE为平行四边形.
∵AB=AC,∴∠ABC=∠ACB
∵△ABE≌△ACD∴∠ABE=∠ACD∴∠EBC=∠DCB
∵四边形BCDE为平行四边形∴EB∥DC∴∠EBC+∠DCB=180°
∴∠EBC=∠DCB=90°
四边形BCDE是矩形.
(此题也可连接EC,DB,通过全等,利用对角线相当的平行四边形是矩形进行证明)
考点:1.全等三角形的判定与性质;2.矩形的判定.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
