北师大版七年级数学下册同步精练专题 5.4利用轴对称进行设计同步训练(含解析)
文档属性
| 名称 | 北师大版七年级数学下册同步精练专题 5.4利用轴对称进行设计同步训练(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 427.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-17 00:00:00 | ||
图片预览



文档简介
5.4利用轴对称进行设计同步训练
学校:___________姓名:___________班级:___________考号:___________
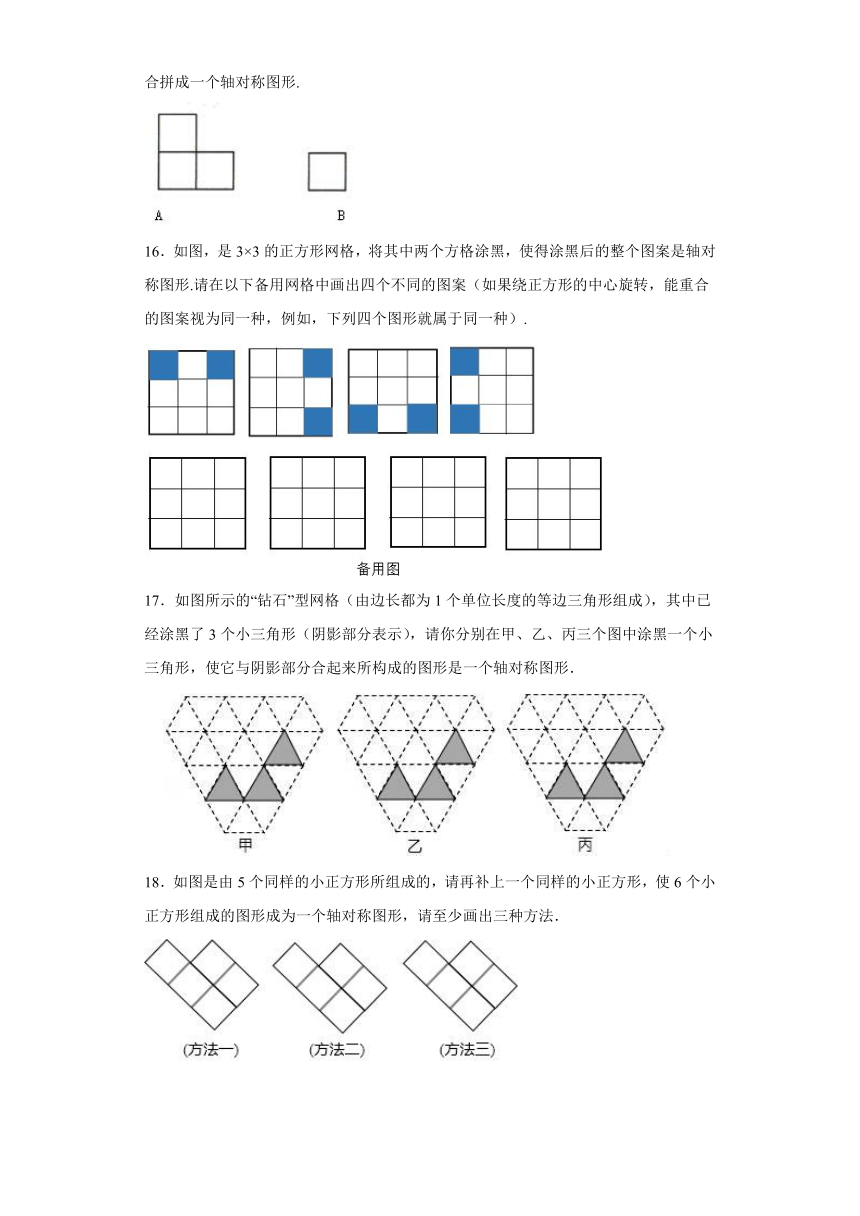
一、单选题
1.在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用轴对称知识的是 ( )
A. B.
C. D.
2.如图,已知要在一块长方形的空地上修建一个花坛,要求花坛图案(阴影部分)为轴对称图形,图中的设计符合要求的有( )
A.4个 B.3个 C.2个 D.1个
3.在3×3的正方形网格中,将三个小正方形涂色如图所示,若移动其中一个涂色小正方形到空白方格中,与其余两个涂色小正方形重新组合,使得新构成的整个图案是一个轴对称图形,则这样的移法共有(?? )
A.5种
B.7种
C.9种
D.10种
4.如图2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有 ( )
A.2个 B.3个 C.5个 D.7个
5.如图,将甲图经图形变换变到乙图,下列说法错误的是( )
A.可以通过旋转和平移实现 B.可以通过旋转和轴对称实现
C.必须通过旋转才能实现 D.不必通过旋转就能实现
6.下列都是同学们喜欢的商标,其中是轴对称图形的是( )
A. B. C. D.
7.如图所示是4×5的方格纸,请在其中选取一个白色的方格并涂黑,使图中阴影部分是一个轴对称图形,这样的涂法有( )
A.4种 B.3种 C.2种 D.1种
8.如图,在的正方形网格中,有一个格点(阴影部分),则网格中所有与成轴对称的格点三角形的个数为( )
A.2 B.3 C.4 D.5
二、填空题
9.如图是一组按照某种规律摆放成的图案,则第2019个图案____轴对称图形(填“是”或“不是”).
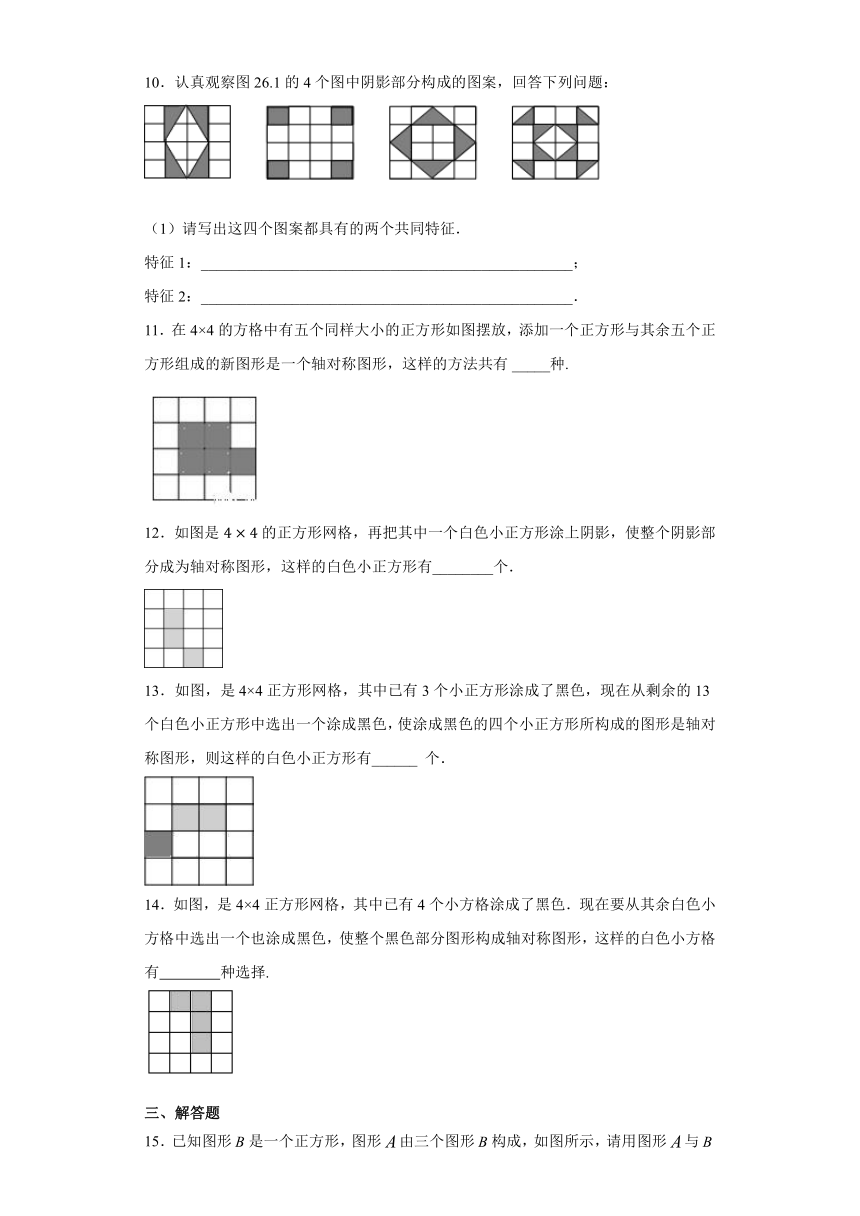
10.认真观察图26.1的4个图中阴影部分构成的图案,回答下列问题:
(1)请写出这四个图案都具有的两个共同特征.
特征1:_________________________________________________;
特征2:_________________________________________________.
11.在4×4的方格中有五个同样大小的正方形如图摆放,添加一个正方形与其余五个正方形组成的新图形是一个轴对称图形,这样的方法共有?_____种.?
12.如图是4×4的正方形网格,再把其中一个白色小正方形涂上阴影,使整个阴影部分成为轴对称图形,这样的白色小正方形有________个.
13.如图,是4×4正方形网格,其中已有3个小正方形涂成了黑色,现在从剩余的13个白色小正方形中选出一个涂成黑色,使涂成黑色的四个小正方形所构成的图形是轴对称图形,则这样的白色小正方形有______ 个.
14.如图,是4×4正方形网格,其中已有4个小方格涂成了黑色.现在要从其余白色小方格中选出一个也涂成黑色,使整个黑色部分图形构成轴对称图形,这样的白色小方格有 种选择.
三、解答题
15.已知图形是一个正方形,图形由三个图形构成,如图所示,请用图形与合拼成一个轴对称图形.
16.如图,是3×3的正方形网格,将其中两个方格涂黑,使得涂黑后的整个图案是轴对称图形.请在以下备用网格中画出四个不同的图案(如果绕正方形的中心旋转,能重合的图案视为同一种,例如,下列四个图形就属于同一种).
17.如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你分别在甲、乙、丙三个图中涂黑一个小三角形,使它与阴影部分合起来所构成的图形是一个轴对称图形.
18.如图是由5个同样的小正方形所组成的,请再补上一个同样的小正方形,使6个小正方形组成的图形成为一个轴对称图形,请至少画出三种方法.
参考答案
1.C
【解析】
试题分析:根据轴对称及旋转对称的定义,结合各选项进行判断即可.
解:A、即运用了轴对称也利用了旋转对称,故本选项错误;
B、利用了轴对称,故本选项错误;
C、没有运用旋转,也没有运用轴对称,故本选项正确;
D、即运用了轴对称也利用了旋转对称,故本选项错误;
故选C.
点评:本题考查了轴对称及旋转对称的知识,解答本题的关键是掌握轴对称及旋转对称的定义.
2.A
【解析】
根据轴对称图形的概念即可判定.
解:四副设计图中的阴影部分均为轴对称图形,故满足设计要求的图形有4个.
故选A.
3.D
【解析】
【分析】
利用轴对称的性质,以及轴对称的作图方法来作图,通过变换对称轴来得到不同的图案即可.
【详解】
如图所示:一共有10种轴对称图形.
故选:D.
【点睛】
此题考查利用轴对称设计图案,解题关键在于掌握其性质.
4.B
【解析】
【分析】
根据轴对称的性质,结合网格结构,分横向和纵向两种情况确定出不同的对称轴的位置,然后作出与△ABC成轴对称的格点三角形,从而得解.
【详解】
如图所示,对称轴有三种位置,与△ABC成轴对称的格点三角形有3个,
故选B.
【点睛】
此题考查轴对称的性质,解题关键在于画出图形.
5.D
【解析】
【分析】
结合图形特点可得甲图形变为乙图形可以经过旋转、平移或旋转、轴对称实现,从而可得出答案.
【详解】
甲图形变为乙图形必须通过旋转变换,
所以D选项错误,
故选D.
【点睛】
本题考查了几何变换的类型,属于基础题,掌握各几何变换的特点是解答本题的关键.
6.B
【解析】
【分析】
沿某条直线折叠后直线两旁的部分能够完全重合,则这个图形是轴对称图形;
接下来,根据轴对称图形的定义,结合选项,一一进行判断即可.
【详解】
根据轴对称图形的定义可得只有选项B中的图形是轴对称图形.
故答案选B.
【点睛】
本题考查了轴对称图形的有关知识,解题的关键是熟练的掌握轴对称图形的定义.
7.B
【解析】
【分析】
结合图象根据轴对称图形的概念求解即可.
【详解】
根据轴对称图形的概念可知,一共有3种涂法,如下图所示:
.
故选B.
【点睛】
本题考查了轴对称图形的知识,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
8.D
【解析】
【分析】
因为对称图形是全等的,所以面积相等,据此连接矩形的对角线,观察得到的三角形即可解答.
【详解】
如图,与△ABC成轴对称的格点三角形有△ACF、△ACD、△DBC,△HEG,△HBG共5个,
故选D.
【点睛】
此题考查利用轴对称设计图案.
9.是
【解析】
【分析】
作出前四个图形的对称轴,类推即可得出结论.
【详解】
前四个图形的对称轴如下:
由此可得按此规律摆放成的图案都是轴对称图形.
故答案为:是.
【点睛】
本题考查了图形的变化规律以及轴对称图形,注意由特殊到一般的分析方法.这类题型在中考中经常出现.
10.都是轴对称图形;都是中心对称图形.
【解析】
【分析】
利用沿某条直线折叠后直线两旁的部分能够完全重合的图形叫做轴对称图形.绕一个点旋转180度后所得的图形与原图形完全重合的图形叫做中心对称图形,进而得出即可.
【详解】
特征1:都是轴对称图形;
特征2:都是中心对称图形.
故答案为:都是轴对称图形;都是中心对称图形.
【点睛】
此题考查利用轴对称设计图案,解题关键在于掌握图形的识别.
11.4
【解析】
【分析】
因为中间4个小正方形组成一个大的正方形,正方形有四条对称轴,试着利用这四条对称轴添加图形得出答案即可.
【详解】
如图所示。
这样的添法共有4种。
故答案为:4.
【点睛】
此题考查利用轴对称设计图案,难度不大
12.4
【解析】
试题解析:如图所示:
,
可得这样的白色的小正方形有4个.
考点:轴对称图形.
13.4
【解析】
【分析】
根据轴对称图形的概念求解即可.
【详解】
解:如图所示,有4个位置使之成为轴对称图形.
故答案为:4.
【点睛】
本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
14.3
【解析】
如下图,这样的白色小方格共有3种选择.
15.见解析
【解析】
【分析】
由于小正方形是轴对称图形,所以只要构成的大图对称即可.
【详解】
解,如图:
【点睛】
解答此题要明确轴对称图形的定义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形.
16.见解析
【解析】
【分析】
根据轴对称的性质画出图形即可.
【详解】
如图所示.
【点睛】
本题考查了利用轴对称设计图案,培养学生实际操作能力,用到了图形的旋转及轴对称的知识,需要灵活掌握.
17.见解析;
【解析】
【分析】
根据轴对称的性质进行作图即可.
【详解】
如图所示:
【点睛】
考查利用轴对称设计图案,熟练掌握轴对称图形的定义是解题的关键.
18.见解析
【解析】
【分析】
利用轴对称图形的性质得出符合题意的答案,如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.
【详解】
如图所示:
.
【点睛】
此题主要考查了利用轴对称设计图案,正确掌握轴对称图形的性质是解题关键.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用轴对称知识的是 ( )
A. B.
C. D.
2.如图,已知要在一块长方形的空地上修建一个花坛,要求花坛图案(阴影部分)为轴对称图形,图中的设计符合要求的有( )
A.4个 B.3个 C.2个 D.1个
3.在3×3的正方形网格中,将三个小正方形涂色如图所示,若移动其中一个涂色小正方形到空白方格中,与其余两个涂色小正方形重新组合,使得新构成的整个图案是一个轴对称图形,则这样的移法共有(?? )
A.5种
B.7种
C.9种
D.10种
4.如图2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有 ( )
A.2个 B.3个 C.5个 D.7个
5.如图,将甲图经图形变换变到乙图,下列说法错误的是( )
A.可以通过旋转和平移实现 B.可以通过旋转和轴对称实现
C.必须通过旋转才能实现 D.不必通过旋转就能实现
6.下列都是同学们喜欢的商标,其中是轴对称图形的是( )
A. B. C. D.
7.如图所示是4×5的方格纸,请在其中选取一个白色的方格并涂黑,使图中阴影部分是一个轴对称图形,这样的涂法有( )
A.4种 B.3种 C.2种 D.1种
8.如图,在的正方形网格中,有一个格点(阴影部分),则网格中所有与成轴对称的格点三角形的个数为( )
A.2 B.3 C.4 D.5
二、填空题
9.如图是一组按照某种规律摆放成的图案,则第2019个图案____轴对称图形(填“是”或“不是”).
10.认真观察图26.1的4个图中阴影部分构成的图案,回答下列问题:
(1)请写出这四个图案都具有的两个共同特征.
特征1:_________________________________________________;
特征2:_________________________________________________.
11.在4×4的方格中有五个同样大小的正方形如图摆放,添加一个正方形与其余五个正方形组成的新图形是一个轴对称图形,这样的方法共有?_____种.?
12.如图是4×4的正方形网格,再把其中一个白色小正方形涂上阴影,使整个阴影部分成为轴对称图形,这样的白色小正方形有________个.
13.如图,是4×4正方形网格,其中已有3个小正方形涂成了黑色,现在从剩余的13个白色小正方形中选出一个涂成黑色,使涂成黑色的四个小正方形所构成的图形是轴对称图形,则这样的白色小正方形有______ 个.
14.如图,是4×4正方形网格,其中已有4个小方格涂成了黑色.现在要从其余白色小方格中选出一个也涂成黑色,使整个黑色部分图形构成轴对称图形,这样的白色小方格有 种选择.
三、解答题
15.已知图形是一个正方形,图形由三个图形构成,如图所示,请用图形与合拼成一个轴对称图形.
16.如图,是3×3的正方形网格,将其中两个方格涂黑,使得涂黑后的整个图案是轴对称图形.请在以下备用网格中画出四个不同的图案(如果绕正方形的中心旋转,能重合的图案视为同一种,例如,下列四个图形就属于同一种).
17.如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你分别在甲、乙、丙三个图中涂黑一个小三角形,使它与阴影部分合起来所构成的图形是一个轴对称图形.
18.如图是由5个同样的小正方形所组成的,请再补上一个同样的小正方形,使6个小正方形组成的图形成为一个轴对称图形,请至少画出三种方法.
参考答案
1.C
【解析】
试题分析:根据轴对称及旋转对称的定义,结合各选项进行判断即可.
解:A、即运用了轴对称也利用了旋转对称,故本选项错误;
B、利用了轴对称,故本选项错误;
C、没有运用旋转,也没有运用轴对称,故本选项正确;
D、即运用了轴对称也利用了旋转对称,故本选项错误;
故选C.
点评:本题考查了轴对称及旋转对称的知识,解答本题的关键是掌握轴对称及旋转对称的定义.
2.A
【解析】
根据轴对称图形的概念即可判定.
解:四副设计图中的阴影部分均为轴对称图形,故满足设计要求的图形有4个.
故选A.
3.D
【解析】
【分析】
利用轴对称的性质,以及轴对称的作图方法来作图,通过变换对称轴来得到不同的图案即可.
【详解】
如图所示:一共有10种轴对称图形.
故选:D.
【点睛】
此题考查利用轴对称设计图案,解题关键在于掌握其性质.
4.B
【解析】
【分析】
根据轴对称的性质,结合网格结构,分横向和纵向两种情况确定出不同的对称轴的位置,然后作出与△ABC成轴对称的格点三角形,从而得解.
【详解】
如图所示,对称轴有三种位置,与△ABC成轴对称的格点三角形有3个,
故选B.
【点睛】
此题考查轴对称的性质,解题关键在于画出图形.
5.D
【解析】
【分析】
结合图形特点可得甲图形变为乙图形可以经过旋转、平移或旋转、轴对称实现,从而可得出答案.
【详解】
甲图形变为乙图形必须通过旋转变换,
所以D选项错误,
故选D.
【点睛】
本题考查了几何变换的类型,属于基础题,掌握各几何变换的特点是解答本题的关键.
6.B
【解析】
【分析】
沿某条直线折叠后直线两旁的部分能够完全重合,则这个图形是轴对称图形;
接下来,根据轴对称图形的定义,结合选项,一一进行判断即可.
【详解】
根据轴对称图形的定义可得只有选项B中的图形是轴对称图形.
故答案选B.
【点睛】
本题考查了轴对称图形的有关知识,解题的关键是熟练的掌握轴对称图形的定义.
7.B
【解析】
【分析】
结合图象根据轴对称图形的概念求解即可.
【详解】
根据轴对称图形的概念可知,一共有3种涂法,如下图所示:
.
故选B.
【点睛】
本题考查了轴对称图形的知识,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
8.D
【解析】
【分析】
因为对称图形是全等的,所以面积相等,据此连接矩形的对角线,观察得到的三角形即可解答.
【详解】
如图,与△ABC成轴对称的格点三角形有△ACF、△ACD、△DBC,△HEG,△HBG共5个,
故选D.
【点睛】
此题考查利用轴对称设计图案.
9.是
【解析】
【分析】
作出前四个图形的对称轴,类推即可得出结论.
【详解】
前四个图形的对称轴如下:
由此可得按此规律摆放成的图案都是轴对称图形.
故答案为:是.
【点睛】
本题考查了图形的变化规律以及轴对称图形,注意由特殊到一般的分析方法.这类题型在中考中经常出现.
10.都是轴对称图形;都是中心对称图形.
【解析】
【分析】
利用沿某条直线折叠后直线两旁的部分能够完全重合的图形叫做轴对称图形.绕一个点旋转180度后所得的图形与原图形完全重合的图形叫做中心对称图形,进而得出即可.
【详解】
特征1:都是轴对称图形;
特征2:都是中心对称图形.
故答案为:都是轴对称图形;都是中心对称图形.
【点睛】
此题考查利用轴对称设计图案,解题关键在于掌握图形的识别.
11.4
【解析】
【分析】
因为中间4个小正方形组成一个大的正方形,正方形有四条对称轴,试着利用这四条对称轴添加图形得出答案即可.
【详解】
如图所示。
这样的添法共有4种。
故答案为:4.
【点睛】
此题考查利用轴对称设计图案,难度不大
12.4
【解析】
试题解析:如图所示:
,
可得这样的白色的小正方形有4个.
考点:轴对称图形.
13.4
【解析】
【分析】
根据轴对称图形的概念求解即可.
【详解】
解:如图所示,有4个位置使之成为轴对称图形.
故答案为:4.
【点睛】
本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
14.3
【解析】
如下图,这样的白色小方格共有3种选择.
15.见解析
【解析】
【分析】
由于小正方形是轴对称图形,所以只要构成的大图对称即可.
【详解】
解,如图:
【点睛】
解答此题要明确轴对称图形的定义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形.
16.见解析
【解析】
【分析】
根据轴对称的性质画出图形即可.
【详解】
如图所示.
【点睛】
本题考查了利用轴对称设计图案,培养学生实际操作能力,用到了图形的旋转及轴对称的知识,需要灵活掌握.
17.见解析;
【解析】
【分析】
根据轴对称的性质进行作图即可.
【详解】
如图所示:
【点睛】
考查利用轴对称设计图案,熟练掌握轴对称图形的定义是解题的关键.
18.见解析
【解析】
【分析】
利用轴对称图形的性质得出符合题意的答案,如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.
【详解】
如图所示:
.
【点睛】
此题主要考查了利用轴对称设计图案,正确掌握轴对称图形的性质是解题关键.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
