人教版八年级数学下册16.1二次根式上课课件(22张PPT)
文档属性
| 名称 | 人教版八年级数学下册16.1二次根式上课课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 332.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-17 19:31:01 | ||
图片预览







文档简介
(共22张PPT)
16.1 二次根式
⑵什么是一个数的算术平方根?如何表示?
一个正数a的正的平方根叫做它的算术平方根.
回忆
⑴什么叫做一个数的平方根?如何表示?
一般地,若一个数的平方等于a,则
这个数就叫做a的平方根.
用 (a≥0)表示正数a的算术平方根.
0的算术平方根是0
a的平方根是
求下列各数的平方根和算术平方根.
9 的平方根 , 算术平方根 ;
0.64 的平方根 ,算术平方根 ;
0 的平方根 ,算术平方根 .
0.8
0
0
3
a(a≥0)的平方根 ,
a的算术平方根是 .
一个正数有两个平方根, 它们互为相反数;
0的平方根是0;
负数没有平方根。
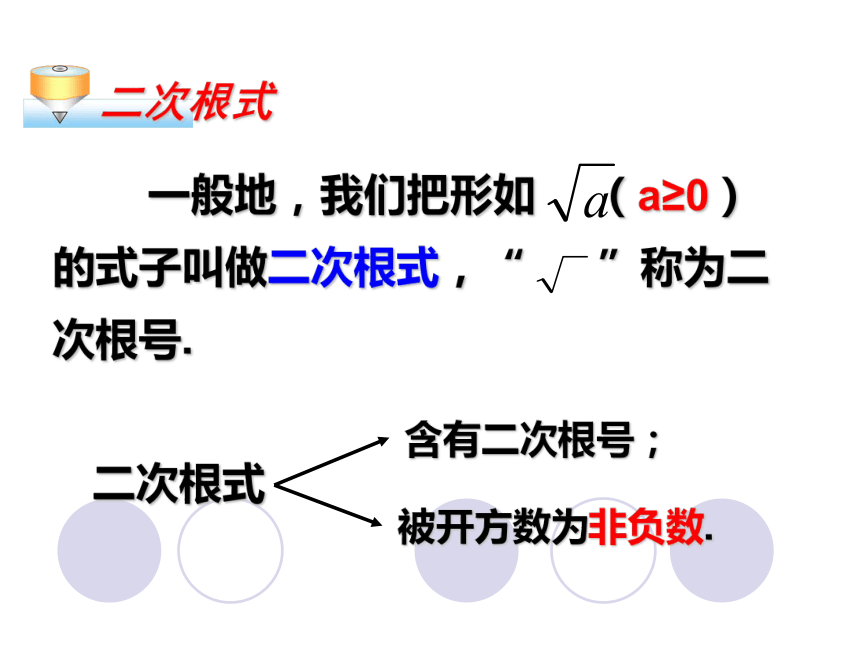
一般地,我们把形如 (a≥0)的式子叫做二次根式,“ ”称为二次根号.
二次根式
被开方数为非负数.
含有二次根号;
二次根式
指出下列哪些是二次根式?
√
√
√
√
二次根式满足的两个条件是:
(1)有二次根号;
(2)被开方数是非负数.
二次根式的双重非负性:
双重非负性
≥0
被开方数a≥0
二次根式
探究:利用算术平方根的意义填空:
0
4
0.01
一般地,有
(a≥0)
性质1
x+3≥0
∴x≥-3
∴当x≥-3时, 在实数范围内有意义.
例1.当x为何值时,下列各式在实数范围内有意义?
解:(1)由题意,得
(2)因为x为人何实数时都有
所以当x为一切实数时, 都有意义.
1.求下列二次根式中字母的取值范围:
求二次根式中字母的取值范围的基本依据:
①被开方数大于等于零;
②分母中有字母时,要保证分母不为零。
跟进训练
方法构想
(a≥0)
(a可取任意实数)
2.当x取怎样的实数时,
有意义?
解:由题意得
∴
方法构想
一个式子中:
若含有几个二次根式,则要求所有被开方数大于等于0;
若含有分式,则要求分母的值不等于0;
若含有零指数或负指数次幂,则要求其底数不为0.
∴
X≥
X ≠-1
3.当x为怎样的实数时,下列各式有意义?
x≥3
x≤6
∴3≤x≤6
x≥1
x≤1
∴x=1
x为全体实数.
x为全体实数.
一般地,有
性质2
又如
再计算如下根式时
例2:
解:
例3 先化简再求值: ,其中 x=4.
当 x=4时, .
解:
∴当x=4时, .
练习
=8
=3
=12
= -6
1.计算:
=3
解:
方法构想:
例4:
如果几个非负数(a2 、|a|、 )的和为0,
那么每一个非负数都是0.
解:
∴a的值为-1,b的值为-2.
中考链接:
.
3
解:由题意得:
a-2=0
b-3=0
c-4=0
a=2
∴ b=3
c=4
1、函数 中,自变量x的取值范围是
.
2、当x取何值时,下列各式在实数范围内有意义?
(1)
(2)
(4)
x≥0且x≠1
归纳
(a≥0)
性质1
性质2
再见
16.1 二次根式
⑵什么是一个数的算术平方根?如何表示?
一个正数a的正的平方根叫做它的算术平方根.
回忆
⑴什么叫做一个数的平方根?如何表示?
一般地,若一个数的平方等于a,则
这个数就叫做a的平方根.
用 (a≥0)表示正数a的算术平方根.
0的算术平方根是0
a的平方根是
求下列各数的平方根和算术平方根.
9 的平方根 , 算术平方根 ;
0.64 的平方根 ,算术平方根 ;
0 的平方根 ,算术平方根 .
0.8
0
0
3
a(a≥0)的平方根 ,
a的算术平方根是 .
一个正数有两个平方根, 它们互为相反数;
0的平方根是0;
负数没有平方根。
一般地,我们把形如 (a≥0)的式子叫做二次根式,“ ”称为二次根号.
二次根式
被开方数为非负数.
含有二次根号;
二次根式
指出下列哪些是二次根式?
√
√
√
√
二次根式满足的两个条件是:
(1)有二次根号;
(2)被开方数是非负数.
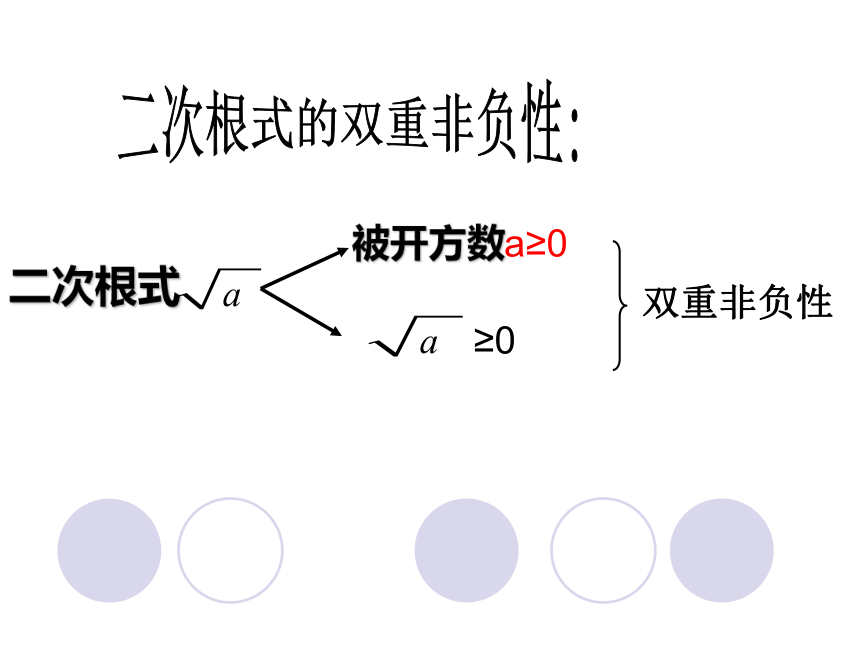
二次根式的双重非负性:
双重非负性
≥0
被开方数a≥0
二次根式
探究:利用算术平方根的意义填空:
0
4
0.01
一般地,有
(a≥0)
性质1
x+3≥0
∴x≥-3
∴当x≥-3时, 在实数范围内有意义.
例1.当x为何值时,下列各式在实数范围内有意义?
解:(1)由题意,得
(2)因为x为人何实数时都有
所以当x为一切实数时, 都有意义.
1.求下列二次根式中字母的取值范围:
求二次根式中字母的取值范围的基本依据:
①被开方数大于等于零;
②分母中有字母时,要保证分母不为零。
跟进训练
方法构想
(a≥0)
(a可取任意实数)
2.当x取怎样的实数时,
有意义?
解:由题意得
∴
方法构想
一个式子中:
若含有几个二次根式,则要求所有被开方数大于等于0;
若含有分式,则要求分母的值不等于0;
若含有零指数或负指数次幂,则要求其底数不为0.
∴
X≥
X ≠-1
3.当x为怎样的实数时,下列各式有意义?
x≥3
x≤6
∴3≤x≤6
x≥1
x≤1
∴x=1
x为全体实数.
x为全体实数.
一般地,有
性质2
又如
再计算如下根式时
例2:
解:
例3 先化简再求值: ,其中 x=4.
当 x=4时, .
解:
∴当x=4时, .
练习
=8
=3
=12
= -6
1.计算:
=3
解:
方法构想:
例4:
如果几个非负数(a2 、|a|、 )的和为0,
那么每一个非负数都是0.
解:
∴a的值为-1,b的值为-2.
中考链接:
.
3
解:由题意得:
a-2=0
b-3=0
c-4=0
a=2
∴ b=3
c=4
1、函数 中,自变量x的取值范围是
.
2、当x取何值时,下列各式在实数范围内有意义?
(1)
(2)
(4)
x≥0且x≠1
归纳
(a≥0)
性质1
性质2
再见
