人教版九年级数学下册26.1.2反比例函数的图象和性质2 课件(含动画 共35张PPT)
文档属性
| 名称 | 人教版九年级数学下册26.1.2反比例函数的图象和性质2 课件(含动画 共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-18 13:01:03 | ||
图片预览








文档简介
(共35张PPT)
? 反比例函数的图象和性质2
知识回顾
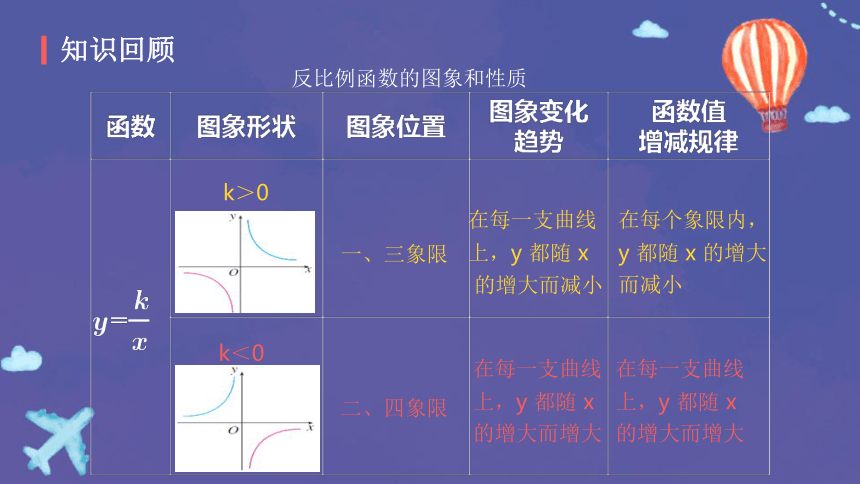
反比例函数的图象和性质
在每一支曲线上,y 都随 x 的增大而增大
在每个象限内,
y 都随 x 的增大
而减小
k>0
一、三象限
在每一支曲线
上,y 都随 x
?的增大而减小
二、四象限
在每一支曲线
上,y 都随 x?
的增大而增大
k<0
黑板上的数
例题
已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限?y随x的增大如何变化?
(2)点B(3,4) 、C(-2.5,-4.8)和D(2,5)是否在这个函数的图象上?
例题
已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限?y随x的增大如何变化?
(2)点B(3,4) 、C(-2.5,-4.8)和D(2,5)是否在这个函数的图象上?
还有什么更简单的方法吗?
可以直接计算点坐标的乘积,看是否等于k即可.
已知反比例函数图象上的点坐标怎么求反比例函数的
解析式呢?
用待定系数法:一设二代,三求四写
如何判断点是否在反比例函数图象上呢?
方法一:把点的横坐标代入解析式算出y,与纵坐标对比
方法二:直接算出点坐标的乘积,与k对比
归纳
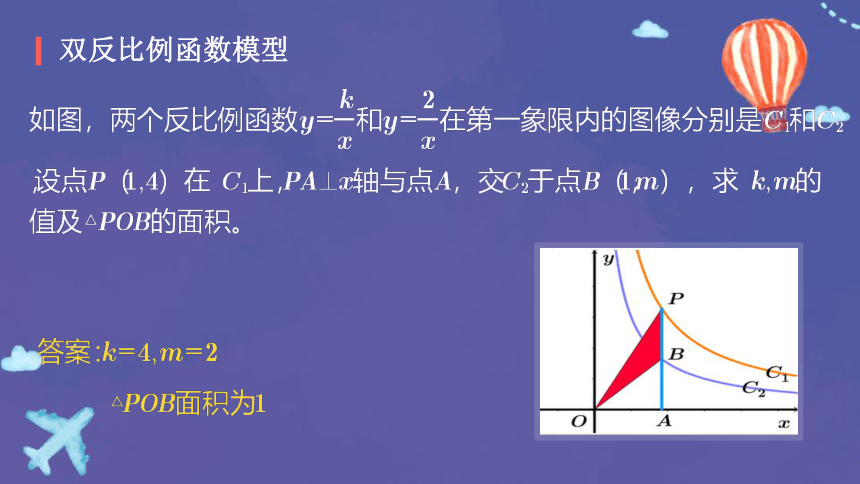
双反比例函数模型
双反比例函数模型
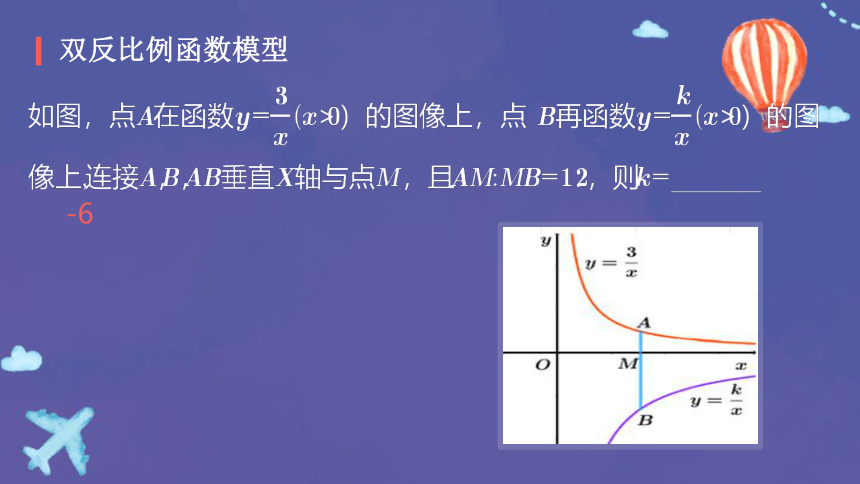
-6
-20
双反比例函数模型
答案:(1)y=x+4;
(2)16.
(1)求这个一次函数的解析式。
(2)求三角形POQ的面积。
反比例函数与一次函数综合
(1)试确定上述反比例函数和一次函数的表达式 ;
反比例函数与一次函数综合
用函数的观点解不等式
用函数的观点解不等式
用函数的观点解不等式
这节课我们学到了什么?
已知反比例函数图象上的点坐标怎么求反比例函数的解析式呢?
用待定系数法:一设二代,三求四写
如何判断点是否在反比例函数图象上呢?
方法一:把点的横坐标代入解析式算出y,与纵坐标对比
方法二:直接算出点坐标的乘积,与k对比
总结
这节课我们学到了什么?
已知 x 的大小怎么比较 y 的大小?
关键是要结合反比例函数的图象.
先根据 x 确定点的相对位置关系,
再根据点的位置比较 y 的大小.
总结
这节课我们还学到了什么?
k的几何意义
矩形面积等于|k|?
三角形的面积等于|k|的一半?
总结
综合运用
综合运用
综合运用
拓广探索
拓广探索
例题
(1)图象的另一支位于哪个象限?常数 m 的取值范围是什么?
解:(1)反比例函数的图像只有两种可能:位于第
第一、三象限,或者第二、四象限.这个函数的图像的一支位于第一象限,
则另一支必位于第三象限.
例题
已知 x 的大小怎么比较 y 的大小?
关键是要结合反比例函数的图象.
先根据 x 确定点的相对位置关系,
再根据点的位置比较 y 的大小.
归纳
练习
① ③
练习
② ④
?
练习
练习
提示:需要分类讨论.?
答案:
补充题
-1
-1<y<0
x<-2 或 x>0
-2<x<0
已知x的范围求y的范围
当x<-2时,y的取值范围是 ___________ ;
当y>-1时,x的取值范围是 _________________,
当y<-1时,x的取值范围是 ______________.
如图,点P是反比例函数? ? ? ? ? ? ?图象上的一点,PA⊥x轴
于A,PB⊥y轴于B.则长方形PAOB的面积为________.
2
总结:
矩形面积等于|k|.
k的几何意义
1
总结:
三角形的面积等于|k|的一半.
k的几何意义
如图,点P是反比例函数? ? ? ? ? ? ?图象上的一点,PD⊥x轴于D.则△POD的面积为________.
如图,点 P 是反比例函数图象上的一点,过点 P 分别向 x 轴、y 轴作垂线,若阴影部分面积为 3,则这个反比例函数的关系式是_________.
K的几何意义
? 反比例函数的图象和性质2
知识回顾
反比例函数的图象和性质
在每一支曲线上,y 都随 x 的增大而增大
在每个象限内,
y 都随 x 的增大
而减小
k>0
一、三象限
在每一支曲线
上,y 都随 x
?的增大而减小
二、四象限
在每一支曲线
上,y 都随 x?
的增大而增大
k<0
黑板上的数
例题
已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限?y随x的增大如何变化?
(2)点B(3,4) 、C(-2.5,-4.8)和D(2,5)是否在这个函数的图象上?
例题
已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限?y随x的增大如何变化?
(2)点B(3,4) 、C(-2.5,-4.8)和D(2,5)是否在这个函数的图象上?
还有什么更简单的方法吗?
可以直接计算点坐标的乘积,看是否等于k即可.
已知反比例函数图象上的点坐标怎么求反比例函数的
解析式呢?
用待定系数法:一设二代,三求四写
如何判断点是否在反比例函数图象上呢?
方法一:把点的横坐标代入解析式算出y,与纵坐标对比
方法二:直接算出点坐标的乘积,与k对比
归纳
双反比例函数模型
双反比例函数模型
-6
-20
双反比例函数模型
答案:(1)y=x+4;
(2)16.
(1)求这个一次函数的解析式。
(2)求三角形POQ的面积。
反比例函数与一次函数综合
(1)试确定上述反比例函数和一次函数的表达式 ;
反比例函数与一次函数综合
用函数的观点解不等式
用函数的观点解不等式
用函数的观点解不等式
这节课我们学到了什么?
已知反比例函数图象上的点坐标怎么求反比例函数的解析式呢?
用待定系数法:一设二代,三求四写
如何判断点是否在反比例函数图象上呢?
方法一:把点的横坐标代入解析式算出y,与纵坐标对比
方法二:直接算出点坐标的乘积,与k对比
总结
这节课我们学到了什么?
已知 x 的大小怎么比较 y 的大小?
关键是要结合反比例函数的图象.
先根据 x 确定点的相对位置关系,
再根据点的位置比较 y 的大小.
总结
这节课我们还学到了什么?
k的几何意义
矩形面积等于|k|?
三角形的面积等于|k|的一半?
总结
综合运用
综合运用
综合运用
拓广探索
拓广探索
例题
(1)图象的另一支位于哪个象限?常数 m 的取值范围是什么?
解:(1)反比例函数的图像只有两种可能:位于第
第一、三象限,或者第二、四象限.这个函数的图像的一支位于第一象限,
则另一支必位于第三象限.
例题
已知 x 的大小怎么比较 y 的大小?
关键是要结合反比例函数的图象.
先根据 x 确定点的相对位置关系,
再根据点的位置比较 y 的大小.
归纳
练习
① ③
练习
② ④
?
练习
练习
提示:需要分类讨论.?
答案:
补充题
-1
-1<y<0
x<-2 或 x>0
-2<x<0
已知x的范围求y的范围
当x<-2时,y的取值范围是 ___________ ;
当y>-1时,x的取值范围是 _________________,
当y<-1时,x的取值范围是 ______________.
如图,点P是反比例函数? ? ? ? ? ? ?图象上的一点,PA⊥x轴
于A,PB⊥y轴于B.则长方形PAOB的面积为________.
2
总结:
矩形面积等于|k|.
k的几何意义
1
总结:
三角形的面积等于|k|的一半.
k的几何意义
如图,点P是反比例函数? ? ? ? ? ? ?图象上的一点,PD⊥x轴于D.则△POD的面积为________.
如图,点 P 是反比例函数图象上的一点,过点 P 分别向 x 轴、y 轴作垂线,若阴影部分面积为 3,则这个反比例函数的关系式是_________.
K的几何意义
