2020春北师大版七下数学:4.5 利用三角形全等测距离 同步练习含答案
文档属性
| 名称 | 2020春北师大版七下数学:4.5 利用三角形全等测距离 同步练习含答案 | 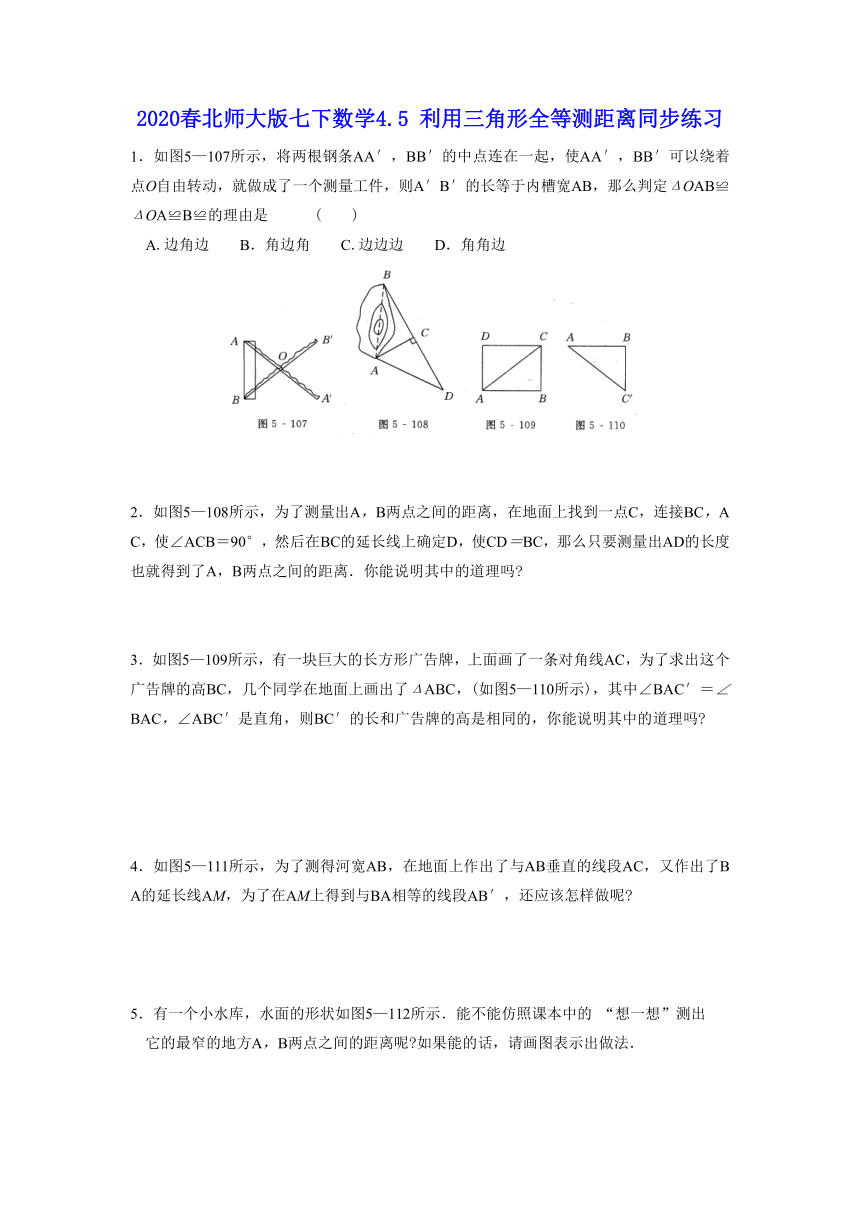 | |
| 格式 | zip | ||
| 文件大小 | 425.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-23 11:54:03 | ||
图片预览



文档简介
2020春北师大版七下数学4.5 利用三角形全等测距离同步练习
1.如图5—107所示,将两根钢条AA′,BB′的中点连在一起,使AA′,BB′可以绕着点O自由转动,就做成了一个测量工件,则A′B′的长等于内槽宽AB,那么判定ΔOAB≌ΔOA≌B≌的理由是 ( )
A.边角边 B.角边角 C.边边边 D.角角边
2.如图5—108所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离.你能说明其中的道理吗?
3.如图5—109所示,有一块巨大的长方形广告牌,上面画了一条对角线AC,为了求出这个广告牌的高BC,几个同学在地面上画出了ΔABC,(如图5—110所示),其中∠BAC′=∠BAC,∠ABC′是直角,则BC′的长和广告牌的高是相同的,你能说明其中的道理吗?
4.如图5—111所示,为了测得河宽AB,在地面上作出了与AB垂直的线段AC,又作出了BA的延长线AM,为了在AM上得到与BA相等的线段AB′,还应该怎样做呢?
5.有一个小水库,水面的形状如图5—112所示.能不能仿照课本中的 “想一想”测出
它的最窄的地方A,B两点之间的距离呢?如果能的话,请画图表示出做法.
6.如图5—113所示,铁路上A,B两站(视为直线上两点)相距14 km,C,D为两村 (可视为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=8 km,CB=6 km,现在要在铁路上建一个土特产品收购站E,使C,D两村到正站的距离相等,则E站应 建在距A站多少千米处?
7.如图5—114所示,A,B两个建筑物分别位于河的两岸,要测得它们之间的距离,
可以从B出发沿河岸画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E,C,A在同一条直线卜,则DE的长就等于A,B之间的距离,请你说明道理.
参考答案
1.A[提示:因为O是AA′和BB′的中点,所以OA=OA′,OB=OB′,且∠AOB=∠A′O B′,符合三角形全等的条件.故选A.]
2.解:因为CD=BC,∠ACD=∠ACB=90°,AC=AC,所以ΔACD≌ΔACB,所以AD=AB.
3.提示:由∠CAB=∠C′AB,AB=AB,∠ABC=∠ABC′知,ΔABC与ΔABC′符合“ASA”,且BC与BC′是对应边,所以BC=BC′.
4.提示:在地面上画射线CB′,与AM相交于B′,使∠ACB′=∠ACB.
5.解:不能.
6.解:E站应建立在距A站6 km处.理由:因为BF=AB-AE=14-6=8(km),所以AD=BE,AE=BC.在ΔADE和ΔBEC中, 所以ΔADE≌ΔBEC(SAS).所以DE=EC
7.解:由题意并结合图形可以知道BC=CD,∠ACB=∠ECD,又AB∥DE,从而∠A=∠E或∠ABC=∠EDC,故在ΔABC与ΔEDC中,所以ΔABC≌ΔEDC
(AAS),所以AB=ED,即测出ED的长后即可知道A,B之间的距离.
《4.5 利用三角形全等测距离》同步练习2
1,如图,O为AC,BD的中点,则图中全等三角形共有( )对.
A.2 B.3 C.4 D.5
2,如图,AB=AD,AC=AE,∠BAD=∠CAE,那么△ACD≌△AEB的依据是( )
A. ASA B.AAS C.SAS D.SSS
第1题图 第2题图
3,如右图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D.使BC=CD,过D作DE⊥BF,且A,C,E三点在一直线上,若测得DE=15米,即可知道AB也为15米,请你说明理由.
4,要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则次工件的外径必是CD之长了,你能说明其中的道理吗?
5,如图,为修公路,需测量出被大石头阻挡的∠BAC的大小,为此,小张师傅便在直线AC上取点D使AC=CD,在BC的延长线上取点E,使BC=CE,连DE,则只要测出∠D的度数,则知∠A的度数也与∠D的度数相同了,请说明理由.
6,有一座锥形小山,如图,要测量锥形两端A,B的距离,先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A,B的距离,你能说说其中的道理吗?
7,如图所示,要测量湖中小岛E距岸边A和D的距离,作法如下:(1)任作线段AB,取中点0;(2)连接DO并延长使DO=CO;(3)连接BC;(4)用仪器测量E,0在一条线上,并交CB于点F,要测量AE,DE,只须测量BF,CF即可,为什么?
8,如图,沿AC方向开山修路,为了加快施工进度,要在山的另一边同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD,延长,使DF=BD,过F点作AB的平行线MF,连接MD,并延长,在延长线上取一点E,使DE=DM,在E点开工就能使A,C,E成一条直线,你知道其中道理吗?
参考答案
1,C 2,C
3,由题意可知,∠ABC=∠EDC=90o,BC=CD,∠BCA=∠DCE,从而△ABC≌△EDC,故AB=DE=15米
4,显然由OA=OD,OB=OC,∠AOB=∠DOC,可知△AOB≌△COD,从而AB=CD.
5,易知△ABC≌△DEC,故∠A=∠D
6,由条件可知△ABC≌△DCE,故AB=DE
7,由条件可知,△AOD≌△BOC,∴BC=AD,又∠A=∠B,∠AOE=∠BOF,BO=AO,故三角形△AOE≌△BOF,∴BF=AE,从而DE=CF,因此只要测出BF,CF即可知AE,DE的长度了.
8,因为BD=DF,DE=DM,∠BDE=∠MDF,所以△BDE≌△FDM,故∠BEM=∠M,因此BE∥MF,又因为AB∥NF,根据过直线外一点有且只有一条直线与已知直线平行,故A,C,E在一条直线上.
《4.5 利用三角形全等测距离》同步练习3
1.如图,为了要测量湖宽AB,先在AB的延长线上选下C点,再选一适当的点M,然后延长BM、CM到,使,又在的延长线上找一点,使、M、A三点在同一条直线上,这时,只要量出线段的长度就可知湖宽.
你能说明其中的道理吗?
2.如图,将两根钢条的中点O连在一起,可以作成一个测量工件内槽宽的工具(工人把这种工具叫卡钳),只要量出的长度,就可以知道工件的内径AB是否符合标准,你能说出工人这样做的道理吗?
3.如图,有一湖的湖岸在A、B之间呈一段弧状,A、B之间的距离不能直接测量,你能用已学过的知识或方法设计测量方案,求出A、B之间的距离吗?
参考答案
1.提示:≌,≌≌.
2.在和中
∴≌(SAS)
∴
3.方案:在湖右边的空地上选一个能直接到达A点和B点的C点,连接AC并延长至D,使,连接BC并延长至E,使,连接DE,并测量DE的长度即可求出A、B之间的距离.
1.如图5—107所示,将两根钢条AA′,BB′的中点连在一起,使AA′,BB′可以绕着点O自由转动,就做成了一个测量工件,则A′B′的长等于内槽宽AB,那么判定ΔOAB≌ΔOA≌B≌的理由是 ( )
A.边角边 B.角边角 C.边边边 D.角角边
2.如图5—108所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离.你能说明其中的道理吗?
3.如图5—109所示,有一块巨大的长方形广告牌,上面画了一条对角线AC,为了求出这个广告牌的高BC,几个同学在地面上画出了ΔABC,(如图5—110所示),其中∠BAC′=∠BAC,∠ABC′是直角,则BC′的长和广告牌的高是相同的,你能说明其中的道理吗?
4.如图5—111所示,为了测得河宽AB,在地面上作出了与AB垂直的线段AC,又作出了BA的延长线AM,为了在AM上得到与BA相等的线段AB′,还应该怎样做呢?
5.有一个小水库,水面的形状如图5—112所示.能不能仿照课本中的 “想一想”测出
它的最窄的地方A,B两点之间的距离呢?如果能的话,请画图表示出做法.
6.如图5—113所示,铁路上A,B两站(视为直线上两点)相距14 km,C,D为两村 (可视为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=8 km,CB=6 km,现在要在铁路上建一个土特产品收购站E,使C,D两村到正站的距离相等,则E站应 建在距A站多少千米处?
7.如图5—114所示,A,B两个建筑物分别位于河的两岸,要测得它们之间的距离,
可以从B出发沿河岸画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E,C,A在同一条直线卜,则DE的长就等于A,B之间的距离,请你说明道理.
参考答案
1.A[提示:因为O是AA′和BB′的中点,所以OA=OA′,OB=OB′,且∠AOB=∠A′O B′,符合三角形全等的条件.故选A.]
2.解:因为CD=BC,∠ACD=∠ACB=90°,AC=AC,所以ΔACD≌ΔACB,所以AD=AB.
3.提示:由∠CAB=∠C′AB,AB=AB,∠ABC=∠ABC′知,ΔABC与ΔABC′符合“ASA”,且BC与BC′是对应边,所以BC=BC′.
4.提示:在地面上画射线CB′,与AM相交于B′,使∠ACB′=∠ACB.
5.解:不能.
6.解:E站应建立在距A站6 km处.理由:因为BF=AB-AE=14-6=8(km),所以AD=BE,AE=BC.在ΔADE和ΔBEC中, 所以ΔADE≌ΔBEC(SAS).所以DE=EC
7.解:由题意并结合图形可以知道BC=CD,∠ACB=∠ECD,又AB∥DE,从而∠A=∠E或∠ABC=∠EDC,故在ΔABC与ΔEDC中,所以ΔABC≌ΔEDC
(AAS),所以AB=ED,即测出ED的长后即可知道A,B之间的距离.
《4.5 利用三角形全等测距离》同步练习2
1,如图,O为AC,BD的中点,则图中全等三角形共有( )对.
A.2 B.3 C.4 D.5
2,如图,AB=AD,AC=AE,∠BAD=∠CAE,那么△ACD≌△AEB的依据是( )
A. ASA B.AAS C.SAS D.SSS
第1题图 第2题图
3,如右图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D.使BC=CD,过D作DE⊥BF,且A,C,E三点在一直线上,若测得DE=15米,即可知道AB也为15米,请你说明理由.
4,要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则次工件的外径必是CD之长了,你能说明其中的道理吗?
5,如图,为修公路,需测量出被大石头阻挡的∠BAC的大小,为此,小张师傅便在直线AC上取点D使AC=CD,在BC的延长线上取点E,使BC=CE,连DE,则只要测出∠D的度数,则知∠A的度数也与∠D的度数相同了,请说明理由.
6,有一座锥形小山,如图,要测量锥形两端A,B的距离,先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A,B的距离,你能说说其中的道理吗?
7,如图所示,要测量湖中小岛E距岸边A和D的距离,作法如下:(1)任作线段AB,取中点0;(2)连接DO并延长使DO=CO;(3)连接BC;(4)用仪器测量E,0在一条线上,并交CB于点F,要测量AE,DE,只须测量BF,CF即可,为什么?
8,如图,沿AC方向开山修路,为了加快施工进度,要在山的另一边同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD,延长,使DF=BD,过F点作AB的平行线MF,连接MD,并延长,在延长线上取一点E,使DE=DM,在E点开工就能使A,C,E成一条直线,你知道其中道理吗?
参考答案
1,C 2,C
3,由题意可知,∠ABC=∠EDC=90o,BC=CD,∠BCA=∠DCE,从而△ABC≌△EDC,故AB=DE=15米
4,显然由OA=OD,OB=OC,∠AOB=∠DOC,可知△AOB≌△COD,从而AB=CD.
5,易知△ABC≌△DEC,故∠A=∠D
6,由条件可知△ABC≌△DCE,故AB=DE
7,由条件可知,△AOD≌△BOC,∴BC=AD,又∠A=∠B,∠AOE=∠BOF,BO=AO,故三角形△AOE≌△BOF,∴BF=AE,从而DE=CF,因此只要测出BF,CF即可知AE,DE的长度了.
8,因为BD=DF,DE=DM,∠BDE=∠MDF,所以△BDE≌△FDM,故∠BEM=∠M,因此BE∥MF,又因为AB∥NF,根据过直线外一点有且只有一条直线与已知直线平行,故A,C,E在一条直线上.
《4.5 利用三角形全等测距离》同步练习3
1.如图,为了要测量湖宽AB,先在AB的延长线上选下C点,再选一适当的点M,然后延长BM、CM到,使,又在的延长线上找一点,使、M、A三点在同一条直线上,这时,只要量出线段的长度就可知湖宽.
你能说明其中的道理吗?
2.如图,将两根钢条的中点O连在一起,可以作成一个测量工件内槽宽的工具(工人把这种工具叫卡钳),只要量出的长度,就可以知道工件的内径AB是否符合标准,你能说出工人这样做的道理吗?
3.如图,有一湖的湖岸在A、B之间呈一段弧状,A、B之间的距离不能直接测量,你能用已学过的知识或方法设计测量方案,求出A、B之间的距离吗?
参考答案
1.提示:≌,≌≌.
2.在和中
∴≌(SAS)
∴
3.方案:在湖右边的空地上选一个能直接到达A点和B点的C点,连接AC并延长至D,使,连接BC并延长至E,使,连接DE,并测量DE的长度即可求出A、B之间的距离.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
