江苏省常州市教育学会2018-2019学年第二学期学生学业水平监测高一数学2019.6
文档属性
| 名称 | 江苏省常州市教育学会2018-2019学年第二学期学生学业水平监测高一数学2019.6 |

|
|
| 格式 | zip | ||
| 文件大小 | 871.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-19 10:26:32 | ||
图片预览




文档简介
常州市教育学会学生学业水平监测
高一数学试题
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.掷一枚质地均匀的硬币,连续出现5次正面向上,则第6次出现反面向上的概率( )
A.大于 B.等于
C.小于 D.以上都有可能
2.某校高一、高二、高三年级的学生人数之比为6:5:4,现按年级用分层抽样的方法抽取若干人,若抽取的高一年级的学生数为18,则抽取的样本容量为( )
A.45 B.15 C.12 D.27
3.在平面直角坐标系中,过点(2,0)且斜率为﹣1的直线不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.直线x+y﹣1=0的倾斜角为( )
A. B. C. D.
5.在△ABC中,已知sin A:sin B:sinC=2:3:4,那么△ABC最小内角的余弦值为( )
A. B. C. D.
6.已知圆锥的高和底面半径都为1,则其侧面积为( )
A. B.π C. D.()π
7.已知一个正四棱锥的所有棱长都为1,则此四棱锥的体积为( )
A. B. C. D.
8.平行直线ax+2y﹣3=0和2x+ay+1﹣2a=0之间的距离为( )
A. B.2 C.2 D.
9.已知m,n是两条不同的直线,α,β是两个不同的平面.
①若m?α,m⊥β,则α⊥β;
②m?α,α∩β=n,α⊥β,则m⊥n;
③若m?α,n?β,α∥β,则m∥n;
④m∥α,m?β,α∩β=n,则m∥n.
上述说法中,正确的个数为( )
A.1 B.2 C.3 D.4
10.如图,四棱锥S﹣ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中,错误的是( )
A.AC⊥SB
B.BC∥平面SAD
C.SA和SC与平面SBD所成的角相等
D.异面直线AB与SC所成的角和异面直线CD与SA所成的角相等
11.在△ABC中,角A,B,C所对的边分别为a,b,c,若a﹣b=ccosB﹣ccosA,则△ABC的形状为( )
A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰三角形或直角三角形
12.在平面直角坐标系xOy中,直线l1:kx﹣y+4=0与直线l2:x+ky﹣3=0相交于点P,则当实数k变化时,点P到直线4x﹣3y+10=0的距离的最大值为( )
A.2 B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
13.已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是 .
14.在△ABC中,角A,B,C所对的边分别为a,b,c,已知5a=8b,A=2B,则sinB= .
15.已知直线l过点(1,0)且与直线x+y﹣1=0垂直,l与圆C:(x﹣6)2+(y)2=12交于A,B两点,则弦AB的长为 .
16.在平面直角坐标系xOy中,已知直线l:y=x+m和圆C:(x﹣2)2+(y﹣1)2=4.若直线l上存在点P,使?0,则实数m的取值范围是 .
三、解答题(本大题共6小题,共70分。解答时应写出文字说明、证明过程或演算步骤.)
17.如图,在平面四边形ABCD中,BC=3,CD=5,DA,A,∠DBA.
(1)求BD的长:
(2)求△BCD的面积.
18.箱子中有形状、大小都相同的3只红球,2只白球,从中一次摸出2只球.
(1)求摸到的2只球颜色不同的概率:
(2)求摸到的2只球中至少有1只红球的概率.
19.如图,四边形ABCD为矩形,平面ABCD⊥平面ABE,F为CE的中点,且AE⊥BE.
(1)求证:AE∥平面BFD:
(2)求证:BF⊥AE.
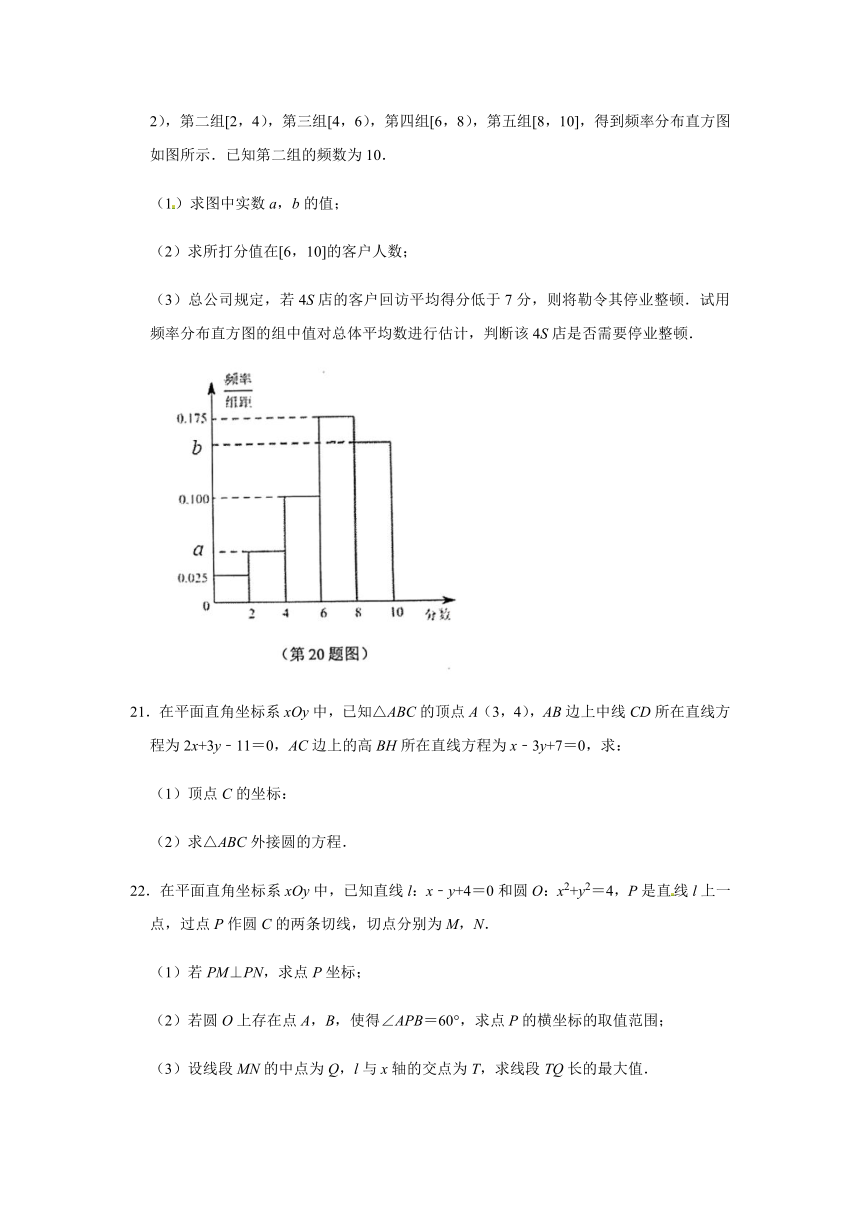
20.今年4月的“西安奔驰女车主哭诉维权事件”引起了社会的广泛关注,某汽车4S店为了调研公司的售后服务态度,对5月份到店维修保养的100位客户进行了回访调查,每位客户用10分制对该店的售后服务进行打分.现将打分的情况分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到频率分布直方图如图所示.已知第二组的频数为10.
(1)求图中实数a,b的值;
(2)求所打分值在[6,10]的客户人数;
(3)总公司规定,若4S店的客户回访平均得分低于7分,则将勒令其停业整顿.试用频率分布直方图的组中值对总体平均数进行估计,判断该4S店是否需要停业整顿.
21.在平面直角坐标系xOy中,已知△ABC的顶点A(3,4),AB边上中线CD所在直线方程为2x+3y﹣11=0,AC边上的高BH所在直线方程为x﹣3y+7=0,求:
(1)顶点C的坐标:
(2)求△ABC外接圆的方程.
22.在平面直角坐标系xOy中,已知直线l:x﹣y+4=0和圆O:x2+y2=4,P是直线l上一点,过点P作圆C的两条切线,切点分别为M,N.
(1)若PM⊥PN,求点P坐标;
(2)若圆O上存在点A,B,使得∠APB=60°,求点P的横坐标的取值范围;
(3)设线段MN的中点为Q,l与x轴的交点为T,求线段TQ长的最大值.
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.B
2.A
3.C
4.C
5.C
6.A
7.C
8.A
9.B
10.D
11.D
12.B
二、填空题(本大题共4小题,每小题5分,满分20分)
13. 0.1.
14.
15. 6.
16.圆C:(x﹣2)2+(y﹣1)2=4的圆心C(2,1),
设P(x,x+m),
?0即为(﹣x,﹣x﹣m)?(2﹣x,1﹣x﹣m)≤0,
可得x2﹣2x﹣x﹣m+(x+m)2≤0,
化为2x2﹣(3﹣2m)x+m2﹣m≤0,
由题意可得△≥0,即(3﹣2m)2﹣8(m2﹣m)≥0,
化为4m2+4m﹣9≤0,
解得m.
三、解答题(本大题共6小题,共70分。解答时应写出文字说明、证明过程或演算步骤.)
17.(1)在△ABD中,DA,A,∠DBA.
可得,
即有BD7;
(2)在△BCD中,BC=3,DC=5,BD=7,
可得cosC,
sinC,
可得△BCD的面积为SBC?DC?sinC3×5.
18.(1)箱子中有形状、大小都相同的3只红球,2只白球,从中一次摸出2只球.
基本事件总数n10,
摸到的2只球颜色不同包含的基本事件个数m6,
∴摸到的2只球颜色不同的概率p.
(2)摸到的2只球中至少有1只红球包含的基本事件个数m′9,
∴摸到的2只球中至少有1只红球的概率p.
19.证明:(1)以E为原点,EB为x轴,EA为y轴,过E作平面ABE的垂线为z轴,建立空间直角坐标系,
设BE=a,AE=b,AD=c,
则A(0,b,0),E(0,0,0),F(),B(a,0,0),D(0,b,c),
(0,﹣b,0),(,0,),(﹣a,b,c),
设平面BDF的法向量(x,y,z),
则,取x=c,得(c,0,a),
∵AE?平面BDE,0,
∴AE∥平面BFD.
(2)∵(0,﹣b,0),(,0,),
∴?0,
∴BF⊥AE.
20.(1)由题意得:,
解得a=0.05,b=0.15.
(2)所打分值在[6,10]的频率为(0.175+0.15)×2=0.65,
∴所打分值在[6,10]的客户人数为:0.65×100=65.
(3)由题意得该4S店平均分为:
1×0.025×2+3×0.05×2+5×0.1×2+7×0.175×2+9×0.15×2=6.5,
∵6.5<7,
∴该4S店需要停业整顿.
21.(1)∵AC⊥BH,BH的方程为x﹣3y+7=0,不妨设直线AC的方程为3x+y+m=0,
将A(3,4)代入得9+4+m=0,解得m=﹣13,
∴直线AC的方程为3x+y﹣13=0,
联立直线AC,CD的方程,即,
解得点C的坐标为(4,1);
(2)设B(x0,y0),则D(,),
∵点B在BH上,点D在CD上,
∴,解得B(﹣1,2),
设△ABC外接圆的方程为x2+y2+Dx+Ey+F=0.
∴,解得,E,F.
∴△ABC外接圆的方程为7x2+7y2﹣22x﹣26y﹣5=0.
22.(1)若PM⊥PN,则四边形PMON为正方形,
则P到圆心的距离为,
∵P在直线x﹣y+4=0上,设P(x,x+4)
故|OP|,解得x=﹣2,
故P(﹣2,2);
(2)设P(x,x+4),若圆O上存在点A,B,使得∠APB=60°,
过P作圆的切线PC,PD,∴∠CPD≥600,∴∠CPO≥300,
在直角三角形△CPO中,∵300≤∠CPO<900,∴sin∠CPO<1,
即1,∴2<OP≤4,
∴24,解得﹣4≤x≤0,
∴点P的横坐标的取值范围为:[﹣4,0];
(3)设P(x0,x0+4),则以OP为直径的圆的方程为,
化简得,与x2+y2=4联立,
可得MN所在直线方程:x0x+(x0+4)y=4,
联立,得,
∴Q的坐标为(,),
可得:Q点的轨迹为:,圆心C(,),半径R.其中原点(0,0)为极限点(也可以去掉).
由题可知T(﹣4,0),∴|TC|.
∴|TQ|≤|TC|+R=3.
∴线段TQ长的最大值为3.
