人教版高中物理必修二教案:6.1圆周运动word版含答案
文档属性
| 名称 | 人教版高中物理必修二教案:6.1圆周运动word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 136.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-17 09:29:12 | ||
图片预览




文档简介
课 时 教 案
第 六 单元 第 1 案 总第 案
课题: §6.1 圆周运动 2020年 月 日
教学目标 核心素养
物理观念:知道什么是圆周运动、匀速圆周运动 及运动特点
物理观念:理解线速度、角速度、周期、转速等概念并会定量计算
科学思维:掌握线速度、角速度与周期之间的关系并会解决问题
科学思维:掌握常见传动装置的特点
教学重点
1.匀速圆周运动 及运动特点
2.线速度、角速度、周期、转速等概念及定量计算
3. 线速度、角速度与周期之间的关系及常见传动装置的特点
教学难点
1. 线速度、角速度、周期、转速等概念及定量计算
2. 线速度、角速度与周期之间的关系及常见传动装置的特点
高考考点
课 型
新授
教 具
教 法
教 学 过 程
教学环节
教师活动预设
学生活动预设
复习引入:
1.为什么有的物体做直线运动,有的物体做曲线运动。
2.平抛运动的受力特点及运动特点?
在日常生活中我们经常会见到另外一种运动:圆周运动。它有哪些性质呢?本章我们就来探索圆周运动的规律及这些规律在生活和科技中的应用。
一、圆周运动
观察游乐场摩天轮、钟表指针的尖端、电风扇叶片上的某一点,发现这些点的运动轨迹是一个圆。
1.定义:运动轨迹为圆周或一段圆弧的机械运动,是一种常见的曲线运动。
阅读课本P22内容,回答相关问题。
1.什么是曲线运动
2.举例
3.怎样描述?
教学环节
教师活动预设
学生活动预设
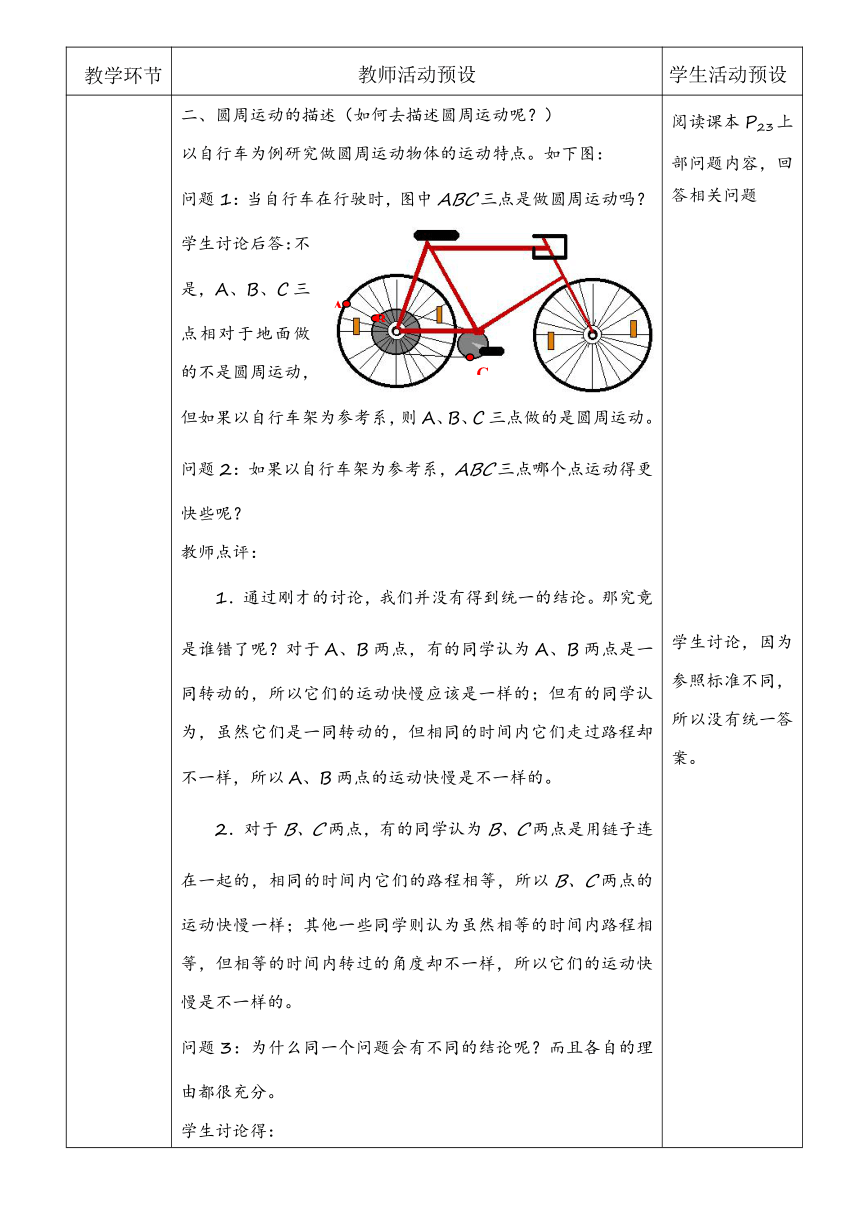
二、圆周运动的描述(如何去描述圆周运动呢?)
以自行车为例研究做圆周运动物体的运动特点。如下图:
问题1:当自行车在行驶时,图中ABC三点是做圆周运动吗?
学生讨论后答:不是,A、B、C三点相对于地面做的不是圆周运动,但如果以自行车架为参考系,则A、B、C三点做的是圆周运动。
问题2:如果以自行车架为参考系,ABC三点哪个点运动得更快些呢?
教师点评:
1.通过刚才的讨论,我们并没有得到统一的结论。那究竟是谁错了呢?对于A、B两点,有的同学认为A、B两点是一同转动的,所以它们的运动快慢应该是一样的;但有的同学认为,虽然它们是一同转动的,但相同的时间内它们走过路程却不一样,所以A、B两点的运动快慢是不一样的。
2.对于B、C两点,有的同学认为B、C两点是用链子连在一起的,相同的时间内它们的路程相等,所以B、C两点的运动快慢一样;其他一些同学则认为虽然相等的时间内路程相等,但相等的时间内转过的角度却不一样,所以它们的运动快慢是不一样的。
问题3:为什么同一个问题会有不同的结论呢?而且各自的理由都很充分。
学生讨论得:
好像是我们衡量的标准不同,对于AB的运动,如果从角度方面考虑,AB的运动就是一样的,如果从转过的路程方面来
阅读课本P23上部问题内容,回答相关问题
学生讨论,因为参照标准不同,所以没有统一答案。
教学环节
教师活动预设
学生活动预设
考虑,AB的运动就不一样了。
教师总结:
要完整地描述物体的圆周运动的快慢,仅仅从角度方面或仅仅从路程方面来考虑都是不全面的,必须综合以上两个方面共同考虑。
下面我们先考虑如何从路程方面来研究圆周运动的快慢。因为物体做圆周运动的路程就对应于圆上的弧长,所以我们需要研究的就是弧长随时间的变化快慢。
如上图中的AB两点,虽然它们相等的时间内转过的角度相同,但它们转过的弧长却不相同,为了描述AB在运动过程中弧长变化快慢的不同,物理学中引入一个量来描述它。这个量叫做“线速度”,用符号v表示。
1.线速度
我们是从两个方面考虑物体做圆周运动的快慢,为了区分,我们把从弧长方面考虑得到的速度叫做“线速度”,把从角度方面考虑得到的速度叫做“角速度”。
①.定义:做圆周运动的物体某段时间内的弧长与该段时间的比值叫做线速度。定义式:
②.物理意义:描述做圆周运动的物体运动快慢的物理量
③.单位:米每秒 符号:m/s
线速度也有平均线速度与瞬时线速度之分。如果时间间隔t取得很小很小,那得到的平均线速度就可以代表瞬时线速度。
问题:在这里为什么不用速度这个概念来描述物体运动的快慢,反而引入一个新的物理量线速度呢?
举例说明:分别用线速度和速度来描述这个运动的快慢,如右图,两物体同时从A点出发,沿顺时针做圆周运动,经过时
间t,甲到了B点,乙到C点,均未走完一圈,则:
学生区分两种不同的描述方式,一种从转过的弧长,一种从转过的角度。
注意强调:线速度是相对圆心的速度。
教学环节
教师活动预设
学生活动预设
①甲乙谁的平均线速度大? 甲<乙
②甲乙谁的平均速度大? 甲>乙
结论:用平均速度无法准确描述做圆周运动的物体的运动快慢。
辨析:瞬时线速度大小与瞬时速度大小的关系
瞬时线速度是t→0时 的极限值。瞬时速度是t→0时 的极限值。通过作图我们可以看到,当时间t越小时,弧长与位移(弦长)的大小差距越小。当t足够小时,它们的大小几乎没有差别。所以当t→0时,瞬时线速度的大小与瞬时速度的大小相等
结论:瞬时线速度的大小与瞬时速度的大小相等
④.方向
线速度是矢量,方向是圆上该点的切线方向。
问题:自行车图中的BC两点,因为它们是用链子连起来的,相同的时间内弧长相等,即线速度大小相等。那它们是完全一样的圆周运动吗?
学生思考后答:不是。
教师分析原因:虽然它们相等的时间内弧长相等,但相等的时间内它们转过的角度却不一样。所以我们还得从角度方面来考虑圆周运动的快慢。
为了描述BC在运动过程中角度变化快慢的不同,物理学中引入一个量来描述它。我们把这个量叫做“角速度”,用符号ω表示。
2.角速度
①.定义:做圆周运动的物体某段时间内转过的角与该段时间的比值叫做角速度。定义式:
②.物理意义:描述做圆周运动的物体转动快慢的物理量
通过做图让学生体会二者之间的关系。
学生再次阅读课本P23图6.1-1,体会当t→0时AB两点重合,割线变成了切线,得出线速度方向
教学环节
教师活动预设
学生活动预设
③.单位:rad/s或 s-1
弧度的定义:
那弧度是个怎样的单位呢?
我们知道,同样半径的圆,圆心角θ越大,它所对的圆弧的弧长就越大,二者成正比。,因此可以用弧长与半径的比值表示角的大小。公式
从表达式分析θ的单位,为了表达的方便,把弧长与半径的比值常数与普通常数区分开来,我们给θ一个单位“弧度”,用符号rad表示。
问题:那弧度与我们平时熟知的角度是如何换算的呢?比如180°对应的弧度是多少呢?
注意:弧度不是通常意义上的单位,单位计算时,不要把“rad”带到公式中计算,弧度的真实单位是1,角速度的真实单位是。
④.方向: 四指绕着转动方向抓,大拇指指向就是角速度方向。(角速度方向与转向有关,转向不变,角速度方向就不变)
3.周期
物体做圆周运动时,每隔一段时间就要重复一次原来的运动,我们把这样的运动称为周期性运动。同学们能不能举出一些日常生活中常见的周期性运动。
学生举例:在周期性运动中每完成一次周期性运动所需要的时间叫做周期T。如地球自转周期是一天,公转周期是一年。
①.定义:周期性运动每重复一次所需要的时间叫做周期T。
②.单位:秒 s
4.频率:频率描述周期性运动还常用到频率的概念。
①.定义:单位时间内周期性运动的次数。用f表示
学生阅读课本P24中部内容,体会角速度单位的定义方法
学生分析:圆的周长公式为,所对应的圆心角是360°,所以由 得出角度对应的弧度。依次类推
教学环节
教师活动预设
学生活动预设
②.与周期的关系:
③.单位:s-1
5、转速
技术中常用转速来描述转动物体上质点做圆周运动的快慢。
①.定义:转速是指物体单位时间内转过的圈数,用符号n表示。
②.常用单位:转每秒 r/s 转每分 r/min
注意:转速不是国际单位制单位,运算时往往要把它们换算成弧度每秒。
三、匀速圆周运动
教师分析:你知道什么是匀速圆周运动吗?你能分别用线速度和角速度来描述匀速圆周运动的特点吗?
1.定义:线速度大小不变(或角速度不变)的圆周运动
问题:匀速圆周运动是匀速运动吗?
总结:不是。“匀速”指的是匀速率,即线速度大小不变。线速度方向一直在变,所以匀速圆周运动是变速运动。
2.运动性质:匀速圆周运动是变速运动。
理解:匀速圆周运动是一种理想化的运动形式。但由于现实中
许多物体的运动接近这种运动,所以匀速圆周运动这种模型又具有一定的实际意义。一般圆周运动,也可以取一段较短的时间(或弧长)看成是匀速圆周运动.
四、各物理量间的关系
1.线速度与角速度的关系:
2.线速度与T的关系、角速度与T的关系:
学生思考回答:匀速圆周运动就是指物体均匀转动,线速度处处大小相等,角速度不变。
明确变量和不变量(T、f、n不变,转动方向时刻变)
引导学生推导
注意适用条件(匀速圆周运动)
教学环节
教师活动预设
学生活动预设
3.线速度与转速的关系、角速度与转速的关系
例1、分析下面两个图中ABC三点的关系。
例2.关于匀速圆周运动,下列说法正确的是(AC)
A.任意相等时间内物体通过的路程相等。
B.任意相等时间内物体通过的位移相等
C.任意相等时间内物体半径扫过的弧度相等
D.匀速圆周运动是匀速运动
例3.如图所示,两个皮带轮通过皮带传动(皮带不打滑),大轮半径是小轮半径的2倍,则两轮边缘上A、B两点的线速度,角速度、周期和频率的关系为;;
[解答]1:1 1:2 2:1 1:2
例4.地球上北纬30度和北纬60度上各有一点A和B,则它们之间的角速度和线速度大小之比多少?
【解析】:AB两点角速度相同,半径之比为,
所以线速度之比为
小结:
第 六 单元 第 1 案 总第 案
课题: §6.1 圆周运动 2020年 月 日
教学目标 核心素养
物理观念:知道什么是圆周运动、匀速圆周运动 及运动特点
物理观念:理解线速度、角速度、周期、转速等概念并会定量计算
科学思维:掌握线速度、角速度与周期之间的关系并会解决问题
科学思维:掌握常见传动装置的特点
教学重点
1.匀速圆周运动 及运动特点
2.线速度、角速度、周期、转速等概念及定量计算
3. 线速度、角速度与周期之间的关系及常见传动装置的特点
教学难点
1. 线速度、角速度、周期、转速等概念及定量计算
2. 线速度、角速度与周期之间的关系及常见传动装置的特点
高考考点
课 型
新授
教 具
教 法
教 学 过 程
教学环节
教师活动预设
学生活动预设
复习引入:
1.为什么有的物体做直线运动,有的物体做曲线运动。
2.平抛运动的受力特点及运动特点?
在日常生活中我们经常会见到另外一种运动:圆周运动。它有哪些性质呢?本章我们就来探索圆周运动的规律及这些规律在生活和科技中的应用。
一、圆周运动
观察游乐场摩天轮、钟表指针的尖端、电风扇叶片上的某一点,发现这些点的运动轨迹是一个圆。
1.定义:运动轨迹为圆周或一段圆弧的机械运动,是一种常见的曲线运动。
阅读课本P22内容,回答相关问题。
1.什么是曲线运动
2.举例
3.怎样描述?
教学环节
教师活动预设
学生活动预设
二、圆周运动的描述(如何去描述圆周运动呢?)
以自行车为例研究做圆周运动物体的运动特点。如下图:
问题1:当自行车在行驶时,图中ABC三点是做圆周运动吗?
学生讨论后答:不是,A、B、C三点相对于地面做的不是圆周运动,但如果以自行车架为参考系,则A、B、C三点做的是圆周运动。
问题2:如果以自行车架为参考系,ABC三点哪个点运动得更快些呢?
教师点评:
1.通过刚才的讨论,我们并没有得到统一的结论。那究竟是谁错了呢?对于A、B两点,有的同学认为A、B两点是一同转动的,所以它们的运动快慢应该是一样的;但有的同学认为,虽然它们是一同转动的,但相同的时间内它们走过路程却不一样,所以A、B两点的运动快慢是不一样的。
2.对于B、C两点,有的同学认为B、C两点是用链子连在一起的,相同的时间内它们的路程相等,所以B、C两点的运动快慢一样;其他一些同学则认为虽然相等的时间内路程相等,但相等的时间内转过的角度却不一样,所以它们的运动快慢是不一样的。
问题3:为什么同一个问题会有不同的结论呢?而且各自的理由都很充分。
学生讨论得:
好像是我们衡量的标准不同,对于AB的运动,如果从角度方面考虑,AB的运动就是一样的,如果从转过的路程方面来
阅读课本P23上部问题内容,回答相关问题
学生讨论,因为参照标准不同,所以没有统一答案。
教学环节
教师活动预设
学生活动预设
考虑,AB的运动就不一样了。
教师总结:
要完整地描述物体的圆周运动的快慢,仅仅从角度方面或仅仅从路程方面来考虑都是不全面的,必须综合以上两个方面共同考虑。
下面我们先考虑如何从路程方面来研究圆周运动的快慢。因为物体做圆周运动的路程就对应于圆上的弧长,所以我们需要研究的就是弧长随时间的变化快慢。
如上图中的AB两点,虽然它们相等的时间内转过的角度相同,但它们转过的弧长却不相同,为了描述AB在运动过程中弧长变化快慢的不同,物理学中引入一个量来描述它。这个量叫做“线速度”,用符号v表示。
1.线速度
我们是从两个方面考虑物体做圆周运动的快慢,为了区分,我们把从弧长方面考虑得到的速度叫做“线速度”,把从角度方面考虑得到的速度叫做“角速度”。
①.定义:做圆周运动的物体某段时间内的弧长与该段时间的比值叫做线速度。定义式:
②.物理意义:描述做圆周运动的物体运动快慢的物理量
③.单位:米每秒 符号:m/s
线速度也有平均线速度与瞬时线速度之分。如果时间间隔t取得很小很小,那得到的平均线速度就可以代表瞬时线速度。
问题:在这里为什么不用速度这个概念来描述物体运动的快慢,反而引入一个新的物理量线速度呢?
举例说明:分别用线速度和速度来描述这个运动的快慢,如右图,两物体同时从A点出发,沿顺时针做圆周运动,经过时
间t,甲到了B点,乙到C点,均未走完一圈,则:
学生区分两种不同的描述方式,一种从转过的弧长,一种从转过的角度。
注意强调:线速度是相对圆心的速度。
教学环节
教师活动预设
学生活动预设
①甲乙谁的平均线速度大? 甲<乙
②甲乙谁的平均速度大? 甲>乙
结论:用平均速度无法准确描述做圆周运动的物体的运动快慢。
辨析:瞬时线速度大小与瞬时速度大小的关系
瞬时线速度是t→0时 的极限值。瞬时速度是t→0时 的极限值。通过作图我们可以看到,当时间t越小时,弧长与位移(弦长)的大小差距越小。当t足够小时,它们的大小几乎没有差别。所以当t→0时,瞬时线速度的大小与瞬时速度的大小相等
结论:瞬时线速度的大小与瞬时速度的大小相等
④.方向
线速度是矢量,方向是圆上该点的切线方向。
问题:自行车图中的BC两点,因为它们是用链子连起来的,相同的时间内弧长相等,即线速度大小相等。那它们是完全一样的圆周运动吗?
学生思考后答:不是。
教师分析原因:虽然它们相等的时间内弧长相等,但相等的时间内它们转过的角度却不一样。所以我们还得从角度方面来考虑圆周运动的快慢。
为了描述BC在运动过程中角度变化快慢的不同,物理学中引入一个量来描述它。我们把这个量叫做“角速度”,用符号ω表示。
2.角速度
①.定义:做圆周运动的物体某段时间内转过的角与该段时间的比值叫做角速度。定义式:
②.物理意义:描述做圆周运动的物体转动快慢的物理量
通过做图让学生体会二者之间的关系。
学生再次阅读课本P23图6.1-1,体会当t→0时AB两点重合,割线变成了切线,得出线速度方向
教学环节
教师活动预设
学生活动预设
③.单位:rad/s或 s-1
弧度的定义:
那弧度是个怎样的单位呢?
我们知道,同样半径的圆,圆心角θ越大,它所对的圆弧的弧长就越大,二者成正比。,因此可以用弧长与半径的比值表示角的大小。公式
从表达式分析θ的单位,为了表达的方便,把弧长与半径的比值常数与普通常数区分开来,我们给θ一个单位“弧度”,用符号rad表示。
问题:那弧度与我们平时熟知的角度是如何换算的呢?比如180°对应的弧度是多少呢?
注意:弧度不是通常意义上的单位,单位计算时,不要把“rad”带到公式中计算,弧度的真实单位是1,角速度的真实单位是。
④.方向: 四指绕着转动方向抓,大拇指指向就是角速度方向。(角速度方向与转向有关,转向不变,角速度方向就不变)
3.周期
物体做圆周运动时,每隔一段时间就要重复一次原来的运动,我们把这样的运动称为周期性运动。同学们能不能举出一些日常生活中常见的周期性运动。
学生举例:在周期性运动中每完成一次周期性运动所需要的时间叫做周期T。如地球自转周期是一天,公转周期是一年。
①.定义:周期性运动每重复一次所需要的时间叫做周期T。
②.单位:秒 s
4.频率:频率描述周期性运动还常用到频率的概念。
①.定义:单位时间内周期性运动的次数。用f表示
学生阅读课本P24中部内容,体会角速度单位的定义方法
学生分析:圆的周长公式为,所对应的圆心角是360°,所以由 得出角度对应的弧度。依次类推
教学环节
教师活动预设
学生活动预设
②.与周期的关系:
③.单位:s-1
5、转速
技术中常用转速来描述转动物体上质点做圆周运动的快慢。
①.定义:转速是指物体单位时间内转过的圈数,用符号n表示。
②.常用单位:转每秒 r/s 转每分 r/min
注意:转速不是国际单位制单位,运算时往往要把它们换算成弧度每秒。
三、匀速圆周运动
教师分析:你知道什么是匀速圆周运动吗?你能分别用线速度和角速度来描述匀速圆周运动的特点吗?
1.定义:线速度大小不变(或角速度不变)的圆周运动
问题:匀速圆周运动是匀速运动吗?
总结:不是。“匀速”指的是匀速率,即线速度大小不变。线速度方向一直在变,所以匀速圆周运动是变速运动。
2.运动性质:匀速圆周运动是变速运动。
理解:匀速圆周运动是一种理想化的运动形式。但由于现实中
许多物体的运动接近这种运动,所以匀速圆周运动这种模型又具有一定的实际意义。一般圆周运动,也可以取一段较短的时间(或弧长)看成是匀速圆周运动.
四、各物理量间的关系
1.线速度与角速度的关系:
2.线速度与T的关系、角速度与T的关系:
学生思考回答:匀速圆周运动就是指物体均匀转动,线速度处处大小相等,角速度不变。
明确变量和不变量(T、f、n不变,转动方向时刻变)
引导学生推导
注意适用条件(匀速圆周运动)
教学环节
教师活动预设
学生活动预设
3.线速度与转速的关系、角速度与转速的关系
例1、分析下面两个图中ABC三点的关系。
例2.关于匀速圆周运动,下列说法正确的是(AC)
A.任意相等时间内物体通过的路程相等。
B.任意相等时间内物体通过的位移相等
C.任意相等时间内物体半径扫过的弧度相等
D.匀速圆周运动是匀速运动
例3.如图所示,两个皮带轮通过皮带传动(皮带不打滑),大轮半径是小轮半径的2倍,则两轮边缘上A、B两点的线速度,角速度、周期和频率的关系为;;
[解答]1:1 1:2 2:1 1:2
例4.地球上北纬30度和北纬60度上各有一点A和B,则它们之间的角速度和线速度大小之比多少?
【解析】:AB两点角速度相同,半径之比为,
所以线速度之比为
小结:
