人教版高中物理必修二教案:5.2.2运动的合成和分解(典例分析)word版含答案
文档属性
| 名称 | 人教版高中物理必修二教案:5.2.2运动的合成和分解(典例分析)word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 30.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-18 15:59:36 | ||
图片预览

文档简介
课 时 教 案
第 五 单元 第 3 案 总第 3 案
课题: §5.2.2 运动的合成与分解(典例分析) 2020年 月 日
教学目标 核心素养
物理观念:知道什么是合运动、分运动,知道合运动与分运动的关系
物理观念:知道运动的合成与分解,理解运动的合成与分解遵循平行四边形定则
科学思维:掌握运动的合成与分解的方法
科学思维:会用作图法和计算法求解位移和速度的合成与分解问题
教学重点
1. 运动的合成与分解的方法
2. 合运动与分运动的关系、特点
3. 运动合成与分解的应用
教学难点
1.如何对运动进行分解
2. 求解位移和速度的合成与分解问题
3.运动模型的运动分解(关联物体)
高考考点
课 型
新授
教 具
教 法
教 学 过 程
教学环节
教师活动预设
学生活动预设
复习引入:
1.曲线运动的条件。(学生答:F与v不共线)
2.什么是合运动、分运动
3.运动的合成、分解的概念
4.怎样确定合运动的性质。(F合与v合的方向关系)
典例分析: 一、小船过河
如图:一条小河宽为d,水流速度v水,船在静水中的速度v船,
小明驾船由码头A出发,想要到达河对岸的码头B,但是他驾船时始终保持船头指向与河岸垂直,如图示,这样小明没有到达正对岸的码头B,而是到达下游的C处。
教学环节
教师活动预设
学生活动预设
⑴此过程中小船参与了哪些运动?
⑵小明驾船渡河的时间与哪个分运动的速度有关?与哪个分运动的速度无关?
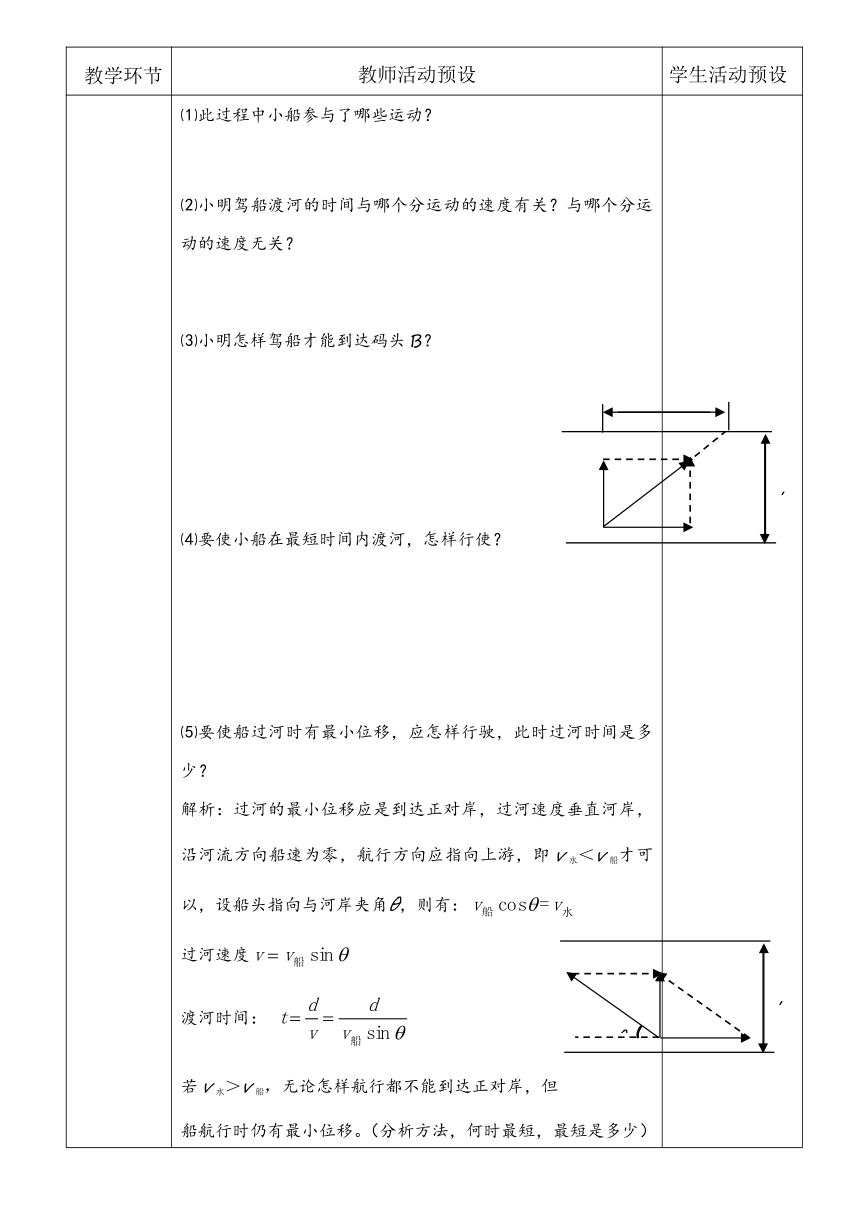
⑶小明怎样驾船才能到达码头B?
⑷要使小船在最短时间内渡河,怎样行使?
⑸要使船过河时有最小位移,应怎样行驶,此时过河时间是多少?
解析:过河的最小位移应是到达正对岸,过河速度垂直河岸,沿河流方向船速为零,航行方向应指向上游,即v水<v船才可以,设船头指向与河岸夹角θ,则有:
过河速度
渡河时间:
若v水>v船,无论怎样航行都不能到达正对岸,但
船航行时仍有最小位移。(分析方法,何时最短,最短是多少)
教学环节
教师活动预设
学生活动预设
例1.河宽L=100m,河中的水流速度u=4m/s,现有一相对静水速度为5m/s的摩托艇渡河。
⑴渡河的最短时间是多少?渡河的最短位移是多少?
⑵若船速v=3m/s,渡河的最短时间和最短位移又是多少?
⑶要使摩托艇到达出发点下游20m的对岸,则船速不得小于多少?
解:(略)
2.汽船顺流从甲地到乙地,历时3h,返回时需6h,如汽船关闭发动机顺流从甲地漂到乙地,则所需时间为多少?
解:设船流v1,水流速度v2,两地距离s,则有:
①
②
由①②两式可得:
设汽船漂流到乙地所用时间为t,可得:
将v1带入上式得:t=4h
二、绳拉物体末端速度的分解
例:如图,通过定滑轮用恒定速率v拉小车,试问:⑴当绳与水平方向成θ角时,小车的运动速度为多大?⑵小车运动过程中做的是加速运动还是减速运动。
教学环节
教师活动预设
学生活动预设
解析:对A点所参与的运动:
①沿绳子方向的运动;②以o点为圆心
的摆动随船水平向左的运动为A点的实际运动。
由几何关系可得(如图):
得:
靠岸过程中,θ增大,减小,车速增大。
变式:
如图:滑块A在水平面上,滑
块B套在竖直杆上向下运动,
A、B通过跨过定滑轮的细绳
连接,当连线与水平方向的夹角
为θ时两个滑块间的速度关系。
解略
第 五 单元 第 3 案 总第 3 案
课题: §5.2.2 运动的合成与分解(典例分析) 2020年 月 日
教学目标 核心素养
物理观念:知道什么是合运动、分运动,知道合运动与分运动的关系
物理观念:知道运动的合成与分解,理解运动的合成与分解遵循平行四边形定则
科学思维:掌握运动的合成与分解的方法
科学思维:会用作图法和计算法求解位移和速度的合成与分解问题
教学重点
1. 运动的合成与分解的方法
2. 合运动与分运动的关系、特点
3. 运动合成与分解的应用
教学难点
1.如何对运动进行分解
2. 求解位移和速度的合成与分解问题
3.运动模型的运动分解(关联物体)
高考考点
课 型
新授
教 具
教 法
教 学 过 程
教学环节
教师活动预设
学生活动预设
复习引入:
1.曲线运动的条件。(学生答:F与v不共线)
2.什么是合运动、分运动
3.运动的合成、分解的概念
4.怎样确定合运动的性质。(F合与v合的方向关系)
典例分析: 一、小船过河
如图:一条小河宽为d,水流速度v水,船在静水中的速度v船,
小明驾船由码头A出发,想要到达河对岸的码头B,但是他驾船时始终保持船头指向与河岸垂直,如图示,这样小明没有到达正对岸的码头B,而是到达下游的C处。
教学环节
教师活动预设
学生活动预设
⑴此过程中小船参与了哪些运动?
⑵小明驾船渡河的时间与哪个分运动的速度有关?与哪个分运动的速度无关?
⑶小明怎样驾船才能到达码头B?
⑷要使小船在最短时间内渡河,怎样行使?
⑸要使船过河时有最小位移,应怎样行驶,此时过河时间是多少?
解析:过河的最小位移应是到达正对岸,过河速度垂直河岸,沿河流方向船速为零,航行方向应指向上游,即v水<v船才可以,设船头指向与河岸夹角θ,则有:
过河速度
渡河时间:
若v水>v船,无论怎样航行都不能到达正对岸,但
船航行时仍有最小位移。(分析方法,何时最短,最短是多少)
教学环节
教师活动预设
学生活动预设
例1.河宽L=100m,河中的水流速度u=4m/s,现有一相对静水速度为5m/s的摩托艇渡河。
⑴渡河的最短时间是多少?渡河的最短位移是多少?
⑵若船速v=3m/s,渡河的最短时间和最短位移又是多少?
⑶要使摩托艇到达出发点下游20m的对岸,则船速不得小于多少?
解:(略)
2.汽船顺流从甲地到乙地,历时3h,返回时需6h,如汽船关闭发动机顺流从甲地漂到乙地,则所需时间为多少?
解:设船流v1,水流速度v2,两地距离s,则有:
①
②
由①②两式可得:
设汽船漂流到乙地所用时间为t,可得:
将v1带入上式得:t=4h
二、绳拉物体末端速度的分解
例:如图,通过定滑轮用恒定速率v拉小车,试问:⑴当绳与水平方向成θ角时,小车的运动速度为多大?⑵小车运动过程中做的是加速运动还是减速运动。
教学环节
教师活动预设
学生活动预设
解析:对A点所参与的运动:
①沿绳子方向的运动;②以o点为圆心
的摆动随船水平向左的运动为A点的实际运动。
由几何关系可得(如图):
得:
靠岸过程中,θ增大,减小,车速增大。
变式:
如图:滑块A在水平面上,滑
块B套在竖直杆上向下运动,
A、B通过跨过定滑轮的细绳
连接,当连线与水平方向的夹角
为θ时两个滑块间的速度关系。
解略
