1.2.2 直角三角形的全等判定课件

(共21张PPT)
数学北师大版

八年级
1.2第2课时直角三角形的全等判定
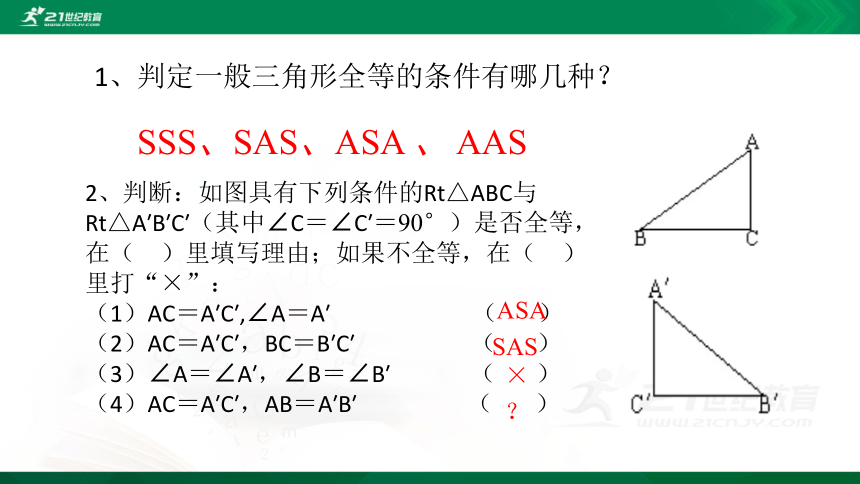
1、判定一般三角形全等的条件有哪几种？
SSS、SAS、ASA 、 AAS
2、判断：如图具有下列条件的Rt△ABC与Rt△A′B′C′（其中∠C＝∠C′＝90°）是否全等，在（　）里填写理由；如果不全等，在（　）里打“×”：
（1）AC＝A′C′,∠A＝A′ （ ）
（2）AC＝A′C′，BC＝B′C′　 （ ）
（3）∠A＝∠A′，∠B＝∠B′ （ ）
（4）AC＝A′C′，AB＝A′B′　 （　 ）
ASA
SAS
×
？
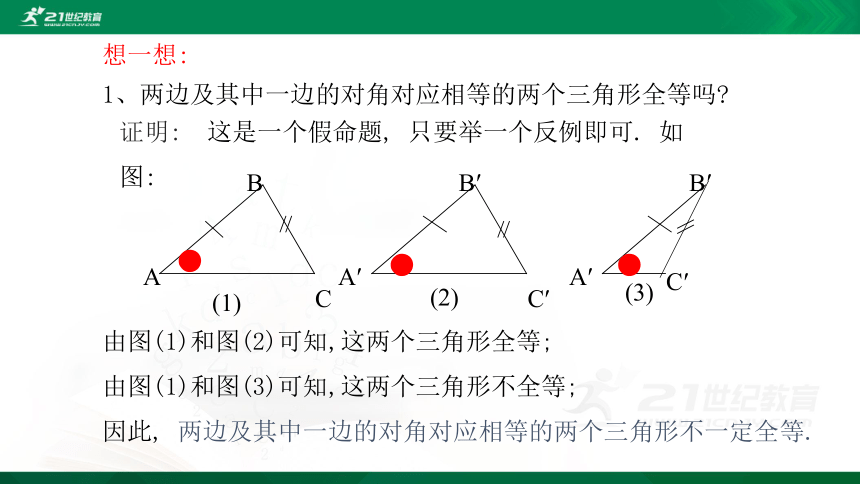
想一想:
1、两边及其中一边的对角对应相等的两个三角形全等吗?
证明: 这是一个假命题, 只要举一个反例即可. 如图:


A
B
C



A′
B′
C′









A′
B′
C′




●
●
●
(1)
(2)
(3)
由图(1)和图(2)可知,这两个三角形全等;
由图(1)和图(3)可知,这两个三角形不全等;
因此, 两边及其中一边的对角对应相等的两个三角形不一定全等.
2、如果其中一组等边的所对的角是直角, 那么这两个三角形全等吗？.
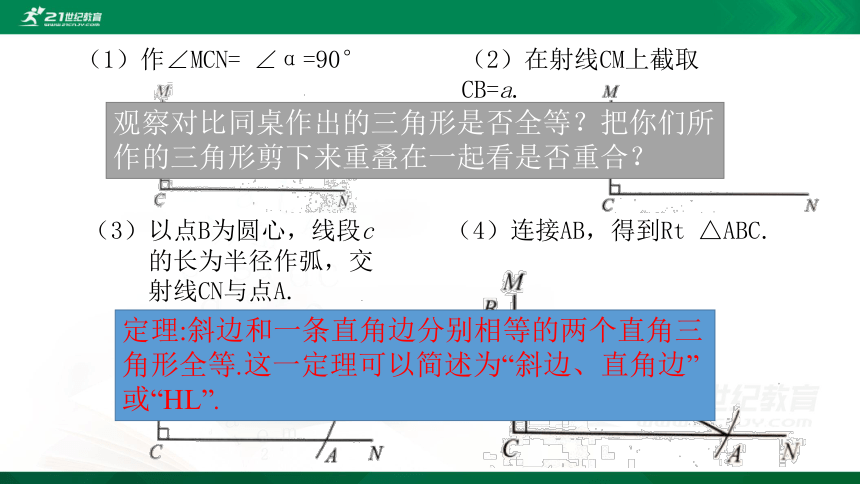
做一做：已知一条直角边和斜边，求作一个直角三角形.
已知：如图，线段a=4cm，c=5cm（a求作：Rt △ABC，使∠C= ∠ α ，BC=a，AB=c.
（1）作∠MCN= ∠α=90°
（2）在射线CM上截取CB=a.
（3）以点B为圆心，线段c
的长为半径作弧，交
射线CN与点A.
（4）连接AB，得到Rt △ABC.
观察对比同桌作出的三角形是否全等？把你们所作的三角形剪下来重叠在一起看是否重合？
定理:斜边和一条直角边分别相等的两个直角三角形全等.这一定理可以简述为“斜边、直角边”或“HL”.
已知：如图, 在△ABC和△A′B′C′中, ∠C=∠C′=90°, AC=A′C ′, AB=A′B′
求证：△ABC≌△A′B′C′ .
证明：在△ABC中，
∵∠C=90°，
∴BC2=AB2-AC2（勾股定理）.
同理，B′C′2=A′B′2-A′C′2 .
∵AB=A′B′，AC=A′C′，
∴BC=B′C′.
∴ △ABC ≌ △A′B′C′（SSS）.

A
B
C



A′
B′
C′


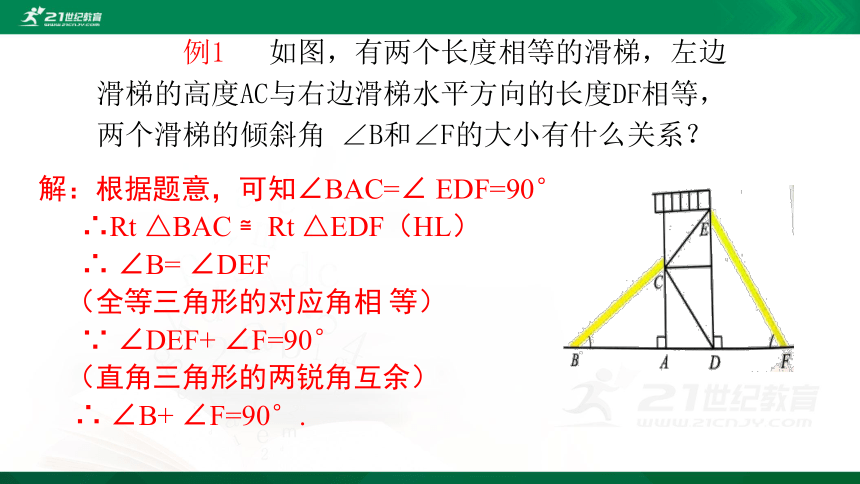
例1 如图，有两个长度相等的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角 ∠B和∠F的大小有什么关系？
解：根据题意，可知∠BAC=∠ EDF=90°
∴Rt △BAC ≌Rt △EDF（HL）
∴ ∠B= ∠DEF
（全等三角形的对应角相 等）
∵ ∠DEF+ ∠F=90°
（直角三角形的两锐角互余）
∴ ∠B+ ∠F=90°.
1. 判断下列命题的真假,并说明理由:
两个锐角对应相等的两个直角三角形全等;
斜边及一个锐角对应相等的两个直角三角形全等;
两直角边对应相等的两个直角三角形全等;
一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.
假
真
真
真
例2　如图所示,在△ABC中,AB=CB,∠ABC=90°,点F为
AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
(1)证明:∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∵AE=CF,AB=BC,
∴Rt△ABE≌Rt△CBF(HL).

(2)解:∵AB=BC,∠ABC=90°,
∴∠CAB=∠ACB=45°.
∵∠BAE=∠CAB-∠CAE=45°-30°=15°.
由(1)知Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°.
∴∠ACF=∠BCF+∠ACB=45°+15°=60°.
拓展点一　利用勾股定理解决图形折叠问题
例3　如图,直角三角形纸片ABC,∠C=90°,AC=6,BC=8,折叠△ABC的一角,使点B与点A重合,展开得折痕DE,求BD的长.
分析:由折叠知△ADE≌△BDE得到AD=BD,在Rt△ACD中,由勾股定理求AD的长.
解:由折叠可知△ADE≌△BDE,AD=BD.
设BD=x,则AD=x,CD=8-x.
在Rt△ACD中,由勾股定理,得
AC2+CD2=AD2,即62+(8-x)2=x2,
例4　如图所示,已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证:CF=DF.
证明:如图,连接AC,AD,在△ABC和△AED中,
∵AB=AE,BC=ED,∠B=∠E,
∴△ABC≌△AED(SAS).
∴AC=AD.∵AF⊥DC,
∴∠AFC=∠AFD=90°.
在Rt△ACF和Rt△ADF中,
AC=AD,AF=AF,
∴Rt△AFC≌Rt△AFD(HL).∴CF=DF.
例5．如图，AC＝DF，BF＝CE，AB⊥BE，DE⊥BE，垂足分别为B，E.求证：AB＝DE.
证明：∵BF＝CE， ∴BF＋CF＝CE＋CF，即BC＝EF. ∵AB⊥BF，DE⊥BE， ∴∠B＝∠E＝90°. ∵在Rt△ABC和Rt△DEF中，
BC＝EF，AC＝DF，
∴Rt△ABC≌Rt△DEF(HL)， ∴AB＝DE.









直角三角形的判定
小结
1.有一个角等于90°的三角形是直角三角形.
2.有两个角互余的三角形是直角三角形.
3.如果三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形.
4.:斜边和一条直角边分别相等的两个直角三角形全等.这一定理可以简述为“斜边、直角边”或“HL”.

1．如图，AD⊥CD于点D，AB＝10，BC＝20，∠A＝∠C＝30°，求∠ABC的度数．
解：如图，延长AB，交CD于点E. ∵AD⊥CD， ∠A＝∠C＝30°， ∴∠AED＝60°， ∴∠CBE＝30°， ∴∠ABC＝180°－∠CBE＝150°.
课后作业






2．如图，已知某开发区有一块四边形的空地ABCD，现计划在空地上种植草皮，经测量∠A＝90°，AB＝30 m，BC＝120 m，CD＝130 m，DA＝40 m，若植草皮的单价为30元/m2，问：将这块空地植满草皮，开发区需要投入多少元？
解：连接BD，∵∠A＝90°，AB＝30 m，DA＝40 m， ∴BD＝50 m.∵BC＝120 m，CD＝130 m，BD＝50 m， ∴BC2＋BD2＝CD2，∴△BCD是直角三角形，











3．如图，已知AD，AF分别是两个钝角△ABC和△ABE的高，如果AD＝AF，AC＝AE.
求证：BC＝BE.
证明：∵AD，AF分别是两个钝角△ABC
和△ABE的高，且AD＝AF，AC＝AE， ∴Rt△ADC≌Rt△AFE(HL)， ∴CD＝EF. ∵AD＝AF，AB＝AB， ∴Rt△ABD≌Rt△ABF(HL)． ∴BD＝BF， ∴BD－CD＝BF－EF，即BC＝BE.








4．如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．
求证：△OAB是等腰三角形．
证明：∵AC⊥BC，BD⊥AD
∴∠D=∠C=90°，
在Rt△ABD和Rt△BAC中，
∴Rt△ABD≌Rt△BAC（HL），
∴∠DBA=∠CAB，
∴OA=OB，
即△OAB是等腰三角形．
另外一种证法：
证明：∵AC⊥BC，BD⊥AD
∴∠D=∠C=90°
在Rt△ABD和Rt△BAC中
AC=BD，AB=BA
∴Rt△ABD≌Rt△BAC（HL）
∴AD=BC，
在△AOD和△BOC中
∠AOD=∠BOC,AD=BC,∠D=C
∴△AOD≌△BOC（AAS），
∴OA=OB，
即△OAB是等腰三角形．
5．如图，有一直角三角形ABC，∠C=90°，AC=10 cm，BC=5 cm，一条线段PQ=AB，P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动，问P点运动到AC上什么位置时△ABC才能和△APQ全等．
解：根据三角形全等的判定方法HL可知：
①当P运动到AP=BC时，
∵∠C=∠QAP=90°，
在Rt△ABC与Rt△QPA中，
AP=BC,PQ=AB
∴Rt△ABC≌Rt△QPA（HL），即AP=BC=5 cm；
②当P运动到与C点重合时，AP=AC，
在Rt△ABC与Rt△QPA中，
AP=AC,PQ=AB
∴Rt△QAP≌Rt△BCA（HL），即AP=AC=10 cm，
∴当点P与点C重合时，△ABC才能和△APQ全等．
综上所述，当P运动到AP=BC、点P与点C重合时，△ABC才能和△APQ全等．

谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php