人教版2020年七年级数学下册:5.1相交线(基础)同步练习(解析版)
文档属性
| 名称 | 人教版2020年七年级数学下册:5.1相交线(基础)同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 680.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-19 00:00:00 | ||
图片预览

文档简介
人教版2020年七年级下册:5.1相交线(基础)同步练习
一.选择题(共38小题)
1.两条直线相交所成的四个角中,下列说法正确的是( )
A.一定有一个锐角 B.一定有一个钝角
C.一定有一个直角 D.一定有一个不是钝角
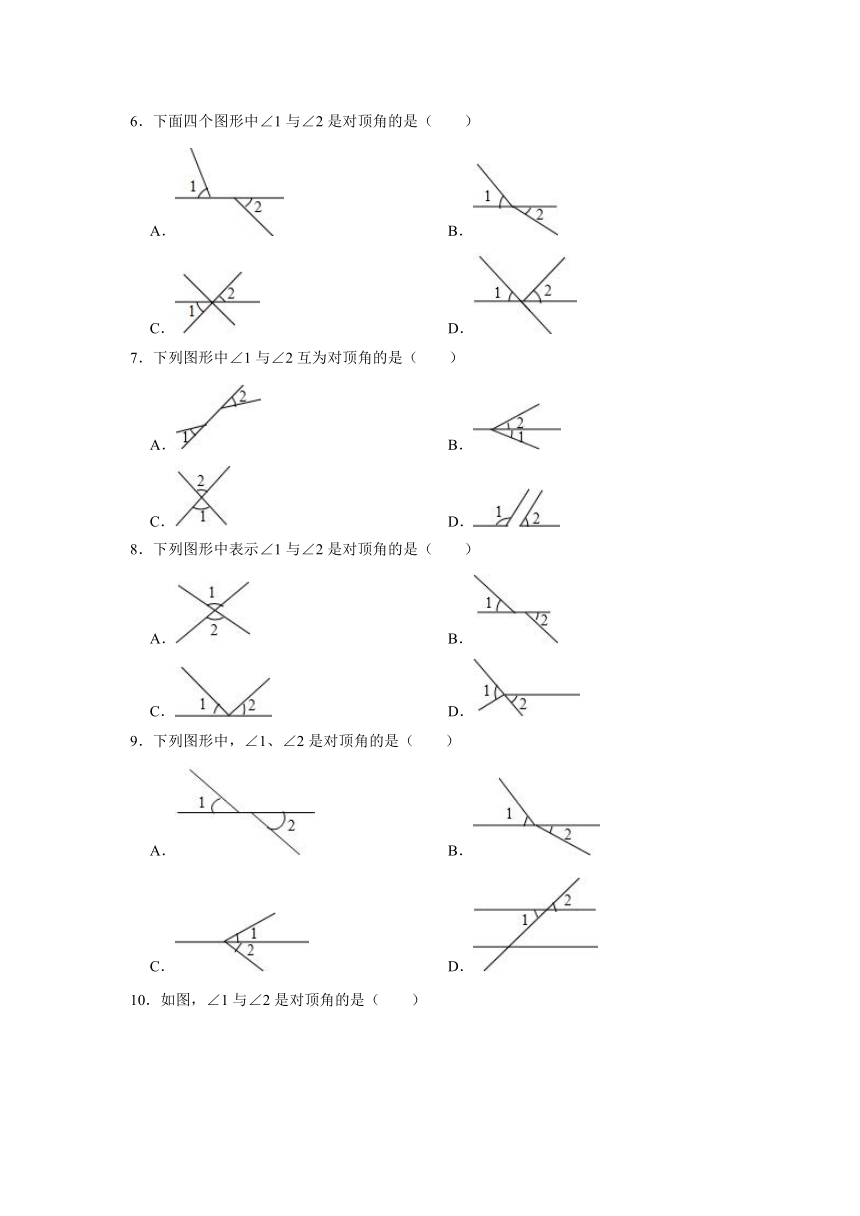
2.下面四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
3.下面四个图形中,∠1与∠2是邻补角的是( )
A. B.
C. D.
4.如图,已知点A,B,N在一条直线上,点F,B,M在一条直线上,点E,F在线段AD上,若∠MBN﹣∠X=∠ABE,则∠X=( )
A.∠EBF B.∠ABE C.∠ABF D.∠EBC
5.下列各组角中,∠1与∠2是对顶角的为( )
A. B.
C. D.
6.下面四个图形中∠1与∠2是对顶角的是( )
A. B.
C. D.
7.下列图形中∠1与∠2互为对顶角的是( )
A. B.
C. D.
8.下列图形中表示∠1与∠2是对顶角的是( )
A. B.
C. D.
9.下列图形中,∠1、∠2是对顶角的是( )
A. B.
C. D.
10.如图,∠1与∠2是对顶角的是( )
A. B.
C. D.
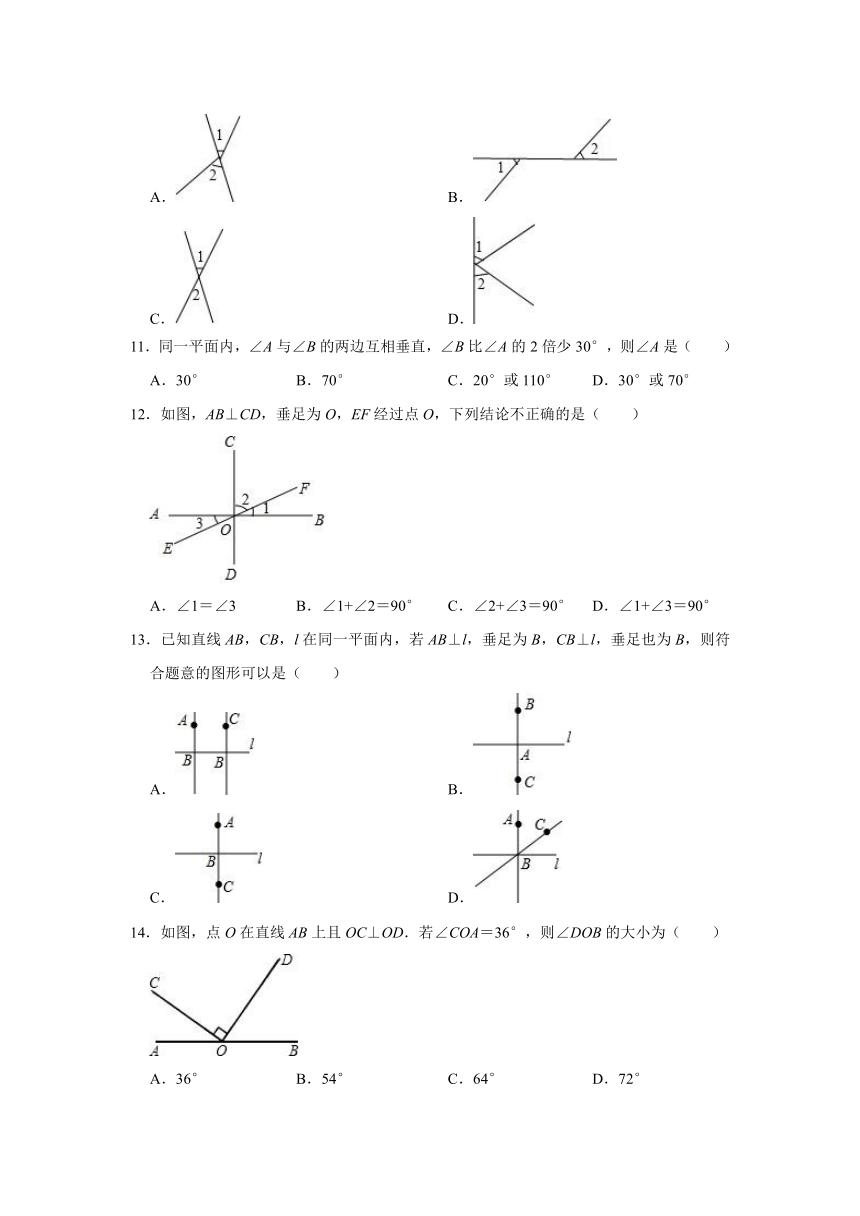
11.同一平面内,∠A与∠B的两边互相垂直,∠B比∠A的2倍少30°,则∠A是( )
A.30° B.70° C.20°或110° D.30°或70°
12.如图,AB⊥CD,垂足为O,EF经过点O,下列结论不正确的是( )
A.∠1=∠3 B.∠1+∠2=90° C.∠2+∠3=90° D.∠1+∠3=90°
13.已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
A. B.
C. D.
14.如图,点O在直线AB上且OC⊥OD.若∠COA=36°,则∠DOB的大小为( )
A.36° B.54° C.64° D.72°
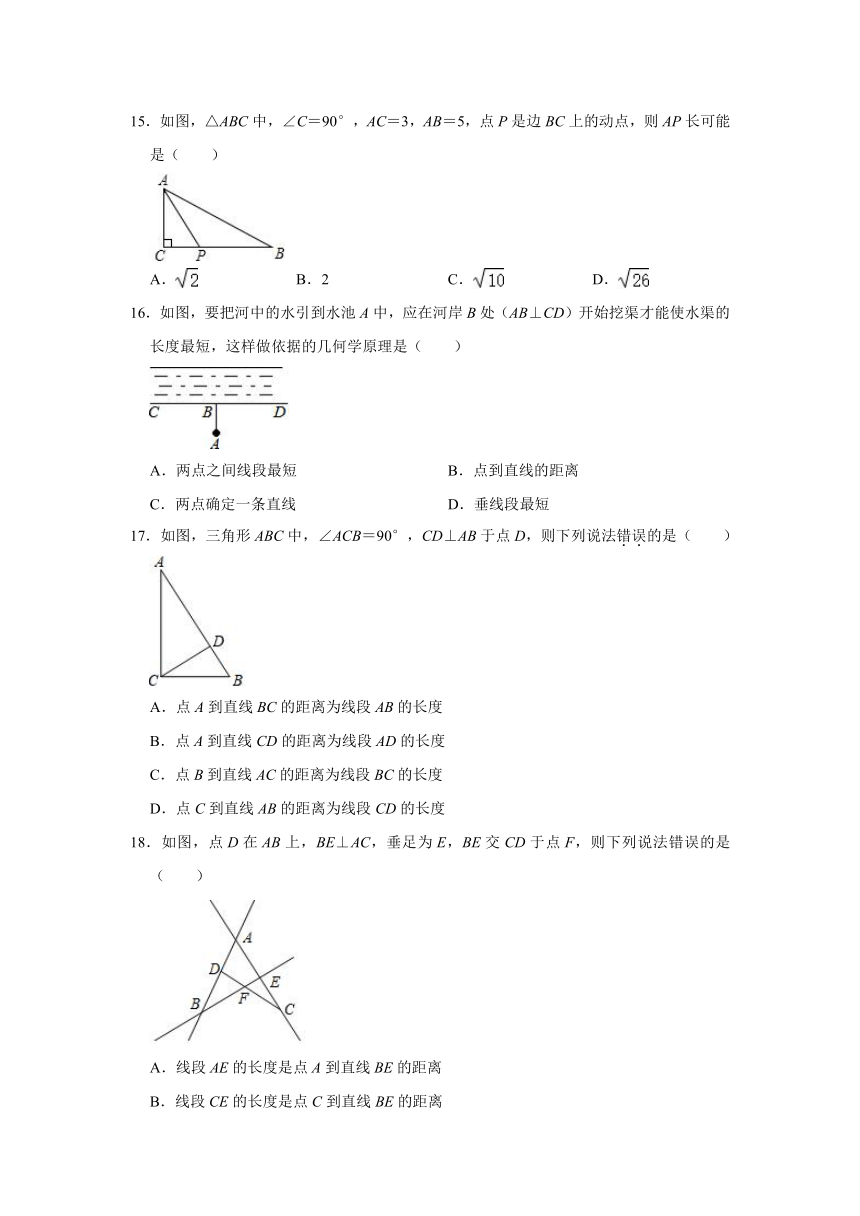
15.如图,△ABC中,∠C=90°,AC=3,AB=5,点P是边BC上的动点,则AP长可能是( )
A. B.2 C. D.
16.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
A.两点之间线段最短 B.点到直线的距离
C.两点确定一条直线 D.垂线段最短
17.如图,三角形ABC中,∠ACB=90°,CD⊥AB于点D,则下列说法错误的是( )
A.点A到直线BC的距离为线段AB的长度
B.点A到直线CD的距离为线段AD的长度
C.点B到直线AC的距离为线段BC的长度
D.点C到直线AB的距离为线段CD的长度
18.如图,点D在AB上,BE⊥AC,垂足为E,BE交CD于点F,则下列说法错误的是( )
A.线段AE的长度是点A到直线BE的距离
B.线段CE的长度是点C到直线BE的距离
C.线段FE的长度是点F到直线AC的距离
D.线段FD的长度是点F到直线AB的距离
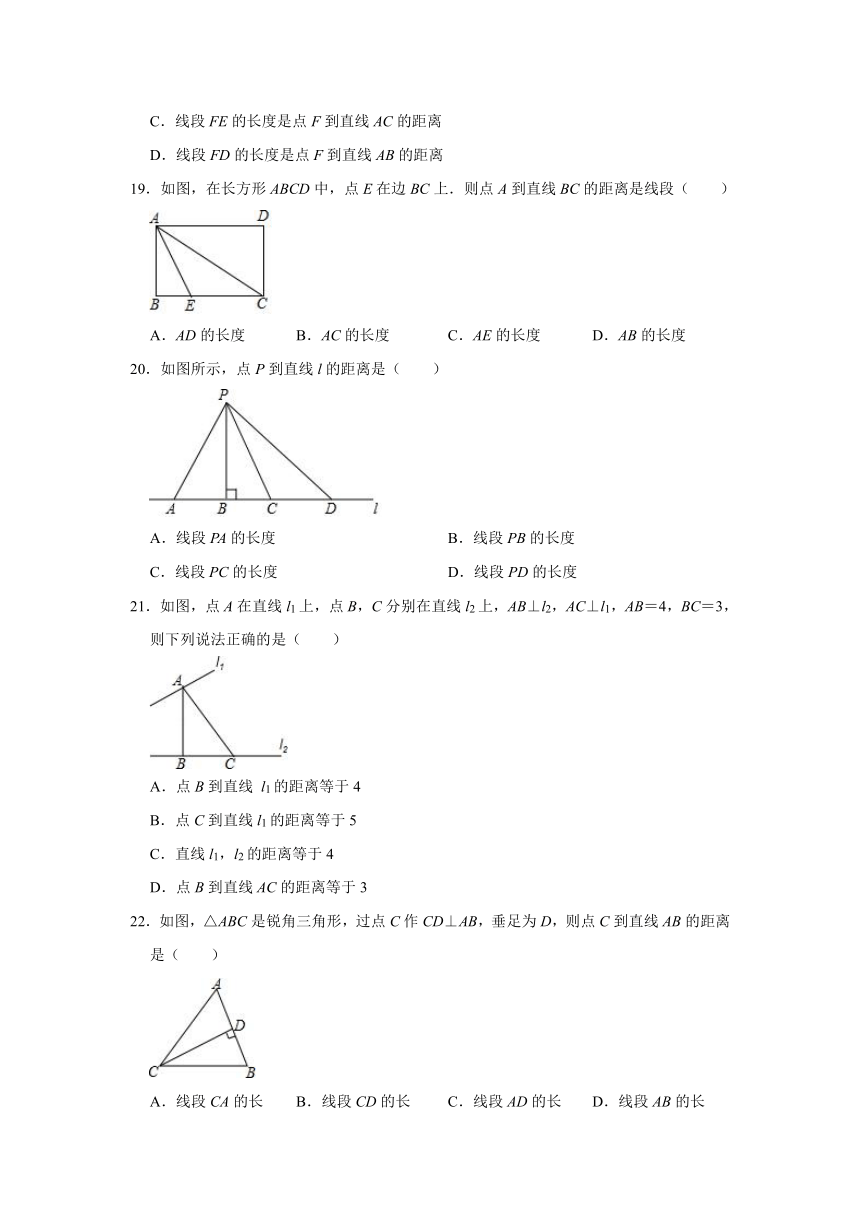
19.如图,在长方形ABCD中,点E在边BC上.则点A到直线BC的距离是线段( )
A.AD的长度 B.AC的长度 C.AE的长度 D.AB的长度
20.如图所示,点P到直线l的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段PD的长度
21.如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
A.点B到直线 l1的距离等于4
B.点C到直线l1的距离等于5
C.直线l1,l2的距离等于4
D.点B到直线AC的距离等于3
22.如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
A.线段CA的长 B.线段CD的长 C.线段AD的长 D.线段AB的长
23.点P为直线l外一点,点A、B、C为直线上三点,PA=3cm,PB=4cm,PC=5cm,则点P到直线l的距离为( )
A.2cm B.3cm C.小于3cm D.不大于3cm
24.如图,PO⊥OR,OQ⊥PR,则点O到PR所在的直线的距离是线段( )的长度.
A.PO B.RO C.OQ D.PQ
25.下列图形中,线段PQ的长表示点P到直线MN的距离是( )
A. B.
C. D.
26.点到直线的距离是( )
A.点到直线上一点的连线
B.点到直线的垂线
C.点到直线的垂线段
D.点到直线的垂线段的长度
27.如图,直线a,b被直线c所截,则∠4的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠5
28.如图,直线a、b被直线c所截,则与∠1是同位角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
29.如图,直线a,b被直线c所截,则∠2的内错角是( )
A.∠1 B.∠3 C.∠4 D.∠5
30.如图,四边形ABCD的对角线AC,BD交于点O,则∠DAC的内错角是( )
A.∠ABD B.∠BDC C.∠ACB D.∠DOC
31.如图,点E在BC的延长线上,则下列两个角是同位角的是( )
A.∠BAC和∠ACD B.∠D和∠BAD C.∠ACB和∠ACD D.∠B和∠DCE
32.如图,已知四边形ABCD,延长BC到点E,则∠DCE的同位角是( )
A.∠A B.∠B C.∠DCB D.∠D
33.如图,∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
34.两条直线被第三条直线所截,则( )
A.同位角不一定相等 B.内错角必相等
C.同旁内角必互补 D.同位角定相等
35.如图所示,图中∠1与∠2是同位角的是( )
A.1个 B.2个 C.3个 D.4个
36.如图,点E在四边形ABCD的边BC的延长线上,则下列两个角是同位角的是( )
A.∠BAC和∠ACB B.∠B和∠DCE C.∠B和∠BAD D.∠B和∠ACD
37.如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
38.如图,下列各语句中,错误的语句是( )
A.∠ADE与∠B是同位角 B.∠BDE与∠C是同旁内角
C.∠BDE与∠AED是内错角 D.∠BDE与∠DEC是同旁内角
二.填空题(共14小题)
39.如图,2条直线两两相交最多能有1个交点,3条直线两两相交最多能有3个交点,4条直线两两相交最多能有6个交点,5条直线两两相交最多能有 个交点,…,n条直线两两相交最多能有 个交点(用含有n的代数式表示)
40.如图,如果∠3=2∠1,则∠2= ,∠3= ,∠4= .
41.如图,直线a、b相交于点O,若∠1=50°,则∠2= °.
42.如图,直线AB,CD相交于点O,∠AOC=54°,∠1比∠2大10°,则∠1= 度;∠2= 度.
43.如图,直线AB与直线CD相交于点E,若∠BED=25°,则∠CEA= 度.
44.如图,直线AD、BC交于O点,∠AOB+∠COD=110°,则∠COD的度数为 °.
45.已知:如图直线AB与CD相交于点O,OE⊥AB,∠COE=60°,则∠BOD等于 度.
46.如图,AB⊥CD于点O,EF经过点O,∠1=27°,则∠AOE= ,∠COF= ,∠BOE= .
47.如图,要把池中的水引到D处,可过D点引DC⊥AB于C,然后沿DC开渠,可使所开渠道最短,试说明设计的依据: .
48.如图,点A,B,C,D,E在直线l上,点P在直线l外,PC⊥l于点C,在线段PA,PB,PC,PD,PE中,最短的一条线段是 ,理由是
49.如图,计划把水从河中引到水池A中,先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是 .
50.如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段 的长度,这样测量的依据是 .
51.如图,直线外一点P到直线m上的三点A、B、C的距离分别是PA=4,PB=6,PC=3,则点P到直线m的距离是 .
52.如图,∠DAB和∠B是直线DE和BC被直线 所截而形成的角,称它们为 角.
三.解答题(共8小题)
53.两条直线a、b相交,其中2∠3=3∠1,求∠2的度数.
54.如图,三条直线AB,CD,EF交于一点,若∠1=30°,∠2=70°,求∠3的度数.
55.如图所示,直线AB、CD相交于O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.
56.如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,AB⊥EF,求∠DOF和∠FOC的度数.
57.如图,已知OA⊥OB,∠AOC=∠BOD,试说明CO⊥DO.
58.如图,直线AB和CD相交于O点,OE⊥CD,∠EOF=122°,OD平分∠BOF,求∠AOF的度数.
59.如图,过点A作BC的垂线,并指出那条线的长度是表示点A到BC的距离?
60.已知点C在直线a外,点A在直线a上,且AC=2厘米.
(1)设d是点C到直线a的距离,求d的取值范围;
(2)若直线BD垂直于直线a,垂足为B.则直线BD与直线AC有怎样的位置关系,请画示意图表示(每种位置关系画一个示意图).
参考答案与试题解析
一.选择题(共38小题)
1.两条直线相交所成的四个角中,下列说法正确的是( )
A.一定有一个锐角 B.一定有一个钝角
C.一定有一个直角 D.一定有一个不是钝角
【分析】根据两条直线相交有垂直相交和斜交两种情况,所以A、B、C均考虑不全面,故选D.
【解答】解:因为两条直线相交,分为垂直相交和斜交,故分两种情况讨论:
①当两直线垂直相交时,四个角都是直角,故A、B错误;
②当两直线斜交时,有两个角是锐角,两个角是钝角,所以C错误;
综上所述,D正确.
故选:D.
2.下面四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
【分析】根据对顶角的定义,可得答案.
【解答】解:由对顶角的定义,得C是对顶角,
故选:C.
3.下面四个图形中,∠1与∠2是邻补角的是( )
A. B.
C. D.
【分析】根据邻补角的定义,相邻且互补的两个角互为邻补角进行判断.
【解答】解:A、B选项,∠1与∠2没有公共顶点且不相邻,不是邻补角;
C选项∠1与∠2不互补,不是邻补角;
D选项互补且相邻,是邻补角.
故选:D.
4.如图,已知点A,B,N在一条直线上,点F,B,M在一条直线上,点E,F在线段AD上,若∠MBN﹣∠X=∠ABE,则∠X=( )
A.∠EBF B.∠ABE C.∠ABF D.∠EBC
【分析】依据对顶角相等,可得∠MBN=∠ABF=∠ABE+∠EBF,再根据∠MBN﹣∠X=∠ABE,即可得到∠X=∠EBF.
【解答】解:∵点A,B,N在一条直线上,点F,B,M在一条直线上,
∴∠MBN=∠ABF=∠ABE+∠EBF,
又∵∠MBN﹣∠X=∠ABE,
∴∠X=∠EBF,
故选:A.
5.下列各组角中,∠1与∠2是对顶角的为( )
A. B.
C. D.
【分析】根据对顶角的定义即可判定.
【解答】解:(A)∠1与∠2没有公共顶点,故A错误;
(C)与(D)∠1与∠2的两边不是互为反向延长线,故C、D错误;
故选:B.
6.下面四个图形中∠1与∠2是对顶角的是( )
A. B.
C. D.
【分析】根据对顶角的定义作出判断即可.
【解答】解:根据对顶角的定义可知:只有C图中的是对顶角,其它都不是.
故选:C.
7.下列图形中∠1与∠2互为对顶角的是( )
A. B.
C. D.
【分析】根据对顶角的定义进行判断.
【解答】解:A、B、D中∠1与∠2不是对顶角,C中∠1与∠2互为对顶角.
故选:C.
8.下列图形中表示∠1与∠2是对顶角的是( )
A. B.
C. D.
【分析】两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角,由此可得出正确答案.
【解答】解:根据对顶角的定义可得B、C、D都不是对顶角,只有A选项符合对顶角的定义.
故选:A.
9.下列图形中,∠1、∠2是对顶角的是( )
A. B.
C. D.
【分析】根据对顶角的特征,有公共顶点,且两边互为反向延长线,对各选项分析判断后利用排除法求解.
【解答】解:A、∠1、∠2没有公共顶点,不是对顶角,故本选项错误;
B、∠1、∠2两边不互为反向延长线,不是对顶角,故本选项错误;
C、∠1、∠2两边不互为反向延长线,不是对顶角,故本选项错误;
D、∠1、∠2有公共顶点,两边互为反向延长线,是对顶角,故本选项正确.
故选:D.
10.如图,∠1与∠2是对顶角的是( )
A. B.
C. D.
【分析】根据对顶角的定义进行判断:两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做对顶角,依次判定即可得出答案.
【解答】解:A、∠1与∠2有一条边在同一条直线上,另一条边不在同一条直线上,不是对顶角,故A选项错误;
B、∠1与∠2没有公共顶点,不是对顶角,故B选项错误;
C、∠1与∠2的两边互为反向延长线,是对顶角,故C选项正确;
D、∠1与∠2有一条边在同一条直线上,另一条边不在同一条直线上,不是对顶角,故D选项错误.
故选:C.
11.同一平面内,∠A与∠B的两边互相垂直,∠B比∠A的2倍少30°,则∠A是( )
A.30° B.70° C.20°或110° D.30°或70°
【分析】因为两个角的两边分别垂直,则这两个角相等或互补,又因∠B比∠A的2倍少30°,所以它们互补,可设∠A是x度,利用方程即可解决问题.
【解答】解:设∠A是x度,根据题意,得
①两个角相等时,如图1:
∠B=∠A=x°,
x=2x﹣30
解得,x=30,
故∠A=30°,
②两个角互补时,如图2:
x+2x﹣30=180,
所以x=70,
故∠A=70°.
故选:D.
12.如图,AB⊥CD,垂足为O,EF经过点O,下列结论不正确的是( )
A.∠1=∠3 B.∠1+∠2=90° C.∠2+∠3=90° D.∠1+∠3=90°
【分析】根据垂直定义可得∠COB=90°,根据对顶角相等可得∠1=∠3,再利用余角性质可得答案.
【解答】解:A、∠1=∠3正确,故此选项不合题意;
B、∵AB⊥CD,
∴∠1+∠2=90°,故此选项不合题意;
C、∵∠1+∠2=90°,∠1=∠3,
∴∠2+∠3=90°,故此选项不合题意;
D、∠1+∠3=90°,错误,故此选项符合题意;
故选:D.
13.已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
A. B.
C. D.
【分析】根据题意画出图形即可.
【解答】解:根据题意可得图形,
故选:C.
14.如图,点O在直线AB上且OC⊥OD.若∠COA=36°,则∠DOB的大小为( )
A.36° B.54° C.64° D.72°
【分析】首先由OC⊥OD,根据垂直的定义,得出∠COD=90°,然后由平角的定义,知∠AOC+∠COD+∠DOB=180°,从而得出∠DOB的度数.
【解答】解:∵OC⊥OD,
∴∠COD=90°,
∵∠AOC+∠COD+∠DOB=180°,
∴∠DOB=180°﹣36°﹣90°=54°.
故选:B.
15.如图,△ABC中,∠C=90°,AC=3,AB=5,点P是边BC上的动点,则AP长可能是( )
A. B.2 C. D.
【分析】从直线外一点到这条直线所作的垂线段最短,根据垂线段最短,可得答案.
【解答】解:∵∠C=90°,点P在边BC上运动,
∴AB≥AP≥AC,
又∵AC=3,AB=5,
∴AP的长可能是,
故选:C.
16.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
A.两点之间线段最短 B.点到直线的距离
C.两点确定一条直线 D.垂线段最短
【分析】根据垂线段的性质:垂线段最短进行解答.
【解答】解:要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是:垂线段最短,
故选:D.
17.如图,三角形ABC中,∠ACB=90°,CD⊥AB于点D,则下列说法错误的是( )
A.点A到直线BC的距离为线段AB的长度
B.点A到直线CD的距离为线段AD的长度
C.点B到直线AC的距离为线段BC的长度
D.点C到直线AB的距离为线段CD的长度
【分析】根据点到直线的距离为点到直线的垂线段的长度来分析即可.
【解答】解:∵∠ACB=90°,
∴AC⊥BC
根据点到直线的距离为点到直线的垂线段的长度来分析:
A:点A到直线BC的距离为线段AC的长度,而不是线段AB的长度,故A错误.
故选:A.
18.如图,点D在AB上,BE⊥AC,垂足为E,BE交CD于点F,则下列说法错误的是( )
A.线段AE的长度是点A到直线BE的距离
B.线段CE的长度是点C到直线BE的距离
C.线段FE的长度是点F到直线AC的距离
D.线段FD的长度是点F到直线AB的距离
【分析】根据点到直线的距离定义作出正确的选择.
【解答】解:A、因为BE⊥AC,所以线段AE的长度是点A到直线BE的距离,说法正确,故本选项错误;
B、因为BE⊥AC,所以线段CE的长度是点C到直线BE的距离,说法正确,故本选项错误;
C、因为BE⊥AC,所以线段FE的长度是点F到直线AC的距离,说法正确,故本选项错误;
D、当CD⊥AB时,线段FD的长度是点F到直线AB的距离,说法错误,故本选项正确.
故选:D.
19.如图,在长方形ABCD中,点E在边BC上.则点A到直线BC的距离是线段( )
A.AD的长度 B.AC的长度 C.AE的长度 D.AB的长度
【分析】直线外一点到直线的垂线段的长度,叫做点到直线的距离.
【解答】解:∵AB⊥BC于B,
∴点A到直线BC的距离是线段AB的长度,
故选:D.
20.如图所示,点P到直线l的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段PD的长度
【分析】根据点到直线的距离是垂线段的长度,可得答案.
【解答】解:由题意,得
点P到直线l的距离是线段PB的长度,
故选:B.
21.如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
A.点B到直线 l1的距离等于4
B.点C到直线l1的距离等于5
C.直线l1,l2的距离等于4
D.点B到直线AC的距离等于3
【分析】根据点到直线的距离,即可解答.
【解答】解:∵AB⊥l2,AB=4,BC=3,
∴AC==5.
A、∵AB不垂直与l1,∴点B到直线 l1的距离不等于4,故本选项错误;
B、∵AC⊥l1,∴点C到直线l1的距离等于5,正确;
C、直线l1,l2的距离不等于4,故本选项错误;
D、点B到直线AC的距离等于,故本选项错误;
故选:B.
22.如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
A.线段CA的长 B.线段CD的长 C.线段AD的长 D.线段AB的长
【分析】根据点到直线的距离:直线外一点到直线的垂线段的长度,叫做点到直线的距离,可得点C到直线AB的距离是线段CD的长,据此解答即可.
【解答】解:如图,,
根据点到直线的距离的含义,可得
点C到直线AB的距离是线段CD的长.
故选:B.
23.点P为直线l外一点,点A、B、C为直线上三点,PA=3cm,PB=4cm,PC=5cm,则点P到直线l的距离为( )
A.2cm B.3cm C.小于3cm D.不大于3cm
【分析】根据直线外一点到直线的垂线段的长度,叫做点到直线的距离,可得连接直线外一点P与直线上任意点,所得线段中垂线段最短;然后根据PA=3cm,PB=4cm,PC=5cm,可得三条线段的最短的是3cm,所以点P到直线l的距离不大于3cm,据此判断即可.
【解答】解:连接直线外一点P与直线上任意点,所得线段中垂线段最短;
因为PA=3cm,PB=4cm,PC=5cm,
所以三条线段的最短的是3cm,
所以点P到直线l的距离不大于3cm.
故选:D.
24.如图,PO⊥OR,OQ⊥PR,则点O到PR所在的直线的距离是线段( )的长度.
A.PO B.RO C.OQ D.PQ
【分析】根据点到直线的距离的定义,从直线外一点到这条直线的垂线段长度,叫点到直线的距离解答.
【解答】解:根据点到直线的距离的定义,点O到PR所在的直线的距离是线段OQ的长度.
故选:C.
25.下列图形中,线段PQ的长表示点P到直线MN的距离是( )
A. B.
C. D.
【分析】利用点到直线的距离的定义分析可知.
【解答】解:利用点到直线的距离的定义可知:线段PQ的长表示点P到直线MN的距离的是A图.
故选:A.
26.点到直线的距离是( )
A.点到直线上一点的连线
B.点到直线的垂线
C.点到直线的垂线段
D.点到直线的垂线段的长度
【分析】根据从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,直接判断.
【解答】解:点到直线的距离是指点到直线的垂线段的长度,故选D.
27.如图,直线a,b被直线c所截,则∠4的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠5
【分析】根据内错角定义判断即可.
【解答】解:∠4的内错角是∠2,
故选:B.
28.如图,直线a、b被直线c所截,则与∠1是同位角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
【分析】直接利用同位角的定义分析得出答案.
【解答】解:直线a、b被直线c所截,则与∠1是同位角的是∠2.
故选:A.
29.如图,直线a,b被直线c所截,则∠2的内错角是( )
A.∠1 B.∠3 C.∠4 D.∠5
【分析】根据内错角的定义判断即可.
【解答】解:∠2的内错角是∠4,
故选:C.
30.如图,四边形ABCD的对角线AC,BD交于点O,则∠DAC的内错角是( )
A.∠ABD B.∠BDC C.∠ACB D.∠DOC
【分析】内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
【解答】解:∠DAC的内错角是∠ACB.
故选:C.
31.如图,点E在BC的延长线上,则下列两个角是同位角的是( )
A.∠BAC和∠ACD B.∠D和∠BAD C.∠ACB和∠ACD D.∠B和∠DCE
【分析】直接利用内错角、同旁内角、同位角的定义分别分析得出答案.
【解答】解:A、∠BAC和∠ACD,是内错角,故此选项错误;
B、∠D和∠BAD,是同旁内角,故此选项错误;
C、∠ACB和∠ACD,是相邻的角,故此选项错误;
D、∠B和∠DCE是同位角,故此选项正确.
故选:D.
32.如图,已知四边形ABCD,延长BC到点E,则∠DCE的同位角是( )
A.∠A B.∠B C.∠DCB D.∠D
【分析】同位角就是:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角.
【解答】解:∠DCE的同位角是∠B.
故选:B.
33.如图,∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
【分析】根据同位角的定义即可求出答案.
【解答】解:两条直线a,b被第三条直线c所截(或说a,b相交c),在截线c的同旁,被截两直线a,b的同一侧的角,我们把这样的两个角称为同位角.
故选:A.
34.两条直线被第三条直线所截,则( )
A.同位角不一定相等 B.内错角必相等
C.同旁内角必互补 D.同位角定相等
【分析】当两条互相平行的直线被第三条直线所截,截得的同位角相等,内错角相等,同旁内角互补,根据题意,两直线不平行,所B、C、D三项均不正确.
【解答】解:∵两条被截的直线不平行,
∴截得的同位角不一定相等,内错角不一定相等,同旁内角不一定互补,
故选:A.
35.如图所示,图中∠1与∠2是同位角的是( )
A.1个 B.2个 C.3个 D.4个
【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
【解答】解:根据同位角的定义,可得图(1)(2)(4)中,∠1与∠2在两直线的同侧,并且在第三条直线(截线)的同旁,故是同位角,
而图(3)中,∠1与∠2不是两条直线被第三条直线所截形成的同位角.
故选:C.
36.如图,点E在四边形ABCD的边BC的延长线上,则下列两个角是同位角的是( )
A.∠BAC和∠ACB B.∠B和∠DCE C.∠B和∠BAD D.∠B和∠ACD
【分析】利用同位角、内错角及同旁内角的定义分别判断后即可确定正确的选项.
【解答】解:A、∠BAC和∠ACB是同旁内角,不符合题意;
B、∠B和∠DCE是同位角,符合题意;
C、∠B和∠BAD是同旁内角,不符合题意;
D、∠B和∠ACD不属于同位角、内错角及同旁内角的任何一种,不符合题意,
故选:B.
37.如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
【分析】根据内错角的定义找出即可.
【解答】解:根据内错角的定义,∠1的内错角是∠5.
故选:D.
38.如图,下列各语句中,错误的语句是( )
A.∠ADE与∠B是同位角 B.∠BDE与∠C是同旁内角
C.∠BDE与∠AED是内错角 D.∠BDE与∠DEC是同旁内角
【分析】根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角作答.
【解答】解:A、由同位角的概念可知,∠ADE与∠B是同位角,不符合题意;
B、由同位角同旁内角的概念可知,∠BDE与∠C不是同旁内角,符合题意;
C、由内错角的概念可知,∠BDE与∠AED是内错角,不符合题意;
D、由同旁内角的概念可知,∠BDE与∠DEC是同旁内角,不符合题意.
故选:B.
二.填空题(共14小题)
39.如图,2条直线两两相交最多能有1个交点,3条直线两两相交最多能有3个交点,4条直线两两相交最多能有6个交点,5条直线两两相交最多能有 10 个交点,…,n条直线两两相交最多能有 个交点(用含有n的代数式表示)
【分析】根据题目中的交点个数,找出n条直线相交最多有的交点个数公式:.
【解答】解:2条直线相交有1个交点;
3条直线相交有1+2=3个交点;
4条直线相交有1+2+3=6个交点;
5条直线相交有1+2+3+4=10个交点;
6条直线相交有1+2+3+4+5=15个交点;
…
n条直线相交有1+2+3+5+…+(n﹣1)=个交点.
故答案为:10;.
40.如图,如果∠3=2∠1,则∠2= 2∠1 ,∠3= ∠2 ,∠4= ∠1 .
【分析】根据对顶角的定义进而将已知代入求出即可.
【解答】解:如果∠3=2∠1,则∠2=2∠1,∠3=∠2,∠4=∠1.
故答案为:2∠1,∠2,∠1.
41.如图,直线a、b相交于点O,若∠1=50°,则∠2= 130 °.
【分析】由直线a、b相交于点O,可知∠1、∠2是邻补角,所以,∠1+∠2=180°,代入∠1=50°,可求出∠2的度数;
【解答】解:∵直线a、b相交于点O,
∴∠1+∠2=180°,
∵∠1=50°,
∴∠2=180°﹣50°=130°,
故答案为130°.
42.如图,直线AB,CD相交于点O,∠AOC=54°,∠1比∠2大10°,则∠1= 32 度;∠2= 22 度.
【分析】由两直线相交,对顶角相等,可得∠AOC=∠BOD=54°,即∠1+∠2=54°,结合已知∠1比∠2大10°,解方程组即可.
【解答】解:∵∠AOC与∠BOD是对顶角,
∴∠1+∠2=∠AOC=54°,
∵∠1﹣∠2=10°,
∴∠1=32°,∠2=22°.
43.如图,直线AB与直线CD相交于点E,若∠BED=25°,则∠CEA= 25 度.
【分析】结合图形,根据对顶角相等直接求∠CEA的度数即可.
【解答】解:由图可知,∠BED和∠CEA是对顶角,
∴∠CEA=∠BED=25°.
44.如图,直线AD、BC交于O点,∠AOB+∠COD=110°,则∠COD的度数为 55 °.
【分析】结合图形可知,∠AOB与∠COD是对顶角,且对顶角相等,代入∠AOB+∠COD=110°,即可得∠COD的度数.
【解答】解:∵∠AOB=∠COD,
又∵∠AOB+∠COD=110°,
∴2∠COD=110°,即∠COD=55°.
45.已知:如图直线AB与CD相交于点O,OE⊥AB,∠COE=60°,则∠BOD等于 30 度.
【分析】根据垂线的定义,可得∠AOE的度数,根据余角的性质,可得∠AOC的度数,根据对顶角相等,可得答案.
【解答】解:由垂线的定义,得
∠AOE=90°,
由余角的性质,得
∠AOC=∠AOE﹣∠COE=30°,
由对顶角相等,得
∠BOD=∠AOC=30°,
故答案为:30.
46.如图,AB⊥CD于点O,EF经过点O,∠1=27°,则∠AOE= 27° ,∠COF= 63° ,∠BOE= 153° .
【分析】首先利用对顶角定义得出∠AOE的度数,进而利用互余关系求出各角的度数即可.
【解答】解:∵AB⊥CD于点O,EF经过点O,∠1=27°,
∴∠AOE=27°,
∴∠COF=90°﹣∠1=63°,
∵∠COF=∠DOE=63°,
∴∠BOE=90°+63°=153°.
故答案为:27°,63°,153°.
47.如图,要把池中的水引到D处,可过D点引DC⊥AB于C,然后沿DC开渠,可使所开渠道最短,试说明设计的依据: 垂线段最短 .
【分析】根据垂线段的性质,可得答案.
【解答】解:要把池中的水引到D处,可过D点引DC⊥AB于C,然后沿DC开渠,可使所开渠道最短,试说明设计的依据:垂线段最短.
故答案为:垂线段最短.
48.如图,点A,B,C,D,E在直线l上,点P在直线l外,PC⊥l于点C,在线段PA,PB,PC,PD,PE中,最短的一条线段是 PC ,理由是 垂线段最短
【分析】点到直线的距离是指该点到直线的垂线段的长,根据定义即可选出答案.
【解答】解:根据点到直线的距离的定义得出线段PC的长是点P到直线l的距离,从直线外一点到这条直线所作的垂线段最短.
故答案是:PC;垂线段最短.
49.如图,计划把水从河中引到水池A中,先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是 垂线段最短 .
【分析】根据垂线段的性质,可得答案.
【解答】解:先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是垂线段最短;
故答案为:垂线段最短.
50.如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段 BN 的长度,这样测量的依据是 垂线段最短 .
【分析】由点到直线的距离的定义及跳远比赛的规则作出分析和判断.
【解答】解:他的跳远成绩是线段BN的长度.
故答案为:BN,垂线段最短.
51.如图,直线外一点P到直线m上的三点A、B、C的距离分别是PA=4,PB=6,PC=3,则点P到直线m的距离是 不大于3 .
【分析】根据“直线外一点到直线上各点的所有线中,垂线段最短”进行解答.
【解答】解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,
∴点P到直线m的距离≤PC,
即点P到直线m的距离不大于3.
故答案为:不大于3
52.如图,∠DAB和∠B是直线DE和BC被直线 AB 所截而形成的角,称它们为 内错 角.
【分析】内错角,“内”指在被截两条直线之间;“错”即交错,在第三条直线的两侧.(一个角在第三条直线左侧,另一角在第三条直线右侧).
【解答】解:∠DAB和∠B是直线DE和BC被直线AB所截而形成的角,称它们为内错角.
三.解答题(共8小题)
53.两条直线a、b相交,其中2∠3=3∠1,求∠2的度数.
【分析】根据邻补角的性质,可得∠1的度数,根据对顶角的性质,可得答案.
【解答】解;∵2∠3=3∠1,∠3=∠1,
∠1与∠3是邻补角,
∴∠1+∠3=180°,
∠1=72°,
由邻补角的性质得∠2=180°﹣∠1=108°.
54.如图,三条直线AB,CD,EF交于一点,若∠1=30°,∠2=70°,求∠3的度数.
【分析】根据对顶角相等可得∠4=∠2,然后利用平角的定义列式计算即可得解.
【解答】解:如图,∵∠4=∠2=70°(对顶角相等),
∴∠3=180°﹣∠1﹣∠4=180°﹣30°﹣70°=80°.
55.如图所示,直线AB、CD相交于O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.
【分析】由已知∠FOC=90°,∠1=40°结合平角的定义,可得∠3的度数,又因为∠3与∠AOD互为邻补角,可求出∠AOD的度数,又由OE平分∠AOD可求出∠2.
【解答】解:∵∠FOC=90°,∠1=40°,AB为直线,
∴∠3+∠FOC+∠1=180°,
∴∠3=180°﹣90°﹣40°=50°.
∠3与∠AOD互补,
∴∠AOD=180°﹣∠3=130°,
∵OE平分∠AOD,
∴∠2=∠AOD=65°.
56.如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,AB⊥EF,求∠DOF和∠FOC的度数.
【分析】(1)根据邻补角的定义即可得到结论;
(2)根据对顶角的定义得到结论;
(3)由垂直的定义得到∠AOF=∠BOF=90°,根据角的和差即可得到结论.
【解答】解:(1)∠COE的邻补角为∠COF和∠EOD;
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF;
(3)∵AB⊥EF,
∴∠AOF=∠BOF=90°,
∴∠DOF=∠BOF﹣∠BOD=90°﹣60°=30°,
又∵∠AOC=∠BOD=60°,
∴∠FOC=∠AOF+∠AOC=90°+60°=150°.
57.如图,已知OA⊥OB,∠AOC=∠BOD,试说明CO⊥DO.
【分析】根据垂线的定义,可得∠AOB,根据等式的性质,可得∠COD,根据垂线的定义,可得答案.
【解答】证明:∵OA⊥OB,
∴∠AOB=90°.
∵∠AOC=∠BOD,
∴∠AOC﹣∠BOC=∠BOD﹣∠BOC,
即∠COD=∠AOB=90°,
∴CO⊥DO.
58.如图,直线AB和CD相交于O点,OE⊥CD,∠EOF=122°,OD平分∠BOF,求∠AOF的度数.
【分析】根据垂直,可得∠DOE的度数,根据角的和差,可得∠FOD的度数,根据角平分线,可得∠BOF的度数,根据∠BOF与∠AOF是邻补角,可得答案.
【解答】解:OE⊥CD,
∴∠EOD=90°,
∵∠EOF=122°,
∴∠DOF=122°﹣90°=32°.
∵OD平分∠BOF,
∴∠BOF=2∠DOF=64°,
∵∠AOF+∠BOF=180°,
∴∠AOF=180°﹣∠BOF=180°﹣64°=116°.
59.如图,过点A作BC的垂线,并指出那条线的长度是表示点A到BC的距离?
【分析】根据点到直线的距离的定义,过点A作BC的垂线,交CB的延长线于E,即可得到答案.
【解答】解:过点A作BC的垂线,交CB的延长线于E,
根据点到直线的距离的定义:从直线外一点到这条直线的垂线段长度,叫点到直线的距离.
可得AE的长度即为点A到BC的距离.
答:AE的长度即为点A到BC的距离.
60.已知点C在直线a外,点A在直线a上,且AC=2厘米.
(1)设d是点C到直线a的距离,求d的取值范围;
(2)若直线BD垂直于直线a,垂足为B.则直线BD与直线AC有怎样的位置关系,请画示意图表示(每种位置关系画一个示意图).
【分析】(1)由于点C在直线a外,所以AC和直线a有两种可能:①垂直相交,此时d=AC;②不垂直相交,此时d<AC.由此即可确定d的取值范围;
(2)如图,有四种位置关系:分别是重合、相交(两种)、平行.
【解答】(1)解:∵当AC⊥直线a时,A为垂足,此时d=AC=2厘米,
∴0<d≤2;
(2)解:如图所示:
,
标出AC与BD交于点E.
