北师大版九年级数学下册3.4圆周角和圆心角的关系第一课时 课件(25张ppt)
文档属性
| 名称 | 北师大版九年级数学下册3.4圆周角和圆心角的关系第一课时 课件(25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 355.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-19 08:36:44 | ||
图片预览





文档简介
(共25张PPT)
welcome
欢迎您!
3.4 圆周角和圆心角的关系
北师大版初中数学九年级下册第三章《圆》
第一课时 课件
一、教学目标及教学重难点:
1、教学目标:
知识目标:理解圆周角的概念,掌握圆周角和圆心角之间的关系,并会运用它进行有关的证明和运算.
能力目标:经历探索圆周角和圆心角关系的过程,培养学生观察、分析、猜想、归纳和逻辑推理的能力;通过渗透分类讨论、转化、归纳等数学思想方法,培养学生的探究意识和探索新知识的能力.
情感目标:在探索圆周角和圆心角关系的过程中,引导学生对图形的观察、发现,激发学生的好奇心和求知欲,并在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心.
2、教学重点:本着课程标准,在吃透教材基础上,我觉得本节课的教学的重点是理解圆周角的概念;掌握圆周角与圆心角之间的关系定理.
3、教学难点:圆周角和圆心角关系定理的证明.
二、学情分析:
学生已经了解圆中的基本概念,会判断圆心角,基本掌握圆心角的相关性质,熟练掌握了三角形外角和定理.初三学生已经具备一定的独立思考和探索能力,并能在探索过程中形成自己的观点,能在倾听别人意见的过程中逐渐完善自己的想法.因此,本节课设计了自学和探究活动,给学生提供自主探索与交流的空间,体现知识的形成过程.
三、教学过程:
巧设情境 激发兴趣
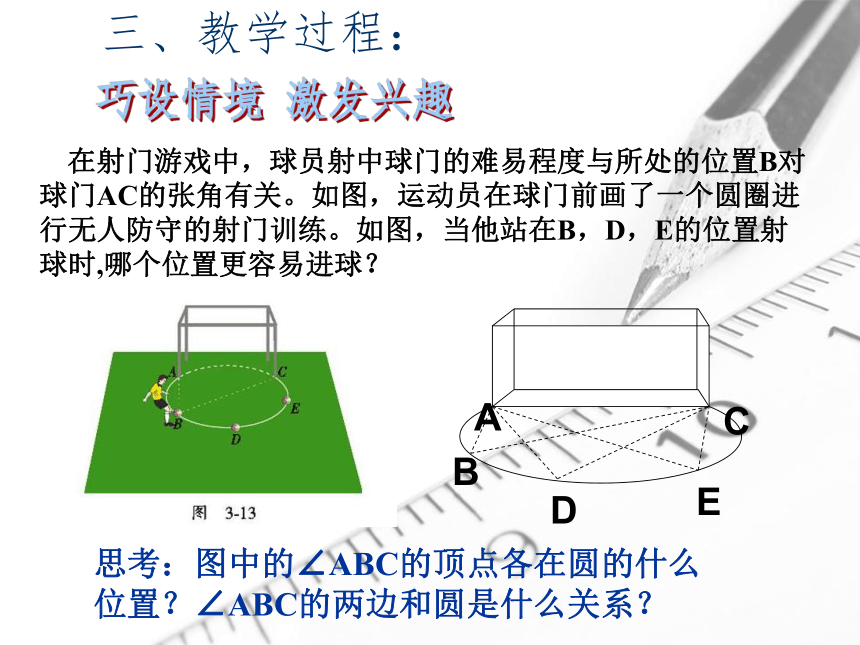
在射门游戏中,球员射中球门的难易程度与所处的位置B对球门AC的张角有关。如图,运动员在球门前画了一个圆圈进行无人防守的射门训练。如图,当他站在B,D,E的位置射球时,哪个位置更容易进球?
A
B
C
D
E
思考:图中的∠ABC的顶点各在圆的什么位置?∠ABC的两边和圆是什么关系?
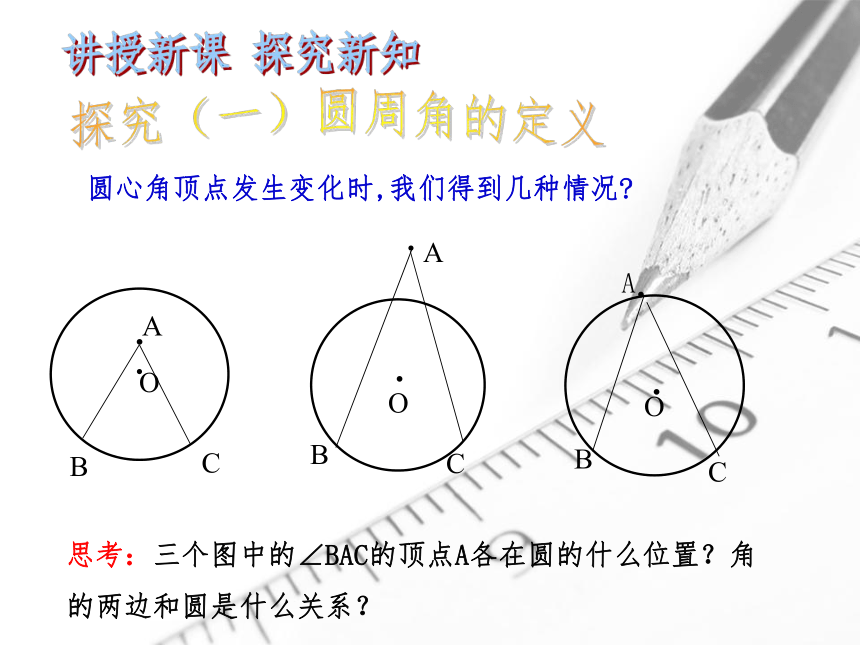
圆心角顶点发生变化时,我们得到几种情况?
A
.
O
B
C
.
思考:三个图中的∠BAC的顶点A各在圆的什么位置?角的两边和圆是什么关系?
.
.
A
O
B
C
A
.
O
B
C
.
讲授新课 探究新知
探究(一)圆周角的定义
B
A
C
A
B
C
D
E
●O
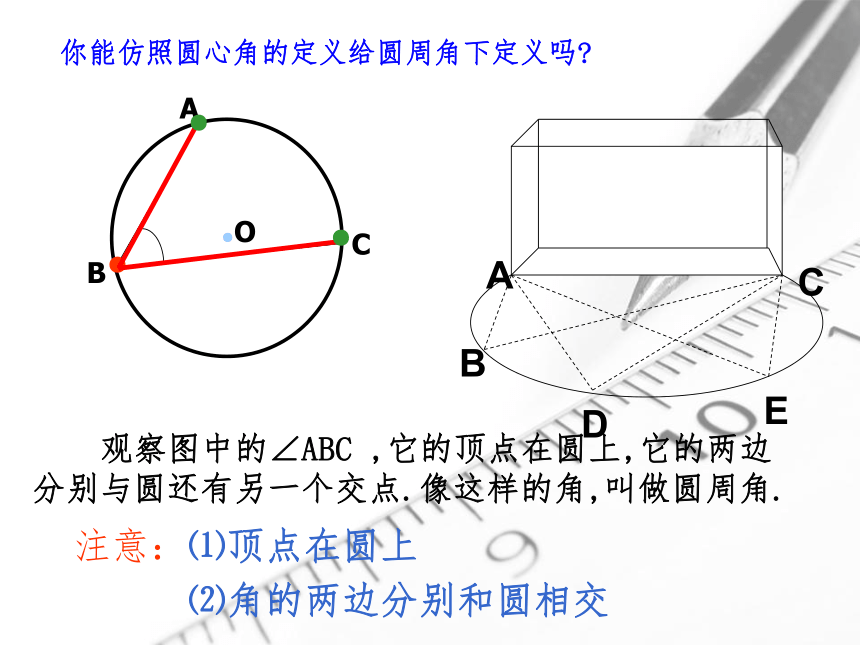
观察图中的∠ABC ,它的顶点在圆上,它的两边分别与圆还有另一个交点.像这样的角,叫做圆周角.
⑵角的两边分别和圆相交
●
注意:
⑴顶点在圆上
●
●
你能仿照圆心角的定义给圆周角下定义吗?
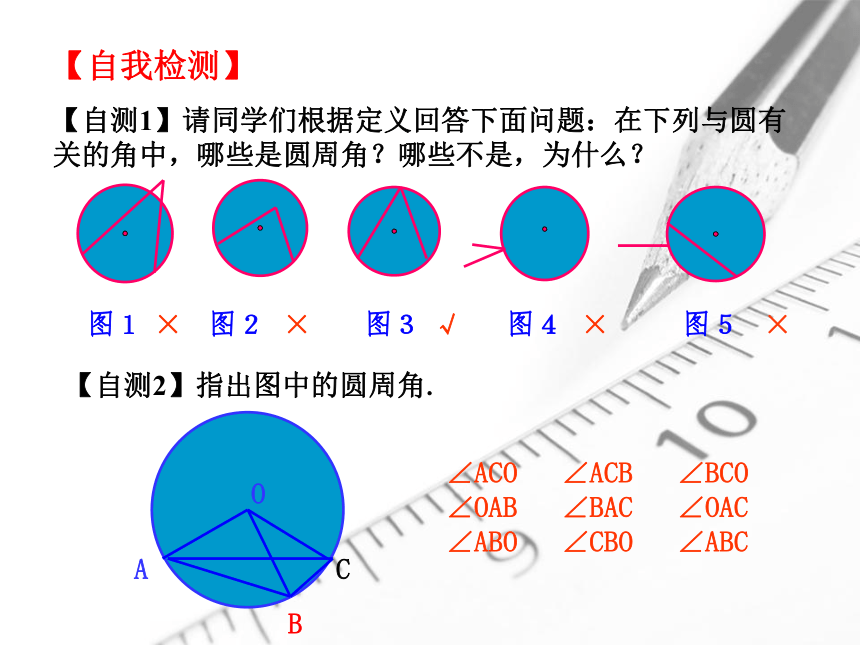
【自测1】请同学们根据定义回答下面问题:在下列与圆有关的角中,哪些是圆周角?哪些不是,为什么?
图1
图2
图3
图4
图5
【自测2】指出图中的圆周角.
A
O
B
C
∠ACO ∠ACB ∠BCO ∠OAB ∠BAC ∠OAC ∠ABO ∠CBO ∠ABC
×
×
√
×
×
【自我检测】
在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.
学科网
探究(二)圆周角和圆心角的关系
活动(一)
做一做
请同学们在圆上确定一条劣弧,画出它所对的圆心角与圆周角。
A
C
O
请你动手画出⊙0中弧AC所对的圆心角和圆周角,观察弧AC所对的圆周角有几个?它们的大小有什么关系?
如图,观察弧AC所对的圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?
说说你的想法,并与同伴交流.
提示:注意圆心与圆周角的位置关系.
A
B
C
●O
A
B
C
●O
●O
A
B
C
圆心在圆周角的一边上
圆心在圆周角的内部
圆心在圆周角的外部
改变圆心角∠AOC的度数,你得到的结论还成立吗?
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
●O
A
B
C
∴∠A=∠B.
∴∠AOC=2∠B.
即 ∠ABC = ∠AOC.
你能写出这个命题吗?
一条弧所对的圆周角等于它所对的圆心角的一半.
活动(二)
议一议
如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
老师提示:能否转化为1的情况?
过点B作直径BD.由1可得:
●O
∴ ∠ABC = ∠AOC.
你能写出这个命题吗?
A
B
C
D
∠ABD = ∠AOD,∠CBD = ∠COD,
一条弧所对的圆周角等于它所对的圆心角的一半.
如果圆心不在圆周角的一边上,结果会怎样?
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
老师提示:能否也转化为1的情况?
过点B作直径BD.由1可得:
●O
∴∠ABC = ∠AOC.
你能写出这个命题吗?
D
∠ABD = ∠AOD,∠CBD = ∠COD,
A
B
C
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即∠ABC= ∠AOC.
D
D
圆心在角的边
圆心在角
圆心在角
上
内
外
定理:
B
A
O
.
70°
x
【自测3】求圆中角x的度数
C
A
O
.
x
120°
A
O
.
120°
C
D
B
【自我检测】
【自测4】如图,已知圆心角∠AOB=100°,求圆周角∠ADB、∠ACB的度数?
【自我检测】
探究(三)圆周角和圆心角的关系
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成的圆周角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?
A
B
C
D
E
圆上一条弧所对的圆周角能做出几个?它们之间有什么关系?
结论:同弧或等弧所对的圆周角相等。
【自测5】试找出下图中所有相等的圆周角。
A
B
C
D
1
2
3
4
5
6
7
8
∠2=∠7
∠1=∠4
∠3=∠6
∠5=∠8
【自我检测】
例1.如图,OA,OB,OC都是⊙O的半径,∠AOB=2∠BOC.则∠ACB与∠BAC的大小有什么关系?为什么?
O
C
A
B
1
2
3
4
解: ∵∠1= ∠3
∠2= ∠4
∠3=2∠4
1
2
__
1
2
__
即∠ACB=2∠BAC
∴∠1=2∠2
答:∠ACB=2∠BAC.
自主学习 合作探究
活动(三)
堂堂测
思考:例2、圆中一条弦所对的圆周角有几个,它们都相等吗?
计算:(1)等于半径的弦对的圆周角 .
(2)半径为R的圆中,有一条弦分圆周成1:2两部分,则弦所对的圆周角的度数是__。
【延伸拓展】
达标检测 及时反馈
1、如图,△ABC内接于⊙O,∠BOC=130°,则∠A的度数为( ).
2、如图,△ABC内接于⊙O,∠ABC=45°,∠ACB=75°,则∠BOC的度数为( ).
3、一条弦分圆为1:4两部分,求这弦所对的圆周角的度数?
4、如图3,有一圆形展厅,在其圆形边缘上的点A处安装了一台监视器,它的监控角度是65°,为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器台.
5、如图5,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则 ∠DCF=__ .
图1
图2
6、拓展练习:
(1)如图,OA、OB、OC都是圆O的半径,
如果:∠AOB=2∠BOC.
求证:∠ACB=2∠BAC
(2)如果∠AOC=100°,则∠ABC=( ).
(3)如果点A、B、C在⊙O中,∠CAB=25°,∠ACB=30°,求弦AC所对圆周角的度数.
课堂小结 知识内化
1、什么是圆周角?它和圆心角有什么不同?
2、圆周角和圆心有几种位置关系?
3、圆周角和圆心角的关系定理是什么?它使用的前提条件是什么?
4、你是如何证明圆周角和圆心角之间的关系的?证明过程中用了哪些数学方法呢?
5、圆周角及圆周角定理的应用极其广泛,也是中考的一个重要考点,望同学们灵活运用.
布置作业 巩固提高
必做题:教材第80至81页第1、2题
选做题:探讨“在同圆或等圆中,相等的弦所对的圆周角的关系”。
welcome
欢迎您!
3.4 圆周角和圆心角的关系
北师大版初中数学九年级下册第三章《圆》
第一课时 课件
一、教学目标及教学重难点:
1、教学目标:
知识目标:理解圆周角的概念,掌握圆周角和圆心角之间的关系,并会运用它进行有关的证明和运算.
能力目标:经历探索圆周角和圆心角关系的过程,培养学生观察、分析、猜想、归纳和逻辑推理的能力;通过渗透分类讨论、转化、归纳等数学思想方法,培养学生的探究意识和探索新知识的能力.
情感目标:在探索圆周角和圆心角关系的过程中,引导学生对图形的观察、发现,激发学生的好奇心和求知欲,并在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心.
2、教学重点:本着课程标准,在吃透教材基础上,我觉得本节课的教学的重点是理解圆周角的概念;掌握圆周角与圆心角之间的关系定理.
3、教学难点:圆周角和圆心角关系定理的证明.
二、学情分析:
学生已经了解圆中的基本概念,会判断圆心角,基本掌握圆心角的相关性质,熟练掌握了三角形外角和定理.初三学生已经具备一定的独立思考和探索能力,并能在探索过程中形成自己的观点,能在倾听别人意见的过程中逐渐完善自己的想法.因此,本节课设计了自学和探究活动,给学生提供自主探索与交流的空间,体现知识的形成过程.
三、教学过程:
巧设情境 激发兴趣
在射门游戏中,球员射中球门的难易程度与所处的位置B对球门AC的张角有关。如图,运动员在球门前画了一个圆圈进行无人防守的射门训练。如图,当他站在B,D,E的位置射球时,哪个位置更容易进球?
A
B
C
D
E
思考:图中的∠ABC的顶点各在圆的什么位置?∠ABC的两边和圆是什么关系?
圆心角顶点发生变化时,我们得到几种情况?
A
.
O
B
C
.
思考:三个图中的∠BAC的顶点A各在圆的什么位置?角的两边和圆是什么关系?
.
.
A
O
B
C
A
.
O
B
C
.
讲授新课 探究新知
探究(一)圆周角的定义
B
A
C
A
B
C
D
E
●O
观察图中的∠ABC ,它的顶点在圆上,它的两边分别与圆还有另一个交点.像这样的角,叫做圆周角.
⑵角的两边分别和圆相交
●
注意:
⑴顶点在圆上
●
●
你能仿照圆心角的定义给圆周角下定义吗?
【自测1】请同学们根据定义回答下面问题:在下列与圆有关的角中,哪些是圆周角?哪些不是,为什么?
图1
图2
图3
图4
图5
【自测2】指出图中的圆周角.
A
O
B
C
∠ACO ∠ACB ∠BCO ∠OAB ∠BAC ∠OAC ∠ABO ∠CBO ∠ABC
×
×
√
×
×
【自我检测】
在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.
学科网
探究(二)圆周角和圆心角的关系
活动(一)
做一做
请同学们在圆上确定一条劣弧,画出它所对的圆心角与圆周角。
A
C
O
请你动手画出⊙0中弧AC所对的圆心角和圆周角,观察弧AC所对的圆周角有几个?它们的大小有什么关系?
如图,观察弧AC所对的圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?
说说你的想法,并与同伴交流.
提示:注意圆心与圆周角的位置关系.
A
B
C
●O
A
B
C
●O
●O
A
B
C
圆心在圆周角的一边上
圆心在圆周角的内部
圆心在圆周角的外部
改变圆心角∠AOC的度数,你得到的结论还成立吗?
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
●O
A
B
C
∴∠A=∠B.
∴∠AOC=2∠B.
即 ∠ABC = ∠AOC.
你能写出这个命题吗?
一条弧所对的圆周角等于它所对的圆心角的一半.
活动(二)
议一议
如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
老师提示:能否转化为1的情况?
过点B作直径BD.由1可得:
●O
∴ ∠ABC = ∠AOC.
你能写出这个命题吗?
A
B
C
D
∠ABD = ∠AOD,∠CBD = ∠COD,
一条弧所对的圆周角等于它所对的圆心角的一半.
如果圆心不在圆周角的一边上,结果会怎样?
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
老师提示:能否也转化为1的情况?
过点B作直径BD.由1可得:
●O
∴∠ABC = ∠AOC.
你能写出这个命题吗?
D
∠ABD = ∠AOD,∠CBD = ∠COD,
A
B
C
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即∠ABC= ∠AOC.
D
D
圆心在角的边
圆心在角
圆心在角
上
内
外
定理:
B
A
O
.
70°
x
【自测3】求圆中角x的度数
C
A
O
.
x
120°
A
O
.
120°
C
D
B
【自我检测】
【自测4】如图,已知圆心角∠AOB=100°,求圆周角∠ADB、∠ACB的度数?
【自我检测】
探究(三)圆周角和圆心角的关系
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成的圆周角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?
A
B
C
D
E
圆上一条弧所对的圆周角能做出几个?它们之间有什么关系?
结论:同弧或等弧所对的圆周角相等。
【自测5】试找出下图中所有相等的圆周角。
A
B
C
D
1
2
3
4
5
6
7
8
∠2=∠7
∠1=∠4
∠3=∠6
∠5=∠8
【自我检测】
例1.如图,OA,OB,OC都是⊙O的半径,∠AOB=2∠BOC.则∠ACB与∠BAC的大小有什么关系?为什么?
O
C
A
B
1
2
3
4
解: ∵∠1= ∠3
∠2= ∠4
∠3=2∠4
1
2
__
1
2
__
即∠ACB=2∠BAC
∴∠1=2∠2
答:∠ACB=2∠BAC.
自主学习 合作探究
活动(三)
堂堂测
思考:例2、圆中一条弦所对的圆周角有几个,它们都相等吗?
计算:(1)等于半径的弦对的圆周角 .
(2)半径为R的圆中,有一条弦分圆周成1:2两部分,则弦所对的圆周角的度数是__。
【延伸拓展】
达标检测 及时反馈
1、如图,△ABC内接于⊙O,∠BOC=130°,则∠A的度数为( ).
2、如图,△ABC内接于⊙O,∠ABC=45°,∠ACB=75°,则∠BOC的度数为( ).
3、一条弦分圆为1:4两部分,求这弦所对的圆周角的度数?
4、如图3,有一圆形展厅,在其圆形边缘上的点A处安装了一台监视器,它的监控角度是65°,为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器台.
5、如图5,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则 ∠DCF=__ .
图1
图2
6、拓展练习:
(1)如图,OA、OB、OC都是圆O的半径,
如果:∠AOB=2∠BOC.
求证:∠ACB=2∠BAC
(2)如果∠AOC=100°,则∠ABC=( ).
(3)如果点A、B、C在⊙O中,∠CAB=25°,∠ACB=30°,求弦AC所对圆周角的度数.
课堂小结 知识内化
1、什么是圆周角?它和圆心角有什么不同?
2、圆周角和圆心有几种位置关系?
3、圆周角和圆心角的关系定理是什么?它使用的前提条件是什么?
4、你是如何证明圆周角和圆心角之间的关系的?证明过程中用了哪些数学方法呢?
5、圆周角及圆周角定理的应用极其广泛,也是中考的一个重要考点,望同学们灵活运用.
布置作业 巩固提高
必做题:教材第80至81页第1、2题
选做题:探讨“在同圆或等圆中,相等的弦所对的圆周角的关系”。
