人教版七年级数学下册 5.3平行线的性质 一课一练同步拓展(含答案)
文档属性
| 名称 | 人教版七年级数学下册 5.3平行线的性质 一课一练同步拓展(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 114.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-19 11:25:31 | ||
图片预览

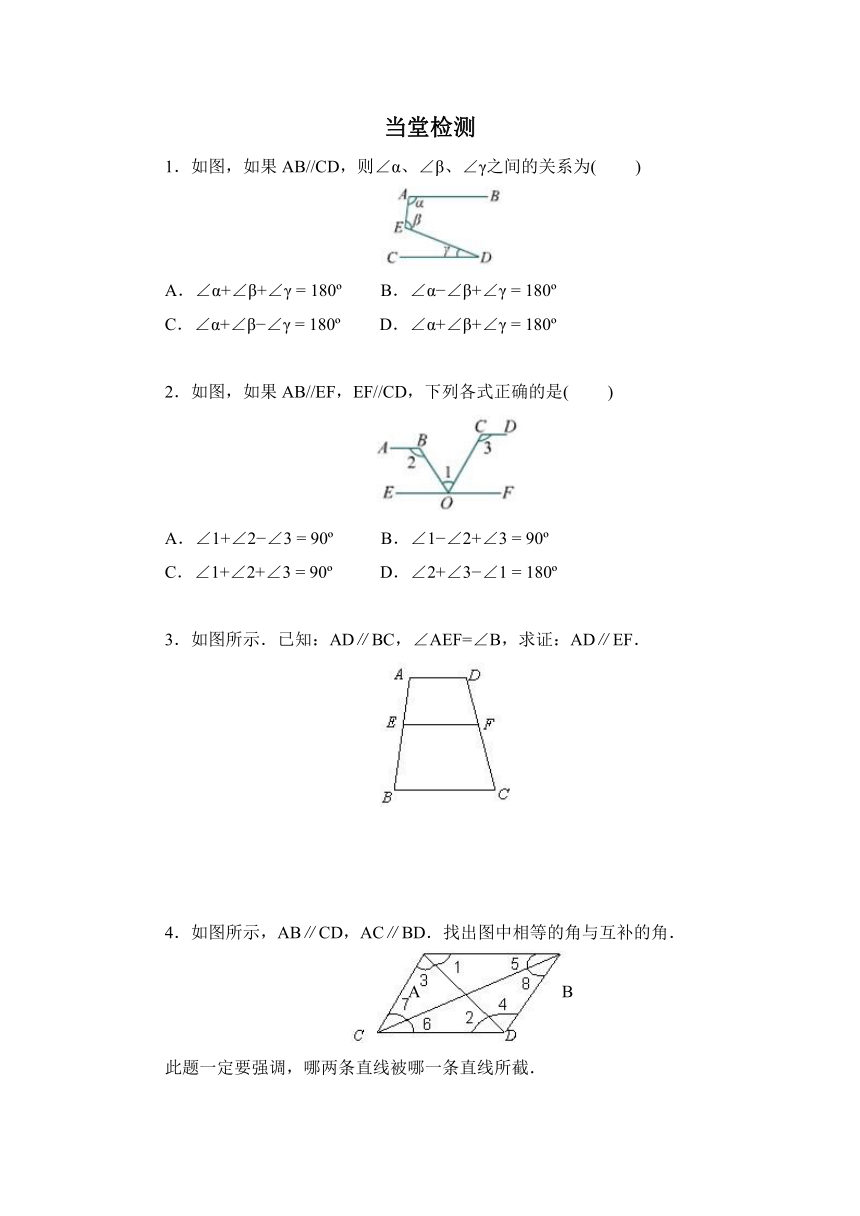
文档简介
5.3平行线的性质
例题1 如图,是梯形中有上底的一部分,已知量得,梯形另外两个角各是多少度?
例题1 解答 因为梯形上、下底互相平行,所以与互补,与互补,于是有.
所以,梯形的另外两个角分别是65°,80°.
例题2 已知,如图,是截线,并且,问直线a与c垂直吗?为什么?
例题2 解答 垂直.理由如下:
(已知),∴(垂直定义),
(已知),∴(两直线平行,同位角相等).
∴(垂直定义).
当堂检测
1.如图,如果AB//CD,则∠α、∠β、∠γ之间的关系为(??????? )
A.∠α+∠β+∠γ = 180? ???????B.∠α?∠β+∠γ = 180?
C.∠α+∠β?∠γ = 180? ???????D.∠α+∠β+∠γ = 180?
2.如图,如果AB//EF,EF//CD,下列各式正确的是(??????? )
A.∠1+∠2?∠3 = 90? ?????????B.∠1?∠2+∠3 = 90?
C.∠1+∠2+∠3 = 90? ?????????D.∠2+∠3?∠1 = 180?
3.如图所示.已知:AD∥BC,∠AEF=∠B,求证:AD∥EF.
4.如图所示,AB∥CD,AC∥BD.找出图中相等的角与互补的角.
此题一定要强调,哪两条直线被哪一条直线所截.
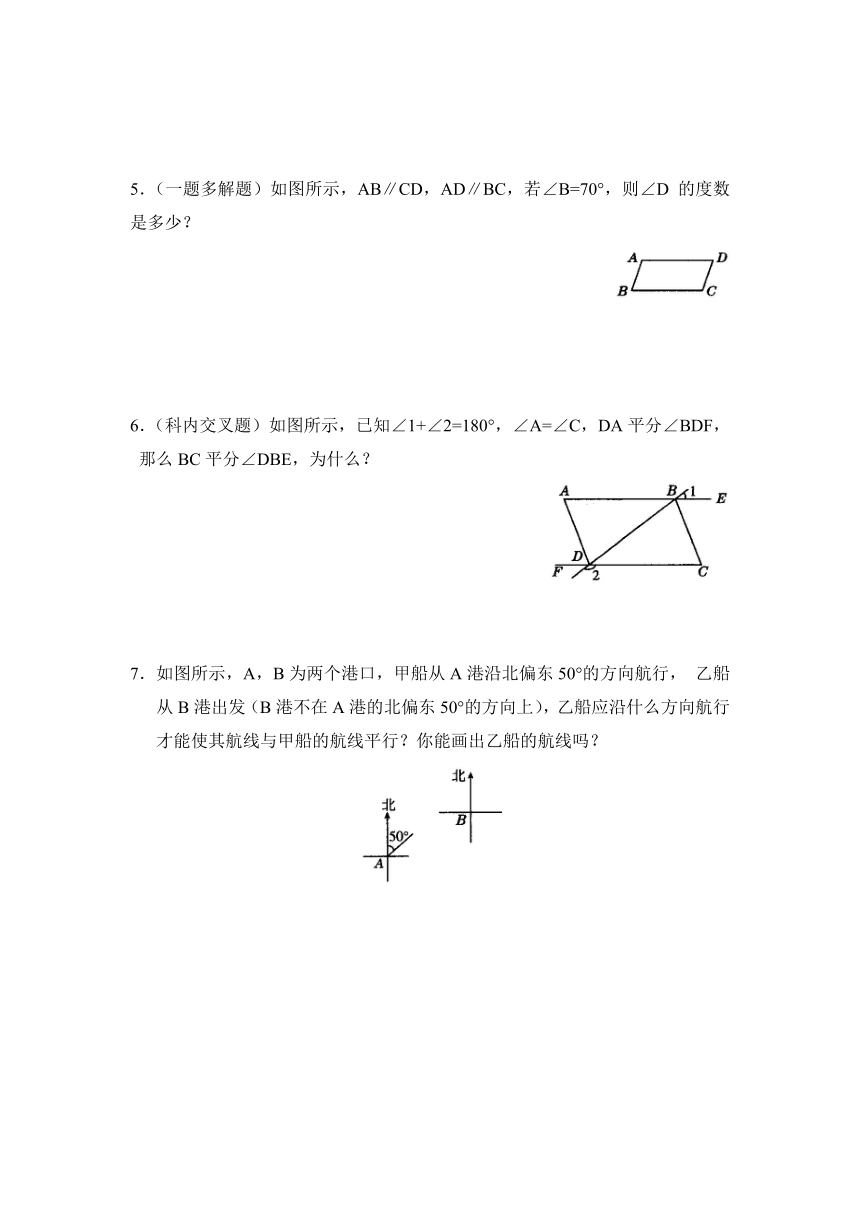
5.(一题多解题)如图所示,AB∥CD,AD∥BC,若∠B=70°,则∠D的度数是多少?
6.(科内交叉题)如图所示,已知∠1+∠2=180°,∠A=∠C,DA平分∠BDF,那么BC平分∠DBE,为什么?
7.如图所示,A,B为两个港口,甲船从A港沿北偏东50°的方向航行,乙船从B港出发(B港不在A港的北偏东50°的方向上),乙船应沿什么方向航行才能使其航线与甲船的航线平行?你能画出乙船的航线吗?
参考答案
1、答案:C
说明:可如图过E点作EF//CD,则∠FED =∠γ;由AB//CD,可知EF//AB,所以∠α+∠AEF = 180?,即∠AEF = 180??∠α;不难看出∠β=∠FED+∠AEF,由此得到∠β=∠γ+∠AEF =∠γ+180??∠α,即∠α+∠β?∠γ= 180?,答案为C.
2、答案:D
说明:由AB//EF,得到∠2 =∠BOF,再由CD//EF,得到∠3+∠COF = 180?,因为∠COF = ∠BOF?∠1,所以有∠3+∠BOF?∠1 = 180?,即∠3+∠2?∠1 = 180?,答案为D.
3、分析:(执果索因)从图直观分析,欲证AD∥EF,只需∠A+∠AEF=180°,
(由因求果)因为AD∥BC,所以∠A+∠B=180°,又∠B=∠AEF,所以∠A+∠AEF=180°成立.于是得证.
证明:因为? AD∥BC,(已知)
所以? ∠A+∠B=180°.(两直线平行,同旁内角互补)
因为? ∠AEF=∠B,(已知)
所以? ∠A+∠AEF=180°,(等量代换)
所以? AD∥EF.(同旁内角互补,两条直线平行)
4、答:相等的角为:∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8.互补的角为:∠BAC+∠ACD=180°,∠ABD+∠CDB=180°,∠CAB+∠DBA=180°,∠ACD+∠BDC=180°.
相等的角还有:∠ACD=∠ABD,∠BAC=∠BDC.(同角的补角相等)
5.解法一:因为AB∥CD,AD∥BC(已知),
所以∠B+∠C=180°,∠C+∠D=180°(两直线平行,同旁内角互补),
所以∠D=∠B(同角的补角相等),又∠B=70°,所以∠D°=70°.
解法二:如答图所示,连接BD,因为AB∥CD(已知),
所以∠1=∠2(两直线平行,内错角相等).因为AD∥BC(已知),
所以∠3=∠4(两直线平行,内错角相等),
所以∠1+∠4=∠2+∠3(等式性质),即∠ABC=∠ADC,
因为∠ABC=70°,所以∠ADC=70°.
解法三:如图所示,延长BC到点E,因为AB∥CD(已知),
所以∠B=∠DCE(两直线平行,同位角相等),
因为AD∥BC(已知),
所以∠D=∠DCE(两直线平行,内错角相等),
所以∠D=∠B(等量代换),因为∠B=70°,所以∠D=70°.
点拨:添加辅助线可以帮助解题,而辅助线的作法不一定是惟一的,很多民政部下可有多种作法.
6.解:因为∠2+∠BDC=180°,又因为∠2+∠1=180°(已知),
所以∠BDC=∠1,所以AE∥FC(同位角相等,两直线平行),
所以∠EBC=∠C(两直线平行,内错角相等).
又因为∠A=∠C(已知),
所以∠EBC=∠A(等量代换),
所以AD∥BC(同位角相等,两直线平行),
所以∠ADB=∠ADF,所以∠EBC=∠DBC(等量代换),
所以BC平分∠DBE(角平分线的概念).
7.解:本题有两种情况,如图(1),(2)所示.
在图(1)中,因为AC∥BD,所以∠1=∠3=50°,
又因为AD∥BE,所以∠2=∠3=50°,
所以乙船沿北偏东50°的方向航行,航线如图(1)中BE;
在图(2)中,因为AC∥BD,
所以∠1=∠3,而AD∥BE,所以∠2=∠3=50°,
所以乙船沿南偏西50°的方向航行,航线如图(2)中BE.
B
A
