9.4 矩形、菱形、正方形学案(无答案)
文档属性
| 名称 | 9.4 矩形、菱形、正方形学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 228.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-20 00:00:00 | ||
图片预览



文档简介
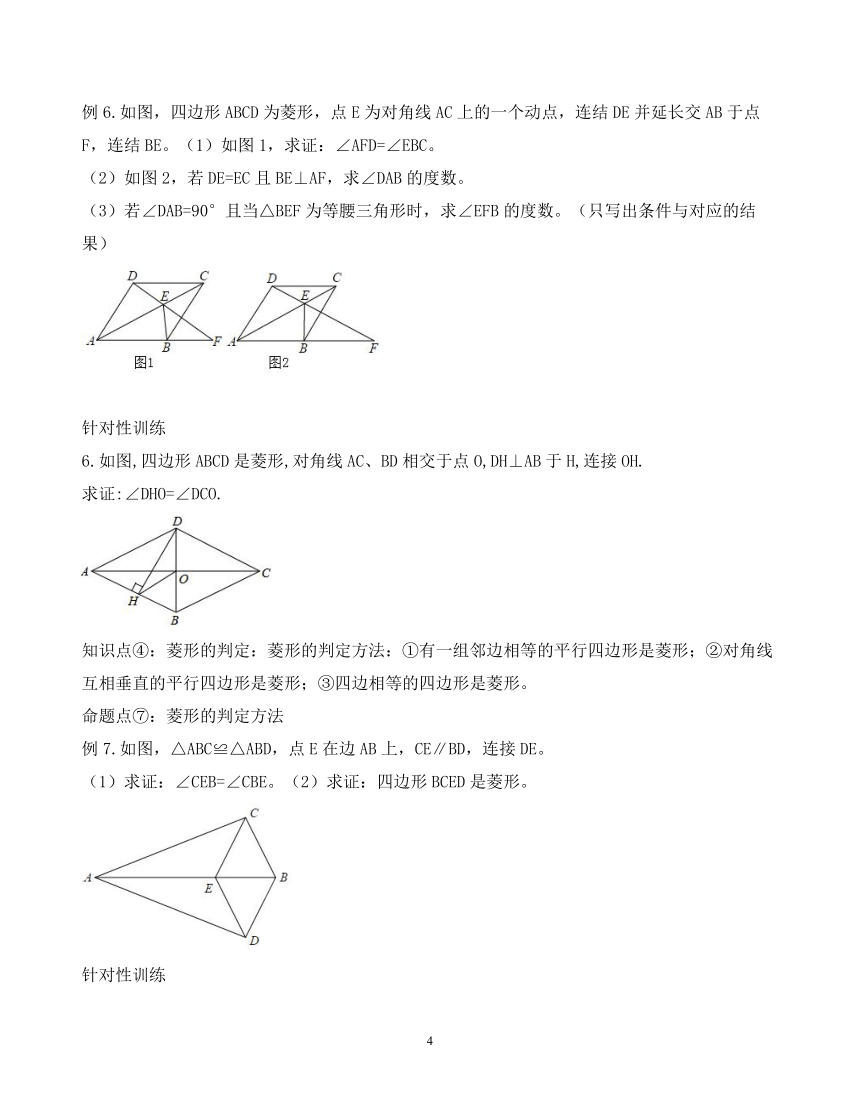
矩形,菱形,正方形 知识点一:矩形定义及性质 1.矩形的定义:有一个角是直角的平行四边形叫做矩形,矩形也叫长方形。 2.矩形的性质:(1)对称性:矩形是中心对称图形也是轴对称图形。(2)边:对边相等且平行。(3)角:四个角都是直角。(4)对角线:对角线相等且互相平分。 命题点①:矩形中的计算 例1:如图,已知矩形的对角线AC与BD相交于点O,若AO=1,那么BD=????. 针对性训练 1.如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为?? ? ? ? ? ?。 命题点②:运用矩形的性质证明相等关系 例2:如图,在矩形ABCD中,BF=CE。求证:AE=DF。 针对性训练 2.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF。求证:OE=OF。 知识点2:矩形的判定 矩形的判定:①有一个角是直角的平行四边形叫做矩形;②对角线相等的平行四边形是矩形;③三个角是直角的四边形是矩形。 命题点③:矩形的判定方法 例3:如图,在中,,点D(不与点B重合)在BC上,点E是AB的中点,过点A作AF∥BC交DE延长线于点F,连接AD,BF。: (1)求证:。 (2)若BD=CD,求证:四边形AFBD是矩形。 针对性训练 3.已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC。 ①求证:CD=AN。②若∠AMD=2∠MCD,求证:四边形ADCN是矩形。 命题点④:添加条件构造矩形 例4.如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.当点O运动到何处时,四边形AECF是矩形? 并证明你的结论.?
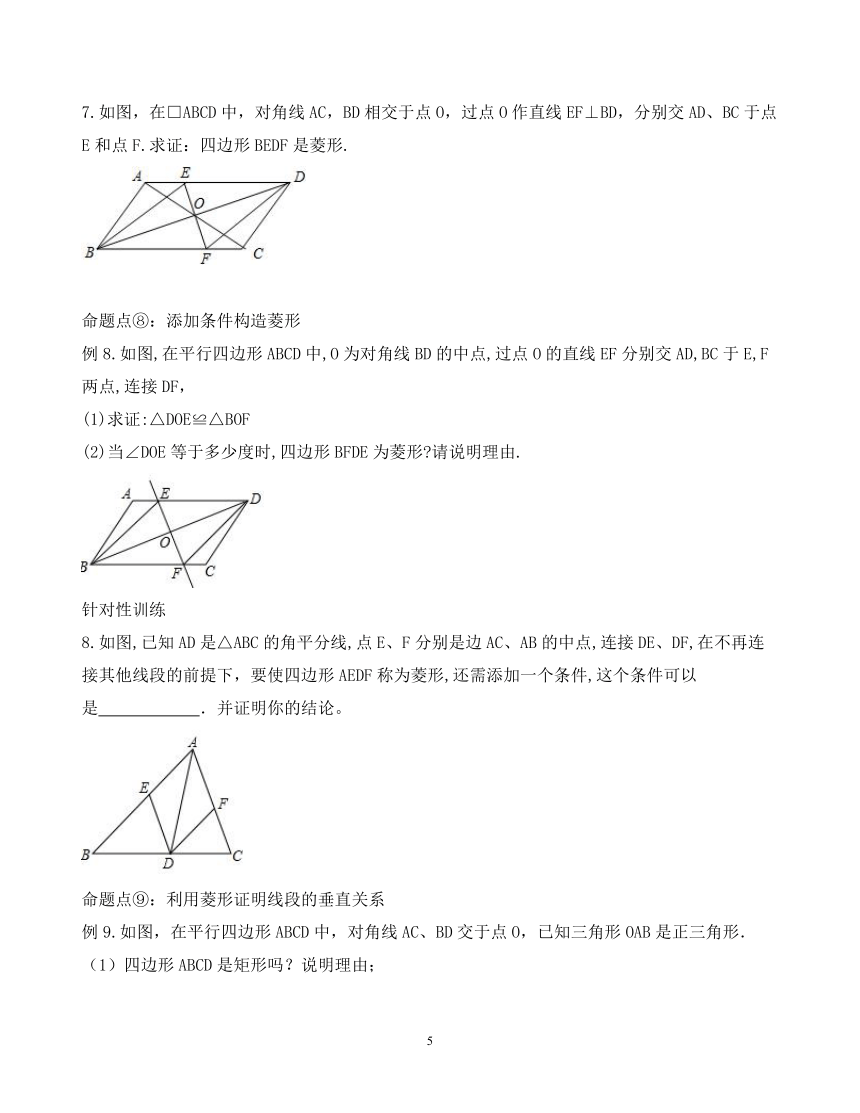
针对性训练 4.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF。 (1)线段BD与CD有何数量关系,为什么?。 (2)当△ABC满足什么条件时,四边形AFBD是矩形?,请说明理由。 知识点3:菱形的定义及性质 1.菱形的定义:有一组邻边相等的平行四边形叫做菱形。 2.菱形的性质:(1)对称性:菱形是中心对称图形也是轴对称图形。(2)边:四边相等且对边平行。 (3)角:对角相等。(4)对角线:互相垂直平分。 命题点⑤:菱形中的计算 例5.如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于(??) A.3.5????? B.4????? C.7????? D.14 针对性训练 5.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO。若∠DAC=28°,则∠OBC的度数为(??)。 A.28° B.52° C.62° D.72° 命题点⑥:运用菱形的性质进行证明 例6.如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连结DE并延长交AB于点F,连结BE。(1)如图1,求证:∠AFD=∠EBC。 (2)如图2,若DE=EC且BE⊥AF,求∠DAB的度数。 (3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数。(只写出条件与对应的结果) 针对性训练 6.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH. 求证:∠DHO=∠DCO. 知识点④:菱形的判定:菱形的判定方法:①有一组邻边相等的平行四边形是菱形;②对角线互相垂直的平行四边形是菱形;③四边相等的四边形是菱形。 命题点⑦:菱形的判定方法 例7.如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE。 (1)求证:∠CEB=∠CBE。(2)求证:四边形BCED是菱形。 针对性训练 7.如图,在□ABCD中,对角线AC,BD相交于点O,过点O作直线EF⊥BD,分别交AD、BC于点E和点F.求证:四边形BEDF是菱形. 命题点⑧:添加条件构造菱形 例8.如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连接DF,
(1)求证:△DOE≌△BOF
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由. 针对性训练 8.如图,已知AD是△ABC的角平分线,点E、F分别是边AC、AB的中点,连接DE、DF,在不再连接其他线段的前提下,要使四边形AEDF称为菱形,还需添加一个条件,这个条件可以是 .并证明你的结论。 命题点⑨:利用菱形证明线段的垂直关系 例9.如图,在平行四边形ABCD中,对角线AC、BD交于点O,已知三角形OAB是正三角形.?
(1)四边形ABCD是矩形吗?说明理由;?
(2)若AE∥BD,DE∥AC,求证:OE⊥AD. 针对性训练 9.如图,矩形ABCD的对角线相交于点O,过点O的直线EF与AB、CD的延长线分别交于点E、F.
(1)探索线段OE和OF的大小关系并说明理由;
(2)当EF与AC满足什么条件时,四边形AECF是菱形?请说明理由. 知识点5:正方形定义及性质 1.正方形的概念:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。 2.正方形的性质:正方形既是矩形又是菱形,它具有矩形和菱形的全部性质。 命题点⑩:正方形中的计算 例10.如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC于点E,将△BCE绕点C顺时针旋转90°得到△DCF,若CE=1cm,则BF=_____cm。 针对性训练 10.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为?? ? ? ? ? ?。 (例11图) 命题点?:运用正方形的性质证明相等关系 例11.已知,如图,正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF,连接DE、DF。求证:DE=DF。 针对性训练 11.如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G。 (1)求证:AE=CF。 (2)若∠ABE=55°,求∠EGC的大小。 命题点?:正方形的判定 例12.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上点.过点P作PM⊥AD,PN⊥CD,垂足分别为点M、N. (1)求证:∠ADB=∠CDB; (2)若∠ADC=90°,求证:四边形MPND是正方形. 针对性训练 12.如图,在△ABC中,点D是边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE.
(1)求证:DE=DF;(2)当∠A=90°时,试判断四边形AFDE是怎样的四边形,并证明你的结论. 命题点?:添加条件构造正方形 例13.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E。(1)求证:四边形ADCE为矩形。(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明。 针对性训练 13.已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E。(1)求证:△AOD≌△EOC。(2)连接AC,DE,当∠B=∠AEB_____时,四边形ACED是正方形?请说明理由。 多维解题方略 类型题:线段之和最短问题 例:如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为(??)。 A:? B:? C:? D:? 针对性训练 如图,正方形ABCD的边长为4,点P在DC边上且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为?? ? ? ? ? ?。 易错易混警示 易错点:混淆平行四边形、矩形、菱形及正方形的性质 例:正方形具有而菱形不一定具有的性质是( ) A.对角线互相垂直平分B.内角和为360°C.对角线相等D.对角线平分内角 得分高手体验: 例:如图,正方形ABCD内有一个内接△AEF,若∠EAF=45°,AB=8厘米,EF=7厘米,则△EFC的面积是 . 针对性训练 在四边形ABCD中,∠A=60°,∠ABC=∠ADC=90°,BC=2,CD=11,自D作DH⊥AB于H,则DH的长是(?)
A.?7.5 B.?7 C.?6.5 D.?5.5 【课后作业】 1.如图所示,甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形。则(??)。 A: 甲、乙都可以 B: 甲、乙都不可以 C: 甲不可以,乙可以 D: 甲可以,乙不可以 2.下列命题是真命题的是( ?)。 A: 对角线互相平分的四边形是平行四边形 B: 对角线相等的四边形是矩形 C: 对角线互相垂直的四边形是菱形 D: 对角线互相垂直的四边形是正方形 3.边长为3cm的菱形的周长是(??)。 A:?6cm B:?9cm C:?12cm D:?15cm 4.如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,。以上结论中,你认为正确的有(??)个。 A:?1 B:?2 C:?3 D:?4 5.已知菱形ABCD的面积为24cm?,若对角线AC=6cm,则这个菱形的边长为? ? ? ?cm。 6.如果菱形的两条对角线的长为a和b,且a,b满足,那么菱形的面积等于?? ? ?。 7.如图所示,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥EC;③AB=AC。从中选择一个条件使四边形BECF是菱形,并给出证明,你选择的条件是_____(只填写序号)。 8.如图,矩形ABCD的面积为20cm?,对角线交于点O;以AB、AO为邻边作平行四边形,对角线交于点;以AB、为邻边作平行四边形;;依此类推,则平行四边形的面积为 . 9.如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是为E,F,并且DE=DF. (1)求证:△AED≌△CFD; (2)求证:四边形ABCD是菱形. 10.如图,在正方形中,BE=DF (1)求证:CE=CF。 (2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么? 11.如图,E是矩形ABCD边BC的中点,P是AD边上一动点,PF⊥AE,PH⊥DE,垂足分别为F,H.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PHEF是矩形?请予以证明;
(2)在(1)中,动点P运动到什么位置时,矩形PHEF变为正方形?为什么?
12.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F。 (1)证明:PC=PE。 (2)求∠CPE的度数。 (3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由。
12
针对性训练 4.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF。 (1)线段BD与CD有何数量关系,为什么?。 (2)当△ABC满足什么条件时,四边形AFBD是矩形?,请说明理由。 知识点3:菱形的定义及性质 1.菱形的定义:有一组邻边相等的平行四边形叫做菱形。 2.菱形的性质:(1)对称性:菱形是中心对称图形也是轴对称图形。(2)边:四边相等且对边平行。 (3)角:对角相等。(4)对角线:互相垂直平分。 命题点⑤:菱形中的计算 例5.如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于(??) A.3.5????? B.4????? C.7????? D.14 针对性训练 5.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO。若∠DAC=28°,则∠OBC的度数为(??)。 A.28° B.52° C.62° D.72° 命题点⑥:运用菱形的性质进行证明 例6.如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连结DE并延长交AB于点F,连结BE。(1)如图1,求证:∠AFD=∠EBC。 (2)如图2,若DE=EC且BE⊥AF,求∠DAB的度数。 (3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数。(只写出条件与对应的结果) 针对性训练 6.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH. 求证:∠DHO=∠DCO. 知识点④:菱形的判定:菱形的判定方法:①有一组邻边相等的平行四边形是菱形;②对角线互相垂直的平行四边形是菱形;③四边相等的四边形是菱形。 命题点⑦:菱形的判定方法 例7.如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE。 (1)求证:∠CEB=∠CBE。(2)求证:四边形BCED是菱形。 针对性训练 7.如图,在□ABCD中,对角线AC,BD相交于点O,过点O作直线EF⊥BD,分别交AD、BC于点E和点F.求证:四边形BEDF是菱形. 命题点⑧:添加条件构造菱形 例8.如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连接DF,
(1)求证:△DOE≌△BOF
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由. 针对性训练 8.如图,已知AD是△ABC的角平分线,点E、F分别是边AC、AB的中点,连接DE、DF,在不再连接其他线段的前提下,要使四边形AEDF称为菱形,还需添加一个条件,这个条件可以是 .并证明你的结论。 命题点⑨:利用菱形证明线段的垂直关系 例9.如图,在平行四边形ABCD中,对角线AC、BD交于点O,已知三角形OAB是正三角形.?
(1)四边形ABCD是矩形吗?说明理由;?
(2)若AE∥BD,DE∥AC,求证:OE⊥AD. 针对性训练 9.如图,矩形ABCD的对角线相交于点O,过点O的直线EF与AB、CD的延长线分别交于点E、F.
(1)探索线段OE和OF的大小关系并说明理由;
(2)当EF与AC满足什么条件时,四边形AECF是菱形?请说明理由. 知识点5:正方形定义及性质 1.正方形的概念:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。 2.正方形的性质:正方形既是矩形又是菱形,它具有矩形和菱形的全部性质。 命题点⑩:正方形中的计算 例10.如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC于点E,将△BCE绕点C顺时针旋转90°得到△DCF,若CE=1cm,则BF=_____cm。 针对性训练 10.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为?? ? ? ? ? ?。 (例11图) 命题点?:运用正方形的性质证明相等关系 例11.已知,如图,正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF,连接DE、DF。求证:DE=DF。 针对性训练 11.如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G。 (1)求证:AE=CF。 (2)若∠ABE=55°,求∠EGC的大小。 命题点?:正方形的判定 例12.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上点.过点P作PM⊥AD,PN⊥CD,垂足分别为点M、N. (1)求证:∠ADB=∠CDB; (2)若∠ADC=90°,求证:四边形MPND是正方形. 针对性训练 12.如图,在△ABC中,点D是边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE.
(1)求证:DE=DF;(2)当∠A=90°时,试判断四边形AFDE是怎样的四边形,并证明你的结论. 命题点?:添加条件构造正方形 例13.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E。(1)求证:四边形ADCE为矩形。(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明。 针对性训练 13.已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E。(1)求证:△AOD≌△EOC。(2)连接AC,DE,当∠B=∠AEB_____时,四边形ACED是正方形?请说明理由。 多维解题方略 类型题:线段之和最短问题 例:如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为(??)。 A:? B:? C:? D:? 针对性训练 如图,正方形ABCD的边长为4,点P在DC边上且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为?? ? ? ? ? ?。 易错易混警示 易错点:混淆平行四边形、矩形、菱形及正方形的性质 例:正方形具有而菱形不一定具有的性质是( ) A.对角线互相垂直平分B.内角和为360°C.对角线相等D.对角线平分内角 得分高手体验: 例:如图,正方形ABCD内有一个内接△AEF,若∠EAF=45°,AB=8厘米,EF=7厘米,则△EFC的面积是 . 针对性训练 在四边形ABCD中,∠A=60°,∠ABC=∠ADC=90°,BC=2,CD=11,自D作DH⊥AB于H,则DH的长是(?)
A.?7.5 B.?7 C.?6.5 D.?5.5 【课后作业】 1.如图所示,甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形。则(??)。 A: 甲、乙都可以 B: 甲、乙都不可以 C: 甲不可以,乙可以 D: 甲可以,乙不可以 2.下列命题是真命题的是( ?)。 A: 对角线互相平分的四边形是平行四边形 B: 对角线相等的四边形是矩形 C: 对角线互相垂直的四边形是菱形 D: 对角线互相垂直的四边形是正方形 3.边长为3cm的菱形的周长是(??)。 A:?6cm B:?9cm C:?12cm D:?15cm 4.如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,。以上结论中,你认为正确的有(??)个。 A:?1 B:?2 C:?3 D:?4 5.已知菱形ABCD的面积为24cm?,若对角线AC=6cm,则这个菱形的边长为? ? ? ?cm。 6.如果菱形的两条对角线的长为a和b,且a,b满足,那么菱形的面积等于?? ? ?。 7.如图所示,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥EC;③AB=AC。从中选择一个条件使四边形BECF是菱形,并给出证明,你选择的条件是_____(只填写序号)。 8.如图,矩形ABCD的面积为20cm?,对角线交于点O;以AB、AO为邻边作平行四边形,对角线交于点;以AB、为邻边作平行四边形;;依此类推,则平行四边形的面积为 . 9.如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是为E,F,并且DE=DF. (1)求证:△AED≌△CFD; (2)求证:四边形ABCD是菱形. 10.如图,在正方形中,BE=DF (1)求证:CE=CF。 (2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么? 11.如图,E是矩形ABCD边BC的中点,P是AD边上一动点,PF⊥AE,PH⊥DE,垂足分别为F,H.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PHEF是矩形?请予以证明;
(2)在(1)中,动点P运动到什么位置时,矩形PHEF变为正方形?为什么?
12.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F。 (1)证明:PC=PE。 (2)求∠CPE的度数。 (3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由。
12
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
