人教版四年级下册数学课件:10 总复习 第3课时 图形与几何 (共27张PPT)
文档属性
| 名称 | 人教版四年级下册数学课件:10 总复习 第3课时 图形与几何 (共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-19 20:18:33 | ||
图片预览






文档简介
(共27张PPT)
第3课时 图形与几何
我发现从不同方向观察同一个立体图形,看到的形状可能是不同的;从同一方向观察不同的立体图形,看到的形状可能是相同的。
我会给三角形画高,还会按不同标准给三角形分类。
我知道了所有三角形的内角和都是180°,我还知道三角形任意两边的和一定大于第三边。
我会画轴对称图形,还会将一个图形向上、下、左、右方向平移。
你能用自己喜欢的方式把第五单元三角形这部分知识整理一下吗?
单元 知识点 具体内容
第
五
单
元
:
三
角
形 三角形的定义 由3条线段围成的图形(每相邻两条线段的端点相
连)叫做三角形。
三角形的高和底 从三角形的一个顶点到它的对边作一条垂线,顶点
和垂足之间的线段叫做三角形的高,这条对边叫做
三角形的底。
三角形的特性 三角形具有稳定性。
三角形三边的关系 三角形任意两边的和大于第三边。
三角形的分类 按角分类:锐角三角形、直角三角形和钝角三角形。按边分类:不等边三角形和等腰三角形(等边三角
形是特殊的等腰三角形)。
三角形的内角和 三角形的内角和是180°。
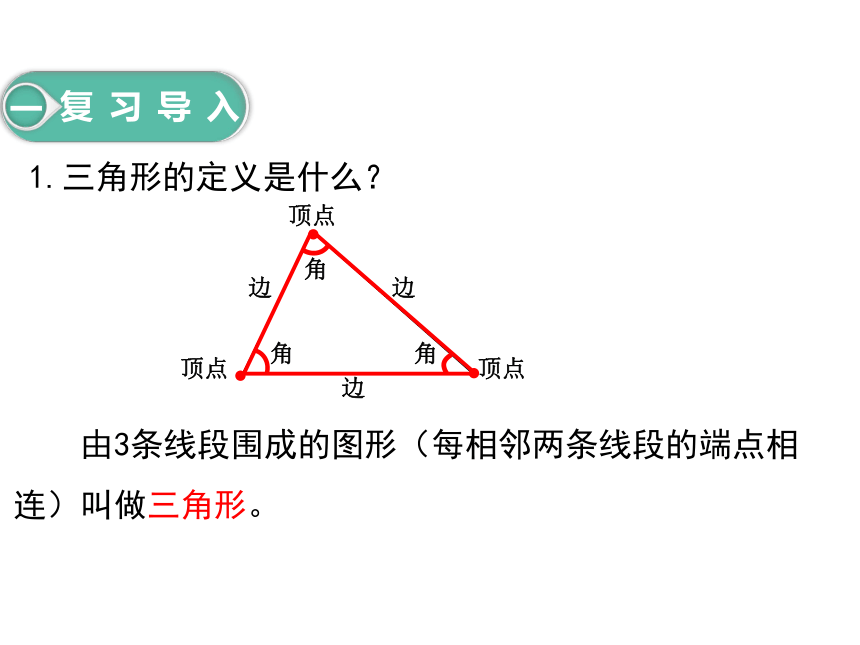
1.三角形的定义是什么?
由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
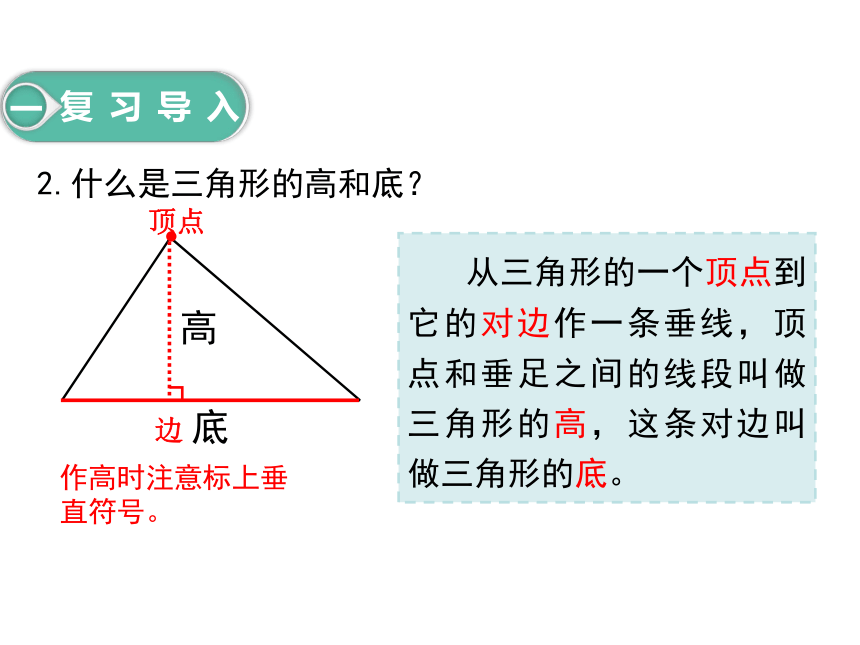
2.什么是三角形的高和底?
从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。
高
底
顶点
边
作高时注意标上垂直符号。
3.三角形有什么特性?
稳定性。
4.三角形的三边、三角有什么关系?
三角形任意两边的和大于第三边。三角形的三个内角和是180°。
三角形按边分类:
三角形按角分类:
5.三角形可以怎么分类?
6.什么样的图形是轴对称图形?它有什么性质?
像这样,对折后两边能够完全重合的图形就是轴对称图形。
中间这条直线就是对称轴。
对应点到对称轴的距离相等;对应点的连线垂直于对称轴。
7.怎样画轴对称图形的对称轴和轴对称图形的另一半呢?
第一步:找到关键点;
第二步:通过数格找到对称点;
A
5格
5格
B'
B
3格
3格
第三步:顺次连线。
1. 求下面各角的度数。
2.如果一个三角形的两条边分别是4cm和7cm,另一条边可能是几厘米(取整厘米数)?
4+7=11(cm)
3+4=7(cm)
3cm<第三条边<11cm
答:另一条边可能是4cm或5cm或6cm
或7cm或8cm或9cm或10cm。
3.
4.
5.
3×2=6(cm2)
6.
7.
8. 连一连。
9. 在( )里填上适当的数或文字。
(1)小明准备用图钉固定硬纸条做一个三角形。他应该准备( )根硬纸条,因为三角形有( )条边,他应该准备( )个图钉,因为三角形有三个( )。
3
3
3
顶点
(2)红领巾按角分类属于( )三角形,按边分
类属于( )三角形。
钝角
等腰
(3)等边三角形的每个内角都是( )°,等腰直
角三角形的一个底角是( )° 。
60
(4)房屋的屋架做成三角形是运用了三角形的( )。
稳定性
45
AC
AD
10. 下面的说法正确吗?正确的画“√”,错误的画“×”。
(1)在一个三角形中,如果有两个锐角,那么这个三 角形就一定是锐角三角形。 ( )
×
(2)钝角三角形只有一条高。 ( )
×
(3)锐角三角形中任意两个锐角的和一定大于90°。
( )
√
(4)把一个大三角形剪成两个小三角形,每个小三角形的内角和是 90°。 ( )
×
(5)一个等腰三角形的周长是21厘米,底边长是3厘米,则腰长是 9厘米。 ( )
√
(6)有一个角是60°的等腰三角形一定是一个等边三角形 。 ( )
√
√
√
√
√
√
√
√
11.
12. 准备若干个边长为1cm的等边三角形,并按下图所示一个接一个地拼摆起来,然后填写下表。
1
3
2
4
3
5
4
6
5
7
6
8
7
9
8
10
12
102
第3课时 图形与几何
我发现从不同方向观察同一个立体图形,看到的形状可能是不同的;从同一方向观察不同的立体图形,看到的形状可能是相同的。
我会给三角形画高,还会按不同标准给三角形分类。
我知道了所有三角形的内角和都是180°,我还知道三角形任意两边的和一定大于第三边。
我会画轴对称图形,还会将一个图形向上、下、左、右方向平移。
你能用自己喜欢的方式把第五单元三角形这部分知识整理一下吗?
单元 知识点 具体内容
第
五
单
元
:
三
角
形 三角形的定义 由3条线段围成的图形(每相邻两条线段的端点相
连)叫做三角形。
三角形的高和底 从三角形的一个顶点到它的对边作一条垂线,顶点
和垂足之间的线段叫做三角形的高,这条对边叫做
三角形的底。
三角形的特性 三角形具有稳定性。
三角形三边的关系 三角形任意两边的和大于第三边。
三角形的分类 按角分类:锐角三角形、直角三角形和钝角三角形。按边分类:不等边三角形和等腰三角形(等边三角
形是特殊的等腰三角形)。
三角形的内角和 三角形的内角和是180°。
1.三角形的定义是什么?
由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
2.什么是三角形的高和底?
从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。
高
底
顶点
边
作高时注意标上垂直符号。
3.三角形有什么特性?
稳定性。
4.三角形的三边、三角有什么关系?
三角形任意两边的和大于第三边。三角形的三个内角和是180°。
三角形按边分类:
三角形按角分类:
5.三角形可以怎么分类?
6.什么样的图形是轴对称图形?它有什么性质?
像这样,对折后两边能够完全重合的图形就是轴对称图形。
中间这条直线就是对称轴。
对应点到对称轴的距离相等;对应点的连线垂直于对称轴。
7.怎样画轴对称图形的对称轴和轴对称图形的另一半呢?
第一步:找到关键点;
第二步:通过数格找到对称点;
A
5格
5格
B'
B
3格
3格
第三步:顺次连线。
1. 求下面各角的度数。
2.如果一个三角形的两条边分别是4cm和7cm,另一条边可能是几厘米(取整厘米数)?
4+7=11(cm)
3+4=7(cm)
3cm<第三条边<11cm
答:另一条边可能是4cm或5cm或6cm
或7cm或8cm或9cm或10cm。
3.
4.
5.
3×2=6(cm2)
6.
7.
8. 连一连。
9. 在( )里填上适当的数或文字。
(1)小明准备用图钉固定硬纸条做一个三角形。他应该准备( )根硬纸条,因为三角形有( )条边,他应该准备( )个图钉,因为三角形有三个( )。
3
3
3
顶点
(2)红领巾按角分类属于( )三角形,按边分
类属于( )三角形。
钝角
等腰
(3)等边三角形的每个内角都是( )°,等腰直
角三角形的一个底角是( )° 。
60
(4)房屋的屋架做成三角形是运用了三角形的( )。
稳定性
45
AC
AD
10. 下面的说法正确吗?正确的画“√”,错误的画“×”。
(1)在一个三角形中,如果有两个锐角,那么这个三 角形就一定是锐角三角形。 ( )
×
(2)钝角三角形只有一条高。 ( )
×
(3)锐角三角形中任意两个锐角的和一定大于90°。
( )
√
(4)把一个大三角形剪成两个小三角形,每个小三角形的内角和是 90°。 ( )
×
(5)一个等腰三角形的周长是21厘米,底边长是3厘米,则腰长是 9厘米。 ( )
√
(6)有一个角是60°的等腰三角形一定是一个等边三角形 。 ( )
√
√
√
√
√
√
√
√
11.
12. 准备若干个边长为1cm的等边三角形,并按下图所示一个接一个地拼摆起来,然后填写下表。
1
3
2
4
3
5
4
6
5
7
6
8
7
9
8
10
12
102
