初中数学华师大版七下第六、七章教材分析 课件(36张PPT)
文档属性
| 名称 | 初中数学华师大版七下第六、七章教材分析 课件(36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-19 13:30:56 | ||
图片预览







文档简介
课件36张PPT。方程小天地
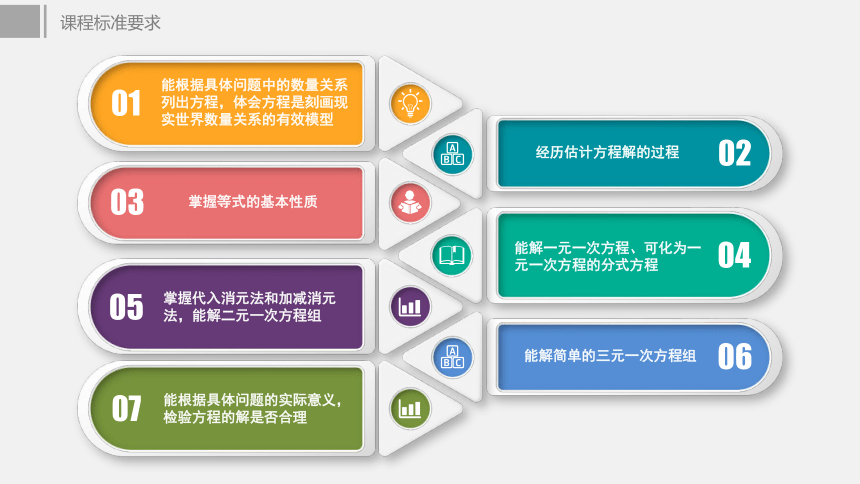
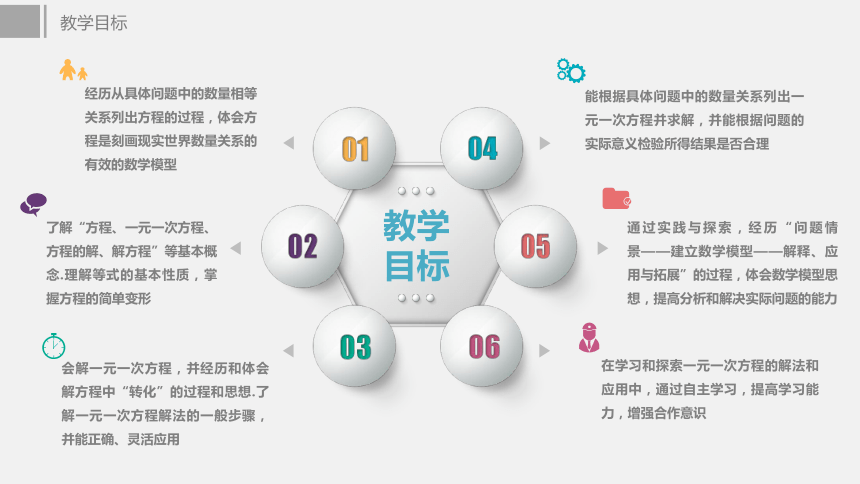
次元大文章知识结构重要性一元一次方程经历从具体问题中的数量相等关系列出方程的过程,体会方程是刻画现实世界数量关系的有效的数学模型了解“方程、一元一次方程、方程的解、解方程”等基本概念.理解等式的基本性质,掌握方程的简单变形会解一元一次方程,并经历和体会解方程中“转化”的过程和思想.了解一元一次方程解法的一般步骤,并能正确、灵活应用在学习和探索一元一次方程的解法和应用中,通过自主学习,提高学习能力,增强合作意识通过实践与探索,经历“问题情景——建立数学模型——解释、应用与拓展”的过程,体会数学模型思想,提高分析和解决实际问题的能力能根据具体问题中的数量关系列出一元一次方程并求解,并能根据问题的实际意义检验所得结果是否合理教学
目标6.3 实践与探索复习6.1 从实际问题到方程6.2 解一元一次方程体会设元之后在思维、列式上直接明了的优点尝试检验法,寻求答案,引导学生学会检验解的正确性有效利用课标例题,
感受以上学习内容等式的基本性质方程的变形规则??一元一次方程:
只含有一个未知数,且所含未知数的式子都是整式,未知数的次数为1,这样的方程叫做一元一次方程。判断下列那些是一元一次方程:
(1) (2)
(3) (4)
(5) (6)
(7) (8)去括号时注意去括号法则注意:1.分数线有括号的作用
2.等式的基本性质0102030405去分母时分数线有括号的作用;不要漏乘不含分母的项括号前面是负号,去括号时注意括号内各项要改变符号移项时要变号将字母前的系数相加减,与字母和字母的指数无关乘以未知数系数的
倒数(除以未知数的系数)方程的变形规则2去括号法则方程的变形规则1合并同类项法则方程的变形规则2依据注意列表用代数式表示相关量分析等量关系画图用代数式表示相关量分析等量关系体会不同设元方法,根据题意合理、灵活地设元提出问题解决问题变式一
甲、乙两站相距162km,一列慢车从甲站开出,时速为36km;一列快车从乙站开出,时速48km,按照下列各情况列出方程。 (1) 两车同时开出相向而行,________h后相遇; (2) 慢车先开出1h,相向而行,快车开出_______h后两车相遇; (3) 两列火车同时开出,相背而行,________h后相距280km; (4) 两列火车同时同向而行,快车在慢车后面,________小时后可以追上慢车; (5) 快车先开出1小时,同向而行,快车在慢车后面,快车开出________小时后可追上慢车。变式二
甲、乙两人在环形跑道上练习跑步,已知环形跑道一圈长400米,乙每秒跑6米,甲每秒跑8米.
(1) 如果甲、乙两人在跑道上相距8米处同时反向出发,那么经过多少秒两人首次相遇?
(2) 如果甲在乙前面8米处同时同向出发,那么经过多少秒两人首次相遇?变式三
如图,两人沿着边长为90m的正方形行走,按A→B→C→D→A…方向,甲从A以65m/min的速度,乙从B以72m/min的速度行走,当乙第一次追上甲时,在正方形的哪一条边上?在应用一元一次方程解实际问题时,要学会分析问题的本领.能根据题意,将实际问题转化为数学问题,特别是寻求主要的数量相等关系,列出方程.求得方程的解后,要注意检验所得结果是否符合实际问题的要求.对一元一次方程的认识,要联系生活实际,在解决实际问题过程中体会:方程是反映现实世界数量相等关系的一个有效的数学模型.解一元一次方程时,既要注意合理地进行方程的变形,也要注意根据方程的特点灵活运用方程的变形规则.010302一次方程组掌握代入消元法和加减消元法,能解二元一次方程组通过列出一次方程组解决有多个未知数的实际问题,理解一次方程组及其解的基本概念,进一步体会方程和方程组是刻画现实世界数量关系的有效模型01*0302能解简单的三元一次方程组通过探求一次方程组的解法,经历从二元一次方程组到一元一次方程转化的过程.体会“消元”和“化归”的数学思想方法0405会根据实际问题中的数量关系列出一次方程组并求解,能检验所得结果是否符合题意0203042课时057.2 二元一次方程组的解法*7.3 三元一次方程组及其解法7.4 实践与探索复习012课时2课时5课时7.1 二元一次方程组和它的解1课时将二元转化为一元,概括代入消元法的基本方法和步骤由简到难,进一步体会“化归”思想在实际问题中,经常会遇到有多个未知量的问题.和一元一次方程一样,二(三)元一次方程组也是反映现实世界数量之间相等关系的数学模型.要学会将实际问题转化为数学问题,列出二(三)元一次方程组,最终求得符合实际的解.解一次方程组的基本思想是消元、转化:通过消元,把三元一次方程组转化为二元一次方程组,把二元一次方程组转化为一元一次方程.最常见的消元方法有代入法和加减法.一个方程组用什么方法来逐步消元,应根据它的特点灵活选定.通过列方程组来解实际问题,应注意检验和正确作答.检验不仅要检查求得的解是否满足所列方程组中的每一个方程,而且要检验所得的解答是否符合实际问题的要求.教学建议数感模型思想有效应用模型思想是学生体会和理解数学与实际问题的基本途径,能够提高学生学习数学的兴趣和应用意识建立数感有助于学生理解现实生活中数的意义,理解或表述具体情境中的数量关系培养运算能力有助于学生理解运算的算理,寻求合理简洁的运算途径解决问题数学抽象数学运算运算能力数学建模核 心素 养通过问题解决梳理知识体系通过思想方法沟通知识联系通过变式训练提高解题能力通过思路分析提升思维水平核心思想学生在课堂教学中有哪些出乎你意料的良好表现,好的解题方法,新的分析问题的思路,敏锐的观察发现,深刻的问题剖析,提出新的质疑,对问题独特的见解……在课堂教学中,对于随机发生的教学情况有什么好的应对办法,对于学生随机生成的教学问题有什么好的解答方式,对教学的方式有什么新的想法,有什么新的解题思路……本节课最遗憾的地方是什么,造成失误或遗憾的原因有哪些。是设计不合理,还是对学生接受程度估计不够,是教学内容组织上的问题,还是对教材理解把握上出现偏差的原因……本节课什么地方最成功,成功的原因是什么教育是一门寻找遗憾的艺术,我们需要不断地反思并优化我们的教学过程,在过程与结果中寻找一个结合点,以达到教育的更高境界。谢谢大家!
次元大文章知识结构重要性一元一次方程经历从具体问题中的数量相等关系列出方程的过程,体会方程是刻画现实世界数量关系的有效的数学模型了解“方程、一元一次方程、方程的解、解方程”等基本概念.理解等式的基本性质,掌握方程的简单变形会解一元一次方程,并经历和体会解方程中“转化”的过程和思想.了解一元一次方程解法的一般步骤,并能正确、灵活应用在学习和探索一元一次方程的解法和应用中,通过自主学习,提高学习能力,增强合作意识通过实践与探索,经历“问题情景——建立数学模型——解释、应用与拓展”的过程,体会数学模型思想,提高分析和解决实际问题的能力能根据具体问题中的数量关系列出一元一次方程并求解,并能根据问题的实际意义检验所得结果是否合理教学
目标6.3 实践与探索复习6.1 从实际问题到方程6.2 解一元一次方程体会设元之后在思维、列式上直接明了的优点尝试检验法,寻求答案,引导学生学会检验解的正确性有效利用课标例题,
感受以上学习内容等式的基本性质方程的变形规则??一元一次方程:
只含有一个未知数,且所含未知数的式子都是整式,未知数的次数为1,这样的方程叫做一元一次方程。判断下列那些是一元一次方程:
(1) (2)
(3) (4)
(5) (6)
(7) (8)去括号时注意去括号法则注意:1.分数线有括号的作用
2.等式的基本性质0102030405去分母时分数线有括号的作用;不要漏乘不含分母的项括号前面是负号,去括号时注意括号内各项要改变符号移项时要变号将字母前的系数相加减,与字母和字母的指数无关乘以未知数系数的
倒数(除以未知数的系数)方程的变形规则2去括号法则方程的变形规则1合并同类项法则方程的变形规则2依据注意列表用代数式表示相关量分析等量关系画图用代数式表示相关量分析等量关系体会不同设元方法,根据题意合理、灵活地设元提出问题解决问题变式一
甲、乙两站相距162km,一列慢车从甲站开出,时速为36km;一列快车从乙站开出,时速48km,按照下列各情况列出方程。 (1) 两车同时开出相向而行,________h后相遇; (2) 慢车先开出1h,相向而行,快车开出_______h后两车相遇; (3) 两列火车同时开出,相背而行,________h后相距280km; (4) 两列火车同时同向而行,快车在慢车后面,________小时后可以追上慢车; (5) 快车先开出1小时,同向而行,快车在慢车后面,快车开出________小时后可追上慢车。变式二
甲、乙两人在环形跑道上练习跑步,已知环形跑道一圈长400米,乙每秒跑6米,甲每秒跑8米.
(1) 如果甲、乙两人在跑道上相距8米处同时反向出发,那么经过多少秒两人首次相遇?
(2) 如果甲在乙前面8米处同时同向出发,那么经过多少秒两人首次相遇?变式三
如图,两人沿着边长为90m的正方形行走,按A→B→C→D→A…方向,甲从A以65m/min的速度,乙从B以72m/min的速度行走,当乙第一次追上甲时,在正方形的哪一条边上?在应用一元一次方程解实际问题时,要学会分析问题的本领.能根据题意,将实际问题转化为数学问题,特别是寻求主要的数量相等关系,列出方程.求得方程的解后,要注意检验所得结果是否符合实际问题的要求.对一元一次方程的认识,要联系生活实际,在解决实际问题过程中体会:方程是反映现实世界数量相等关系的一个有效的数学模型.解一元一次方程时,既要注意合理地进行方程的变形,也要注意根据方程的特点灵活运用方程的变形规则.010302一次方程组掌握代入消元法和加减消元法,能解二元一次方程组通过列出一次方程组解决有多个未知数的实际问题,理解一次方程组及其解的基本概念,进一步体会方程和方程组是刻画现实世界数量关系的有效模型01*0302能解简单的三元一次方程组通过探求一次方程组的解法,经历从二元一次方程组到一元一次方程转化的过程.体会“消元”和“化归”的数学思想方法0405会根据实际问题中的数量关系列出一次方程组并求解,能检验所得结果是否符合题意0203042课时057.2 二元一次方程组的解法*7.3 三元一次方程组及其解法7.4 实践与探索复习012课时2课时5课时7.1 二元一次方程组和它的解1课时将二元转化为一元,概括代入消元法的基本方法和步骤由简到难,进一步体会“化归”思想在实际问题中,经常会遇到有多个未知量的问题.和一元一次方程一样,二(三)元一次方程组也是反映现实世界数量之间相等关系的数学模型.要学会将实际问题转化为数学问题,列出二(三)元一次方程组,最终求得符合实际的解.解一次方程组的基本思想是消元、转化:通过消元,把三元一次方程组转化为二元一次方程组,把二元一次方程组转化为一元一次方程.最常见的消元方法有代入法和加减法.一个方程组用什么方法来逐步消元,应根据它的特点灵活选定.通过列方程组来解实际问题,应注意检验和正确作答.检验不仅要检查求得的解是否满足所列方程组中的每一个方程,而且要检验所得的解答是否符合实际问题的要求.教学建议数感模型思想有效应用模型思想是学生体会和理解数学与实际问题的基本途径,能够提高学生学习数学的兴趣和应用意识建立数感有助于学生理解现实生活中数的意义,理解或表述具体情境中的数量关系培养运算能力有助于学生理解运算的算理,寻求合理简洁的运算途径解决问题数学抽象数学运算运算能力数学建模核 心素 养通过问题解决梳理知识体系通过思想方法沟通知识联系通过变式训练提高解题能力通过思路分析提升思维水平核心思想学生在课堂教学中有哪些出乎你意料的良好表现,好的解题方法,新的分析问题的思路,敏锐的观察发现,深刻的问题剖析,提出新的质疑,对问题独特的见解……在课堂教学中,对于随机发生的教学情况有什么好的应对办法,对于学生随机生成的教学问题有什么好的解答方式,对教学的方式有什么新的想法,有什么新的解题思路……本节课最遗憾的地方是什么,造成失误或遗憾的原因有哪些。是设计不合理,还是对学生接受程度估计不够,是教学内容组织上的问题,还是对教材理解把握上出现偏差的原因……本节课什么地方最成功,成功的原因是什么教育是一门寻找遗憾的艺术,我们需要不断地反思并优化我们的教学过程,在过程与结果中寻找一个结合点,以达到教育的更高境界。谢谢大家!
