华师大版八下 第19章 矩形、菱形正方形 课件(39张PPT)
文档属性
| 名称 | 华师大版八下 第19章 矩形、菱形正方形 课件(39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-19 16:32:29 | ||
图片预览







文档简介
课件39张PPT。第19章 矩形菱形正方形19.1 矩形 4课时
19.2 菱形 4课时
19.3正方形 2课时
复习 2课时
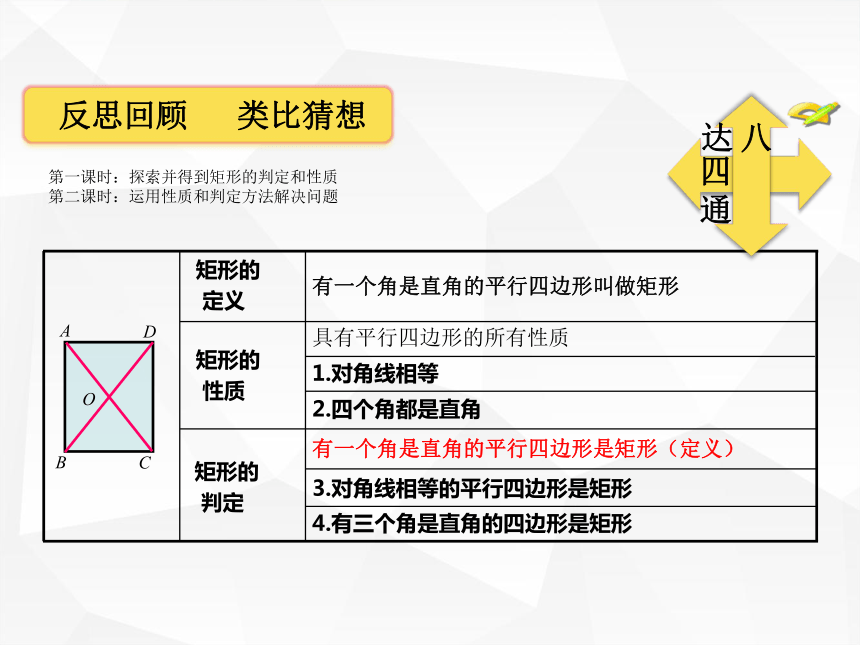
第19章课时安排 第一课时:探索并得到矩形的判定和性质
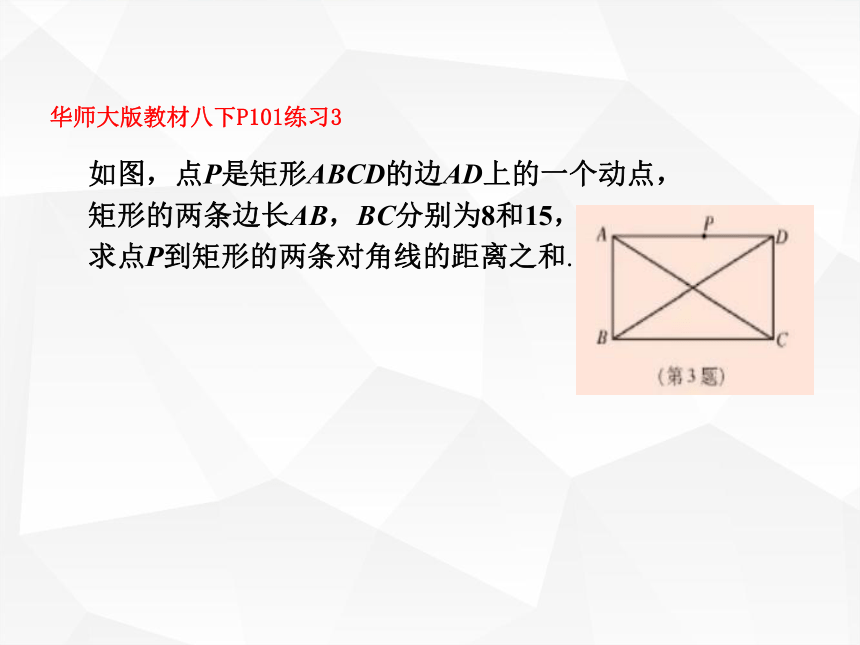
第二课时:运用性质和判定方法解决问题整合各版本教材,补充例题。北师大版教材九上P13例1,(对角线成角60°伴随等边三角形同时出现)华师大版教材八下P101练习3如图,点P是矩形ABCD的边AD上的一个动点,
矩形的两条边长AB,BC分别为8和15,
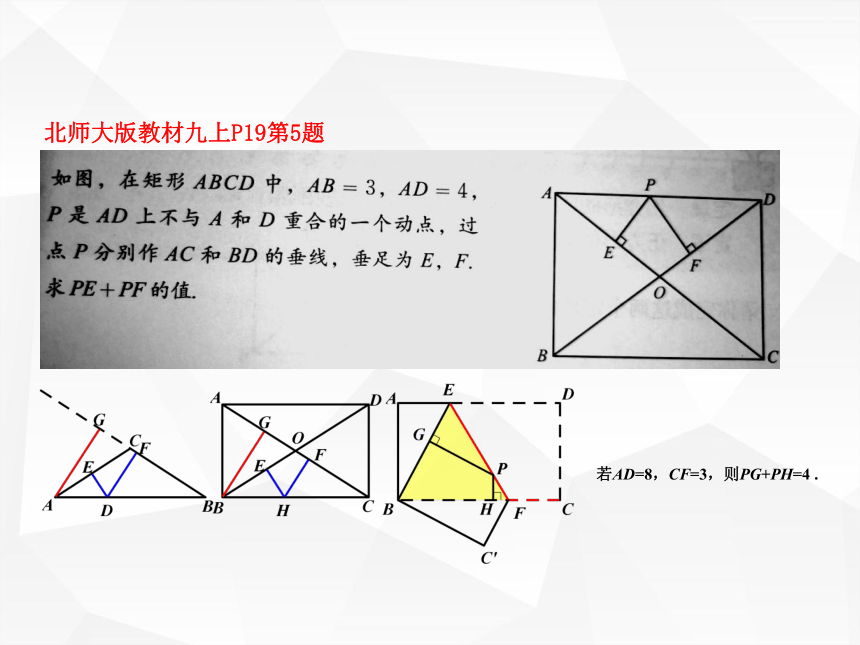
求点P到矩形的两条对角线的距离之和. 北师大版教材九上P19第5题若AD=8,CF=3,则PG+PH=4 . 北师大版教材九上P17例4
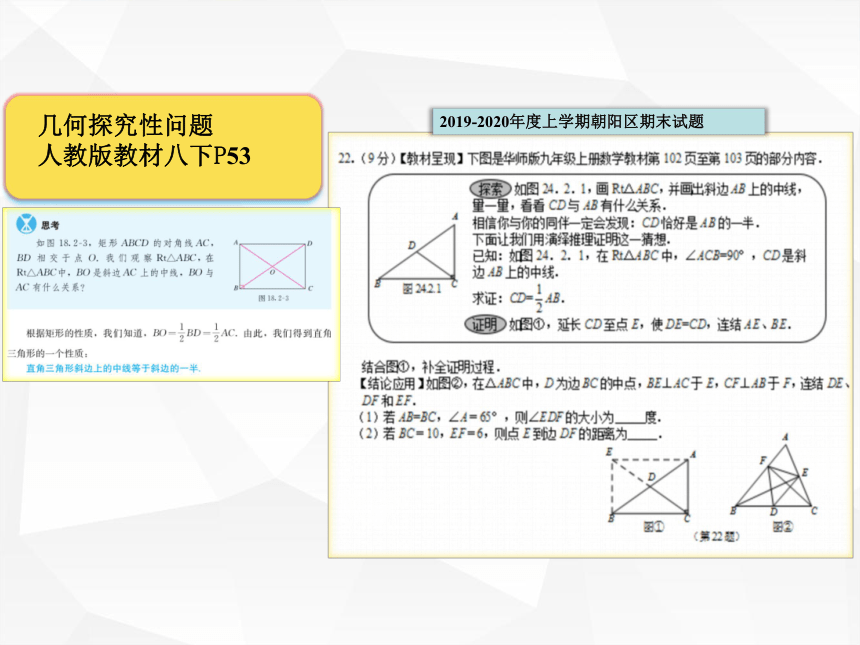
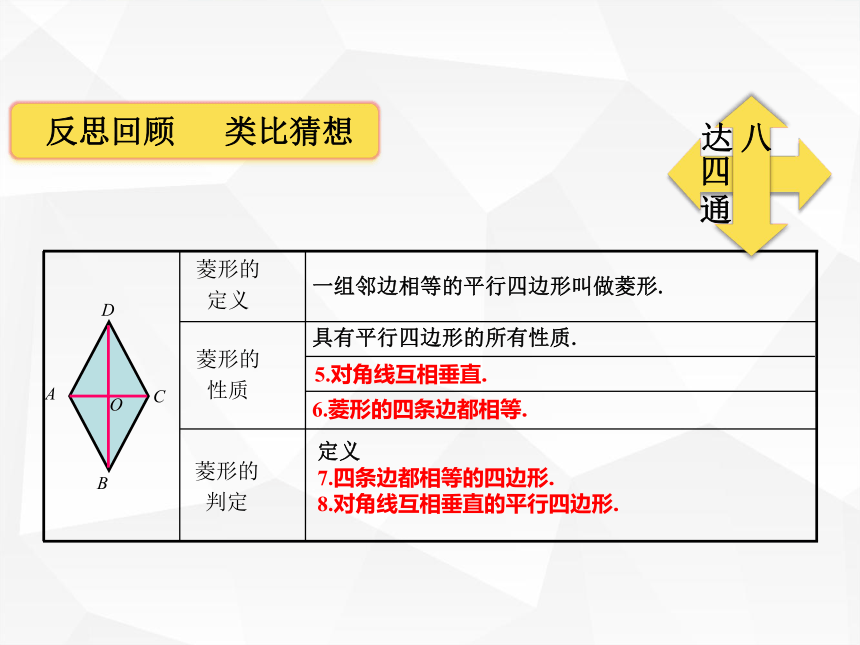
矩形判定定理:有三个角是直角的四边形是矩形.华师版教材八下P105例6 矩形判定定理:对角线相等的平行四边形是矩形. 补充问题:巩固矩形对角线相等的特性2019-2020年度上学期朝阳区期末试题 5.对角线互相垂直.定义
7.四条边都相等的四边形.
8.对角线互相垂直的平行四边形.菱形内角60°或120°时,伴随等边三角形同时出现.菱形对角线互相垂直平分,伴随直角三角形同时出现.华师版教材P112——例2
在菱形ABCD中,∠B=60°,AC为对角线.点 、F分别在边AB、DA或其延长线上,
连结CE、CF,且∠ECF=60°.
【感知】如图①,当点E、F分别在边AB、DA上时,易证:AF=BE .(不要求证明)
【探究】如图②,当点E、F分别在边AB、DA的延长线上时,CF与边AB交于点G.
求证:AF=BE .
【应用】如图②,若AB=12,AF=4,求线段GE的长.
如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AH⊥BC于点H,已知BO=4,S菱形ABCD=24,则AH= .面积求法如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
(A)1.(B)2.(C)3.(D)4.对称性,最短距离问题矩形菱形正方形【问题1】华师版八下P121习题19.3第2题
如图,在正方形ABCD中,CE⊥DF.求证:CE=DF.
正方形中的十字架(2018 山东省青岛市) 如图,已知正方形ABCD的边长为5,点E、F分别在AD、DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连结GH,则GH的长为 . 华师版八下P125B组第11题【问题2】如图,正方形ABCD的对角线相交于点O,点O又是另一个正方形A′B′C′O的一个顶点.如果两个正方形的边长相等,那么正方形A′B′C′O绕点O无论怎样旋转,两个正方形重叠的面积总等于一个正方形面积的四分之一.想一想,这是为什么?
(2014 四川省宜宾市) 如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是 .
【问题3】华师大版教材P126 C组第14题
(2011长春)
探究:如图①,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,连结AC、EF.在图中找一个与△FAE全等的三角形,并加以证明.
应用:以□ABCD的四条边为边,在其形外分别作正方形,如图②,连结EF、GH、IJ、KL.若□ABCD的面积为5,则图中阴影部分四个三角形的面积和为 .【几何探究】【问题4】华师版教材P75练习2 “对角线”一线牵【经典问题1】关于正方形的半角问题:
如图①,四边形ABCD是正方形,点E、F分别在BC、CD边上,且∠EAF=45°,
则EF=BE+DF.
如图②,四边形ABCD是正方形,点E、F分别在CB、DC的延长线上,且∠EAF=45°,
则EF,BE,DF又怎样的数量关系?
回味经典 历久弥新【经典问题2】如图,在正方形ABCD中,在边AB(或AB的延长线上)任一点E(不与A、B重合),∠DEF=90°,射线EF与∠ABC的外角平分线交于点F.
求证:DE=EF.
回味经典 历久弥新专题推荐
如图①,②为4×5的网格,每个小正方形的顶点称为格点.在图①中已画出线段AB,在图②中已画出线段CD,只用无刻度的直尺,在给定的网格中按要求画图,所画四边形的顶点均在格点上,不要求写出画法.
(1)在图①中以AB为边画一个四边形。且为中心对称图形.
(2)在图①中以AB为边画一个矩形(不是正方形).
(3)在图①中以AB为边画一个菱形(不是正方形).
(4)在图①中以AB为边画一个正方形.
(5)在图②中以CD为对角线画一个平行四边形.
(6)在图②中以CD为对角线画一个矩形.
(7)在图②中以CD为对角线画一个正方形.
(8)在图②中,用无刻度的直尺找到CD的中点.
网格作图第(8)问参考答案:让为人师者精心设计教学活动
在学生的思维空间里修路架桥
实现学生思维领域的四通八达谢谢大家!
19.2 菱形 4课时
19.3正方形 2课时
复习 2课时
第19章课时安排 第一课时:探索并得到矩形的判定和性质
第二课时:运用性质和判定方法解决问题整合各版本教材,补充例题。北师大版教材九上P13例1,(对角线成角60°伴随等边三角形同时出现)华师大版教材八下P101练习3如图,点P是矩形ABCD的边AD上的一个动点,
矩形的两条边长AB,BC分别为8和15,
求点P到矩形的两条对角线的距离之和. 北师大版教材九上P19第5题若AD=8,CF=3,则PG+PH=4 . 北师大版教材九上P17例4
矩形判定定理:有三个角是直角的四边形是矩形.华师版教材八下P105例6 矩形判定定理:对角线相等的平行四边形是矩形. 补充问题:巩固矩形对角线相等的特性2019-2020年度上学期朝阳区期末试题 5.对角线互相垂直.定义
7.四条边都相等的四边形.
8.对角线互相垂直的平行四边形.菱形内角60°或120°时,伴随等边三角形同时出现.菱形对角线互相垂直平分,伴随直角三角形同时出现.华师版教材P112——例2
在菱形ABCD中,∠B=60°,AC为对角线.点 、F分别在边AB、DA或其延长线上,
连结CE、CF,且∠ECF=60°.
【感知】如图①,当点E、F分别在边AB、DA上时,易证:AF=BE .(不要求证明)
【探究】如图②,当点E、F分别在边AB、DA的延长线上时,CF与边AB交于点G.
求证:AF=BE .
【应用】如图②,若AB=12,AF=4,求线段GE的长.
如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AH⊥BC于点H,已知BO=4,S菱形ABCD=24,则AH= .面积求法如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
(A)1.(B)2.(C)3.(D)4.对称性,最短距离问题矩形菱形正方形【问题1】华师版八下P121习题19.3第2题
如图,在正方形ABCD中,CE⊥DF.求证:CE=DF.
正方形中的十字架(2018 山东省青岛市) 如图,已知正方形ABCD的边长为5,点E、F分别在AD、DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连结GH,则GH的长为 . 华师版八下P125B组第11题【问题2】如图,正方形ABCD的对角线相交于点O,点O又是另一个正方形A′B′C′O的一个顶点.如果两个正方形的边长相等,那么正方形A′B′C′O绕点O无论怎样旋转,两个正方形重叠的面积总等于一个正方形面积的四分之一.想一想,这是为什么?
(2014 四川省宜宾市) 如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是 .
【问题3】华师大版教材P126 C组第14题
(2011长春)
探究:如图①,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,连结AC、EF.在图中找一个与△FAE全等的三角形,并加以证明.
应用:以□ABCD的四条边为边,在其形外分别作正方形,如图②,连结EF、GH、IJ、KL.若□ABCD的面积为5,则图中阴影部分四个三角形的面积和为 .【几何探究】【问题4】华师版教材P75练习2 “对角线”一线牵【经典问题1】关于正方形的半角问题:
如图①,四边形ABCD是正方形,点E、F分别在BC、CD边上,且∠EAF=45°,
则EF=BE+DF.
如图②,四边形ABCD是正方形,点E、F分别在CB、DC的延长线上,且∠EAF=45°,
则EF,BE,DF又怎样的数量关系?
回味经典 历久弥新【经典问题2】如图,在正方形ABCD中,在边AB(或AB的延长线上)任一点E(不与A、B重合),∠DEF=90°,射线EF与∠ABC的外角平分线交于点F.
求证:DE=EF.
回味经典 历久弥新专题推荐
如图①,②为4×5的网格,每个小正方形的顶点称为格点.在图①中已画出线段AB,在图②中已画出线段CD,只用无刻度的直尺,在给定的网格中按要求画图,所画四边形的顶点均在格点上,不要求写出画法.
(1)在图①中以AB为边画一个四边形。且为中心对称图形.
(2)在图①中以AB为边画一个矩形(不是正方形).
(3)在图①中以AB为边画一个菱形(不是正方形).
(4)在图①中以AB为边画一个正方形.
(5)在图②中以CD为对角线画一个平行四边形.
(6)在图②中以CD为对角线画一个矩形.
(7)在图②中以CD为对角线画一个正方形.
(8)在图②中,用无刻度的直尺找到CD的中点.
网格作图第(8)问参考答案:让为人师者精心设计教学活动
在学生的思维空间里修路架桥
实现学生思维领域的四通八达谢谢大家!
