华师大版数学八下 第18章 平行四边形 课件(56张PPT)
文档属性
| 名称 | 华师大版数学八下 第18章 平行四边形 课件(56张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-20 00:00:00 | ||
图片预览










文档简介
课件56张PPT。目 录四
通
八
达 《义务教育数学课程标准(2011年版)》明确提出
10个核心素养——
运算能力
推理能力
模型思想
应用意识
创新意识 数感
符号意识
空间观念
几何直观
数据分析观念
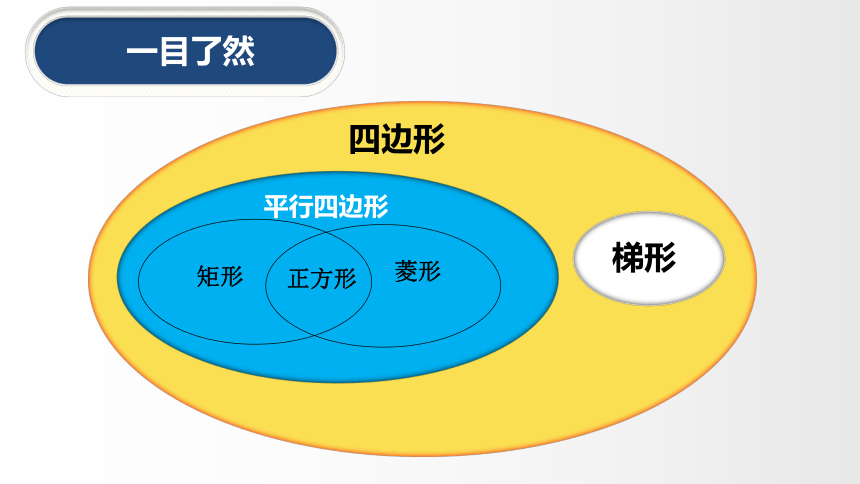
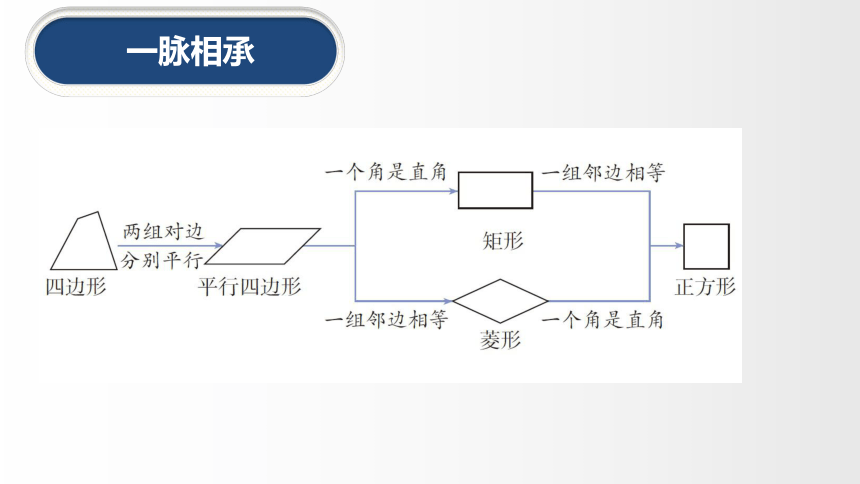
1.理解四个概念:理解平行四边形、矩形、菱形、正方形的概念,以及它们之间的关系;了解四边形的不稳定性.
2.(四通)探索并证明平行四边形的性质定理:平行四边形的对边相等、对角相等、对角线互相平分;
探索并证明平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
3.弄清三个距离.
了解两条平行线间距离的意义,能度量两条平行线之间的距离.
理解两点间距离的意义,能度量两点间的距离.
理解点到直线的距离的意义,能度量点到直线的距离.
4.(八达)四条性质定理+四条判定定理:探索并证明矩形、菱形的性质定理和判定定理.
(正方形的性质和判定是矩形、菱形的性质和判定的叠加)
探索并证明矩形、菱形、正方形的性质定理:(1)矩形的四个角都是直角,(2)对角线相等;(3)菱形的四条边相等,(4)对角线互相垂直;以及它们的判定定理:(5)三个角是直角的四边形是矩形,(6)对角线相等的平行四边形是矩形;(7)四条边相等的四边形是菱形,(8)对角线互相垂直的平行四边形是菱形。正方形具备矩形和菱形的一切性质。
四边形梯形平行四边形矩形正方形菱形第一学段已学过平行四边形的定义,本学段已学了平行线,三角形,全等三角形。这些都是学习第18章平行四边形的基础。通过平行四边形角、边的特殊化,研究19章矩形、菱形和正方形等特殊的平行四边形,认识概念之间的联系和区别;探索并证明平行四边形矩形、菱形和正方形的性质定理和判定定理,进一步明确命题及逆命题的关系,发展学生合情推理和演绎推理能力。教材在内容安排上,增大了学生自主探索的空间,按照“探索——猜想——证明”的顺序展开,体现了借助几何直观或逆向思维进行合情推理的过程,也体现了合情推理与演绎推理的有机结合.
教学流程:概念——性质——判定——应用.
推理顺序:几何直观——合情推理——演绎推理.
认知角度:分类讨论:边、角、对角线、对称性、面积周长.
判定方法:逆向思维——演绎推理
数学思想:转化与化归思想
一般到特殊
四边形转化为三角形
主题式教学顺应时代的潮流在新课标的要求下应运而生,与旧的教育教学模式不同,这种形式的教学更加注重学生能力的培养,对教学过程中的一些实质性问题进行阐述和说明。主题式教学包含了五大版块:现实生活化、数学活动、演绎归纳、问题焦点、反馈矫正。单元主题式教学
初中数学单元主题式教学
所谓单元教学,一般来说就是以一个单元作为数学教学的基本单位,从整体出发,统筹安排,以一个又一个问题串或分类出的问题的几个方面,带动整个单元的教学,把教学的各个环节有机灵活的地结合起来,形成一个不可分割的教学整体。
单元主题教学是根据课程实施水平目标,确立若干个教学主题,教师遵循学生学习的一般规律,以主题为线索,开发和重组相关教学内容,进行连续课时单元教学的教学方式。
开展单元主题教学体现学习领域水平目标达成的针对性,知识技能教学的连贯性和生本化,生活化等特性。将整个教学置于具体的生活情境中,有利于学生对知识技能的意义建构,重视学生技能的综合运用的实践体验,提高学生理解和运用知识和技能的能力和意识。
第18章课时安排 18.1 平行四边形的性质 4课时
18.2 平行四边形的判定 4课时
复习 2课时
单元主题式教学:18.1平行四边形的性质 观察这些图片,它们是否都有平行四边形的形象? 你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.第18章平行四边形第1课时一气呵成 我们用符号“△”与三个顶点字母表示三角形;对
于平行四边形,我们也有类似的表示方法吗? □ ABCD 边:对边,邻边;
角:对角,邻角;
对角线:平行四边形不相邻的两个顶点连成的线段.
【做一做】依据定义画平行四边形:
借助网格纸,尺规作图等
由定义得出:
平行四边形的两组对边分别平行.
【想一想】
它的边之间还有什么关系?
角之间有什么关系?
两条对角线有什么关系?
如图,在□ABCD中,对角线AC,BD 相交于点O.
猜想OA与OC,OB与OD有什么关系?并加以证明.
证明:OA=OC,OB=OD.理由如下:
∵ 四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC;
∴ ∠OAD=∠OCB,∠ADO=∠OBC;
∴ △AOD≌△COB;
∴ OA=OC,OB=OD.平行四边形是中心对称图形,对角线的交点是对称中心.【想一想】如何求出平行四边形的面积和周长呢?
周长为一组邻边和的2倍
面积是BC·AE?
AD·AE?
BC·CF?
AD·CF?
【新发现】平行线之间的距离处处相等.北师版教材五上P51深度挖掘数学本质
整合各种版本教材
设置问题要有梯度发展思维
提升素养
【问题1】 如图,在□ABCD中,∠A=40°,
求其余三个内角的度数. 【问题2】 如图,在□ABCD中,AB=8,其周长为24,
求其余三条边的长度.华师版教材P74例1,例2【问题3】如图,在□ABCD中,BD⊥AD,
垂足为D, AB=10,BD=8,求□ABCD周长和面积.
【问题4】如图,在□ABCD中,BD⊥AD,垂足为D,AC与BD交于点O,AB=10,BD=8.
求AC长;
求AB和CD间距离.
华师版教材例题5【问题5】如图,在□ABCD的对角线AC和BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC和BD的和是多少?
【问题6】(华师版教材例题6)如图,□ABCD的对角线AC和BD相交于点O,EF过点O且与边AB、CD分别相交于点E和点F.
(1)求证:OE=OF.
(2)若□ABCD的面积为20,则阴影面积为 .(补充问题)
(3)如图③,直线EF交BA延长线于点N,交DC延长线于点M,线段AN与CM的关系是 .
华师版教材例题7【问题7】华师版教材P79练习3【问题8】 CF+BE=AB
EF=2OF【问题9】(2019 四川省遂宁市).如图,□ABCD中,对角线AC、BD相交于点O,OE⊥BD交AD于点E,连结BE,若□ABCD的周长为28,则△ABE的周长为( )
(A)28 (B)24 ( C)21 ( D)14
深挖教材习题
变式成微专题 【问题1】
(2)若CD=8,AD=3,则AE= , BE= .
(3)如图,∠ADC的平分线交CB的延长线于点F.求证:DF=DC.
教材例题4
一条内角平分线 邻角平分线垂直【问题2】直角顶点的位置不同(1)若AB=8,AD=5,则EF= .
(2)若AB=10,AD=4,则EF= .
华师版教材P76练习3平行四边形的对角的平分线平行 【问题3】如图,在□ABCD中,∠ABC的平分线交CD于点F,∠ADC的平分线交AB于点E.
求证:DE∥BF.
四边形DEBF是平行四边形(定义)
?
对边中点 【问题4】如图,在□ABCD中,点E和 点F分别为AB和CD的中点.
求证:DE∥BF .
中点问题【问题5】如图,在□ABCD中,E是BC的中点,连结AE并延长交DC的延长线交于点F.
(1)求证:AB=CF;
(2)连结DE,若AD=2AB,求证:DE⊥AF.
整合各版本教材高线问题人教版P42例1【问题6】如图,□ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.
添加条件:DH⊥BC,BG⊥AD垂足分别为H,G.DH与BF交于点P,BG交DE于点Q.求证:四边形DQBP是平行四边形.
1.如图,将□ABCD中沿对角线BD翻折,点C落在点C'处,BF交AD于点E.BC=8,AE=2,则BE的长为 6 .
“角分平等腰成”轴对称变换求线段长
图形变化与平行四边形
轴对称变换求角度2. 如图,在□ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为36°.3.如图,△ABC沿BC方向平移到△DEF的位置,若AC=5cm,BC=4cm,CE=3cm,则阴影部分面积为 cm2.
平移变换求面积4.(2019安徽)如图,点E 在□ABCD内部,AF∥BE,DF∥CE.
(1)求证:△BCE≌△ADF;(ASA)
(2)设□ABCD的面积为 S ,四边形AEDF 的面积为 T ,
求 的值.2
图形变化综合5.(1)如图①,□ABCD的对角线AC和BD相交于点O,直线EF过点O,分别交AD、BC于点E和点F.
求证:AE=CF;
(2)如图②,将□ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于H,I.
求证:EI=FG.
单元主题式教学:平行四边形的判定教学策略一:利用平行四边形的性质定理,把性质定理的条件和结论互换,逆向思维.通过合情推理,提出猜想,演绎推理证明.
教学策略二:教学中,还可以通过条件的增减、结论的改变等方法,对学生进行训练,培养学生的创新意识和数学思维.
人教版教材P46
对角线互相平分的四边形是平行四边形人教版教材P45
删掉 在上题中,将“E,F分别是AB,CD的中点”改为
“E,F分别是AB,CD上的点,且AE=CF”,结论是否
仍然成立?请说明理由. 【问题1】如图,在□ABCD中,E,F分别是AB,CD的
中点.求证:四边形EBFD是平行四边形.人教版教材P47例4
华师版教材P47例1
【问题2】如图,在□ABCD 中,E,F分别是对角线AC 上
的两点,并且 AE=CF.求证:四边形BFDE是平行四边形.O 还有其他证明方法吗?
你更喜欢哪一种证法. 华师版教材P86例2
灵活运用 掌握新知O 在上题□ABCD中,若点E,F 分别在AC 两侧的延长线上,
如图,其他条件不变,结论还成立吗?请证明你的结论. 灵活运用 掌握新知“两组对角相等的四边形是平行四边形”在课程标准中已删除【几何探究1】 如图,△ABC中,D,E分别是边AB,AC 的中点,
连结DE. 像DE这样,连结三角形两边中点的线段叫做
三角形的中位线. 看一看,量一量,猜一猜:
DE与BC之间有什么位置关
系和数量关系? 【几何探究2】人教版教材八下P48(北师大版教材八下P150三角形的中位线)
我们在研究平行四边形时,经常采用把平行四边形
转化为三角形的问题,能否用平行四边形研究三角形呢? 探究:写出证明过程
应用:如图,在□ABCD中,点O是对角线AC、BD的交点,
点E是边CD的中点,点F在BC的延长线上,且CF=BC,
求证:四边形OCFE是平行四边形.
拓展:已知:如图,△ABC是锐角三角形.分别以AB,AC为边向外侧作等边三角形ABM和等边三角形ACN.
D、E、F分别是MB,BC,CN的中点,连结DE,FE.
求证:DE=DF.
通
八
达 《义务教育数学课程标准(2011年版)》明确提出
10个核心素养——
运算能力
推理能力
模型思想
应用意识
创新意识 数感
符号意识
空间观念
几何直观
数据分析观念
1.理解四个概念:理解平行四边形、矩形、菱形、正方形的概念,以及它们之间的关系;了解四边形的不稳定性.
2.(四通)探索并证明平行四边形的性质定理:平行四边形的对边相等、对角相等、对角线互相平分;
探索并证明平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
3.弄清三个距离.
了解两条平行线间距离的意义,能度量两条平行线之间的距离.
理解两点间距离的意义,能度量两点间的距离.
理解点到直线的距离的意义,能度量点到直线的距离.
4.(八达)四条性质定理+四条判定定理:探索并证明矩形、菱形的性质定理和判定定理.
(正方形的性质和判定是矩形、菱形的性质和判定的叠加)
探索并证明矩形、菱形、正方形的性质定理:(1)矩形的四个角都是直角,(2)对角线相等;(3)菱形的四条边相等,(4)对角线互相垂直;以及它们的判定定理:(5)三个角是直角的四边形是矩形,(6)对角线相等的平行四边形是矩形;(7)四条边相等的四边形是菱形,(8)对角线互相垂直的平行四边形是菱形。正方形具备矩形和菱形的一切性质。
四边形梯形平行四边形矩形正方形菱形第一学段已学过平行四边形的定义,本学段已学了平行线,三角形,全等三角形。这些都是学习第18章平行四边形的基础。通过平行四边形角、边的特殊化,研究19章矩形、菱形和正方形等特殊的平行四边形,认识概念之间的联系和区别;探索并证明平行四边形矩形、菱形和正方形的性质定理和判定定理,进一步明确命题及逆命题的关系,发展学生合情推理和演绎推理能力。教材在内容安排上,增大了学生自主探索的空间,按照“探索——猜想——证明”的顺序展开,体现了借助几何直观或逆向思维进行合情推理的过程,也体现了合情推理与演绎推理的有机结合.
教学流程:概念——性质——判定——应用.
推理顺序:几何直观——合情推理——演绎推理.
认知角度:分类讨论:边、角、对角线、对称性、面积周长.
判定方法:逆向思维——演绎推理
数学思想:转化与化归思想
一般到特殊
四边形转化为三角形
主题式教学顺应时代的潮流在新课标的要求下应运而生,与旧的教育教学模式不同,这种形式的教学更加注重学生能力的培养,对教学过程中的一些实质性问题进行阐述和说明。主题式教学包含了五大版块:现实生活化、数学活动、演绎归纳、问题焦点、反馈矫正。单元主题式教学
初中数学单元主题式教学
所谓单元教学,一般来说就是以一个单元作为数学教学的基本单位,从整体出发,统筹安排,以一个又一个问题串或分类出的问题的几个方面,带动整个单元的教学,把教学的各个环节有机灵活的地结合起来,形成一个不可分割的教学整体。
单元主题教学是根据课程实施水平目标,确立若干个教学主题,教师遵循学生学习的一般规律,以主题为线索,开发和重组相关教学内容,进行连续课时单元教学的教学方式。
开展单元主题教学体现学习领域水平目标达成的针对性,知识技能教学的连贯性和生本化,生活化等特性。将整个教学置于具体的生活情境中,有利于学生对知识技能的意义建构,重视学生技能的综合运用的实践体验,提高学生理解和运用知识和技能的能力和意识。
第18章课时安排 18.1 平行四边形的性质 4课时
18.2 平行四边形的判定 4课时
复习 2课时
单元主题式教学:18.1平行四边形的性质 观察这些图片,它们是否都有平行四边形的形象? 你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.第18章平行四边形第1课时一气呵成 我们用符号“△”与三个顶点字母表示三角形;对
于平行四边形,我们也有类似的表示方法吗? □ ABCD 边:对边,邻边;
角:对角,邻角;
对角线:平行四边形不相邻的两个顶点连成的线段.
【做一做】依据定义画平行四边形:
借助网格纸,尺规作图等
由定义得出:
平行四边形的两组对边分别平行.
【想一想】
它的边之间还有什么关系?
角之间有什么关系?
两条对角线有什么关系?
如图,在□ABCD中,对角线AC,BD 相交于点O.
猜想OA与OC,OB与OD有什么关系?并加以证明.
证明:OA=OC,OB=OD.理由如下:
∵ 四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC;
∴ ∠OAD=∠OCB,∠ADO=∠OBC;
∴ △AOD≌△COB;
∴ OA=OC,OB=OD.平行四边形是中心对称图形,对角线的交点是对称中心.【想一想】如何求出平行四边形的面积和周长呢?
周长为一组邻边和的2倍
面积是BC·AE?
AD·AE?
BC·CF?
AD·CF?
【新发现】平行线之间的距离处处相等.北师版教材五上P51深度挖掘数学本质
整合各种版本教材
设置问题要有梯度发展思维
提升素养
【问题1】 如图,在□ABCD中,∠A=40°,
求其余三个内角的度数. 【问题2】 如图,在□ABCD中,AB=8,其周长为24,
求其余三条边的长度.华师版教材P74例1,例2【问题3】如图,在□ABCD中,BD⊥AD,
垂足为D, AB=10,BD=8,求□ABCD周长和面积.
【问题4】如图,在□ABCD中,BD⊥AD,垂足为D,AC与BD交于点O,AB=10,BD=8.
求AC长;
求AB和CD间距离.
华师版教材例题5【问题5】如图,在□ABCD的对角线AC和BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC和BD的和是多少?
【问题6】(华师版教材例题6)如图,□ABCD的对角线AC和BD相交于点O,EF过点O且与边AB、CD分别相交于点E和点F.
(1)求证:OE=OF.
(2)若□ABCD的面积为20,则阴影面积为 .(补充问题)
(3)如图③,直线EF交BA延长线于点N,交DC延长线于点M,线段AN与CM的关系是 .
华师版教材例题7【问题7】华师版教材P79练习3【问题8】 CF+BE=AB
EF=2OF【问题9】(2019 四川省遂宁市).如图,□ABCD中,对角线AC、BD相交于点O,OE⊥BD交AD于点E,连结BE,若□ABCD的周长为28,则△ABE的周长为( )
(A)28 (B)24 ( C)21 ( D)14
深挖教材习题
变式成微专题 【问题1】
(2)若CD=8,AD=3,则AE= , BE= .
(3)如图,∠ADC的平分线交CB的延长线于点F.求证:DF=DC.
教材例题4
一条内角平分线 邻角平分线垂直【问题2】直角顶点的位置不同(1)若AB=8,AD=5,则EF= .
(2)若AB=10,AD=4,则EF= .
华师版教材P76练习3平行四边形的对角的平分线平行 【问题3】如图,在□ABCD中,∠ABC的平分线交CD于点F,∠ADC的平分线交AB于点E.
求证:DE∥BF.
四边形DEBF是平行四边形(定义)
?
对边中点 【问题4】如图,在□ABCD中,点E和 点F分别为AB和CD的中点.
求证:DE∥BF .
中点问题【问题5】如图,在□ABCD中,E是BC的中点,连结AE并延长交DC的延长线交于点F.
(1)求证:AB=CF;
(2)连结DE,若AD=2AB,求证:DE⊥AF.
整合各版本教材高线问题人教版P42例1【问题6】如图,□ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.
添加条件:DH⊥BC,BG⊥AD垂足分别为H,G.DH与BF交于点P,BG交DE于点Q.求证:四边形DQBP是平行四边形.
1.如图,将□ABCD中沿对角线BD翻折,点C落在点C'处,BF交AD于点E.BC=8,AE=2,则BE的长为 6 .
“角分平等腰成”轴对称变换求线段长
图形变化与平行四边形
轴对称变换求角度2. 如图,在□ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为36°.3.如图,△ABC沿BC方向平移到△DEF的位置,若AC=5cm,BC=4cm,CE=3cm,则阴影部分面积为 cm2.
平移变换求面积4.(2019安徽)如图,点E 在□ABCD内部,AF∥BE,DF∥CE.
(1)求证:△BCE≌△ADF;(ASA)
(2)设□ABCD的面积为 S ,四边形AEDF 的面积为 T ,
求 的值.2
图形变化综合5.(1)如图①,□ABCD的对角线AC和BD相交于点O,直线EF过点O,分别交AD、BC于点E和点F.
求证:AE=CF;
(2)如图②,将□ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于H,I.
求证:EI=FG.
单元主题式教学:平行四边形的判定教学策略一:利用平行四边形的性质定理,把性质定理的条件和结论互换,逆向思维.通过合情推理,提出猜想,演绎推理证明.
教学策略二:教学中,还可以通过条件的增减、结论的改变等方法,对学生进行训练,培养学生的创新意识和数学思维.
人教版教材P46
对角线互相平分的四边形是平行四边形人教版教材P45
删掉 在上题中,将“E,F分别是AB,CD的中点”改为
“E,F分别是AB,CD上的点,且AE=CF”,结论是否
仍然成立?请说明理由. 【问题1】如图,在□ABCD中,E,F分别是AB,CD的
中点.求证:四边形EBFD是平行四边形.人教版教材P47例4
华师版教材P47例1
【问题2】如图,在□ABCD 中,E,F分别是对角线AC 上
的两点,并且 AE=CF.求证:四边形BFDE是平行四边形.O 还有其他证明方法吗?
你更喜欢哪一种证法. 华师版教材P86例2
灵活运用 掌握新知O 在上题□ABCD中,若点E,F 分别在AC 两侧的延长线上,
如图,其他条件不变,结论还成立吗?请证明你的结论. 灵活运用 掌握新知“两组对角相等的四边形是平行四边形”在课程标准中已删除【几何探究1】 如图,△ABC中,D,E分别是边AB,AC 的中点,
连结DE. 像DE这样,连结三角形两边中点的线段叫做
三角形的中位线. 看一看,量一量,猜一猜:
DE与BC之间有什么位置关
系和数量关系? 【几何探究2】人教版教材八下P48(北师大版教材八下P150三角形的中位线)
我们在研究平行四边形时,经常采用把平行四边形
转化为三角形的问题,能否用平行四边形研究三角形呢? 探究:写出证明过程
应用:如图,在□ABCD中,点O是对角线AC、BD的交点,
点E是边CD的中点,点F在BC的延长线上,且CF=BC,
求证:四边形OCFE是平行四边形.
拓展:已知:如图,△ABC是锐角三角形.分别以AB,AC为边向外侧作等边三角形ABM和等边三角形ACN.
D、E、F分别是MB,BC,CN的中点,连结DE,FE.
求证:DE=DF.
