华师大版八下 第17章 函数及其图象 说课课件(55张PPT)
文档属性
| 名称 | 华师大版八下 第17章 函数及其图象 说课课件(55张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 14.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-19 00:00:00 | ||
图片预览






文档简介
课件55张PPT。第17章 函数及其图象目 录《含英咀华话函数》“含英咀华”出自 唐·韩愈《进学解》:
“沉浸浓郁,含英咀华” 比喻读书吸取其精华.在此指吸取课标和教材的精华.
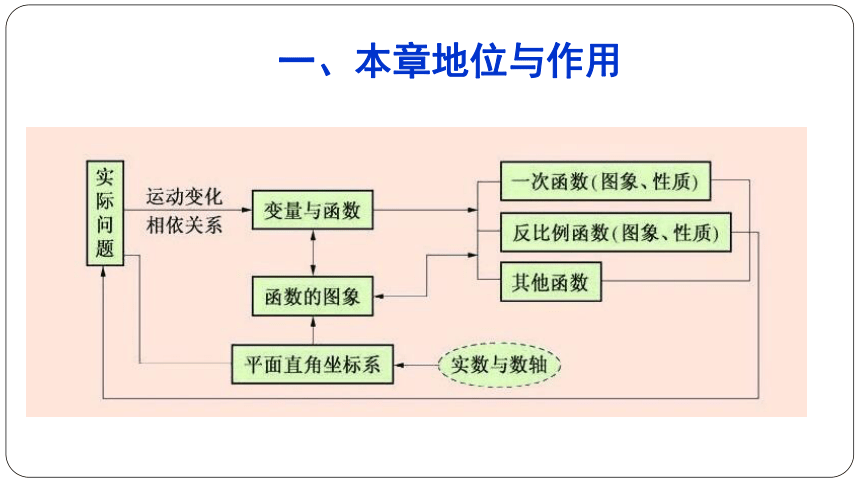
一、本章地位与作用一、本章地位与作用函数
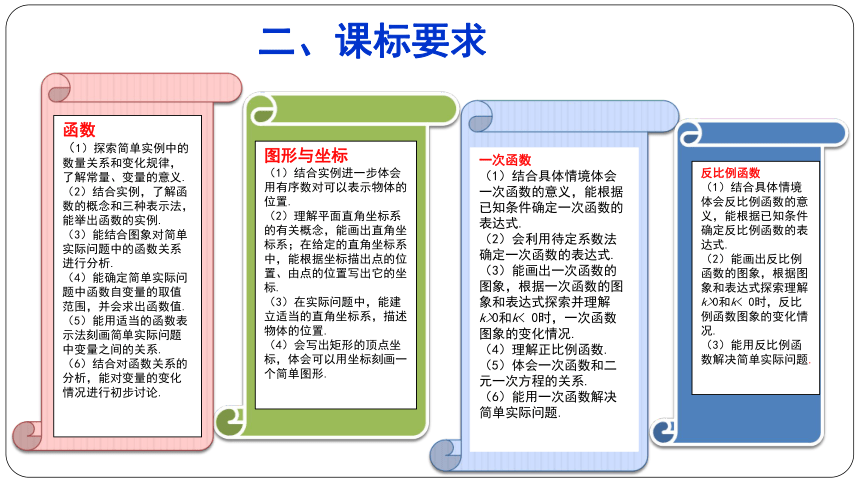
(1)探索简单实例中的数量关系和变化规律,了解常量、变量的意义.
(2)结合实例,了解函数的概念和三种表示法,能举出函数的实例.
(3)能结合图象对简单实际问题中的函数关系进行分析.
(4)能确定简单实际问题中函数自变量的取值范围,并会求出函数值.
(5)能用适当的函数表示法刻画简单实际问题中变量之间的关系.
(6)结合对函数关系的分析,能对变量的变化情况进行初步讨论.
一次函数
(1)结合具体情境体会一次函数的意义,能根据已知条件确定一次函数的表达式.
(2)会利用待定系数法确定一次函数的表达式.
(3)能画出一次函数的图象,根据一次函数的图象和表达式探索并理解 k>0和k< 0时,一次函数图象的变化情况.
(4)理解正比例函数.
(5)体会一次函数和二元一次方程的关系.
(6)能用一次函数解决简单实际问题.
二、课标要求图形与坐标
(1)结合实例进一步体会用有序数对可以表示物体的位置.
(2)理解平面直角坐标系的有关概念,能画出直角坐标系;在给定的直角坐标系中,能根据坐标描出点的位置、由点的位置写出它的坐标.
(3)在实际问题中,能建立适当的直角坐标系,描述物体的位置.
(4)会写出矩形的顶点坐标,体会可以用坐标刻画一个简单图形.
反比例函数
(1)结合具体情境体会反比例函数的意义,能根据已知条件确定反比例函数的表达式.
(2)能画出反比例函数的图象,根据图
象和表达式探索理解 k>0和k< 0时,反比例函数图象的变化情况.
(3)能用反比例函数解决简单实际问题.
三、教学目标1.探索简单实例中的数量关系和变化规律,了解常量、变量的意义.
2 .结合实例,进一步体会用有序实数对可以表示物体的位置.进而理解平面直角坐标系的有关概念.能画出平面直角坐标系,并根据坐标描出点的位置.以及由点的位置写出它的坐标.能写出一个已知点关于坐标轴对称的点的坐标.能在实际问题中,建立适当的平面直角坐标系,描述物体的位置.
3 .结合实例,了解函数的概念和三种表示方法.能举出函数的实例,并能用适当的函数表示法刻画简单实际问题中变量之间的关系.能确定简单实际问题中函数自变量的取值范围,并会根据自变量的值,求出对应的函数值.
4.了解函数图象的意义,会用描点法画出简单函数的图象.能结合函数图像对简单实际问题中的函数关系进行分析,并对变量的变化情况进行初步讨论.
5 .结合具体情景体会一次函数和反比例函数的意义,能根据已知条件确定一次函数和反比例函数的表达式.能理解并应用待定系数法.
6 .能画出一次函数和反比例函数的图象.能分别根据函数的图像和表达式y=kx+b(k ≠ 0)探索并理解k>0和k<0时,图象的变化情况,由此理解和掌握相应的函数性质.
7 .体会一次函数与二元一次方程的关系. 8.能用一次函数和反比例函数解决简单的实际问题,让学生经历和体会数学学习中问题情境—建立模型—解释应用—回顾拓展的过程,强化数学的应用意识,提高分析问题和解决问题的能力.
9.在探究性学习过程中,体会其中体现的方程、函数思想,以及类比、化归、数形结合、待定系数法等诸多数学思想方法.
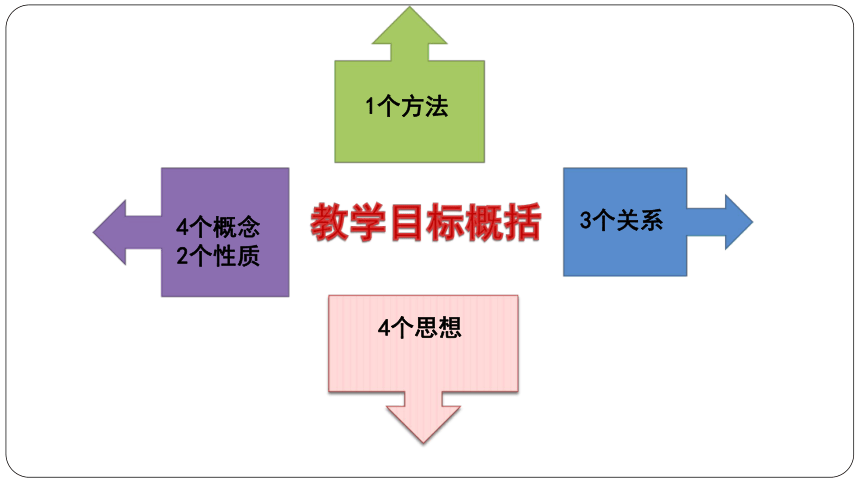
教学目标概括4个概念
2个性质1个方法3个关系4个思想
四、课时安排 17.1 变量与函数 2课时
17.2 函数的图象 2课时
17.3一次函数 5课时
17.4反比例函数 2课时
17.5实践与探索 3课时
第17章复习 2课时
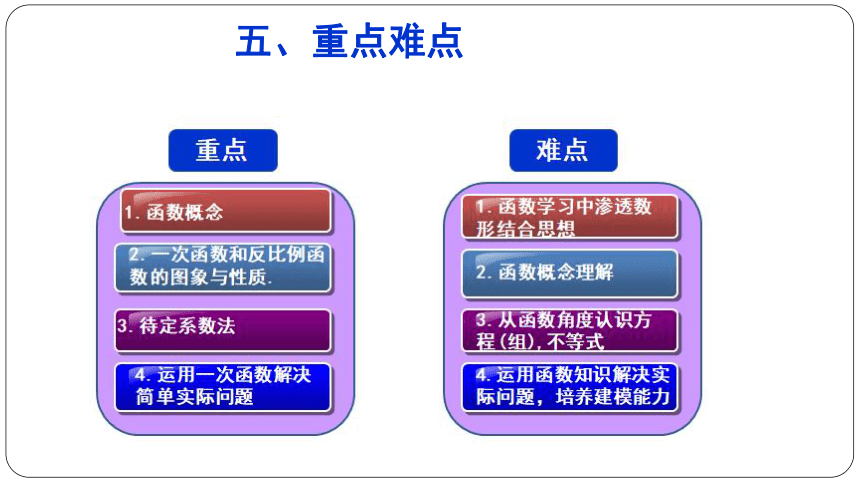
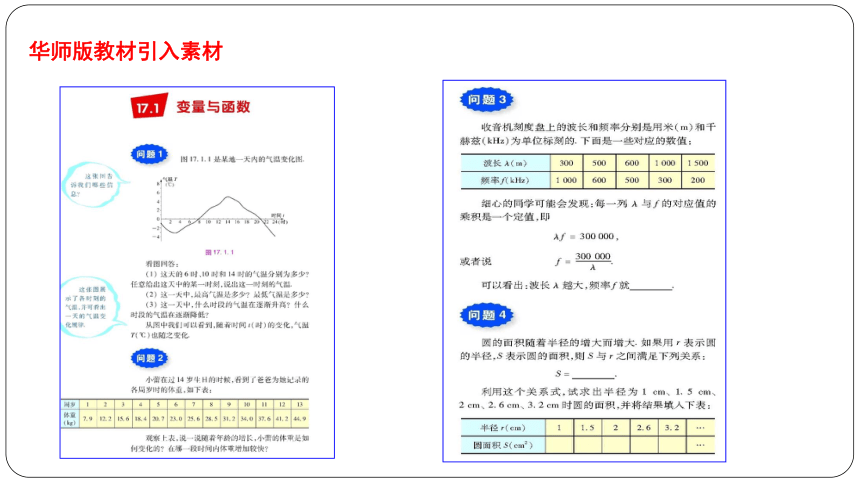
五、重点难点(一)细品教材,深化概念教学.从本质上认识函数概念 ,帮助学生弄清楚什么是函数六、重难点突破华师版教材引入素材其他版本教材函数概念引入素材概念辨析概念巩固1.学生举例子
2.看图说故事(课程标准123页例77)
设计两个不同的问题情境,使情境中出现的一对变量满足图示的函数关系。结合图象,讲出这对变量变化过程中的实际意义适当融入关于函数概念的数学史料1.李善兰
函数的英文是?fun_ction
我国清代著名数学家李善兰在翻译《代数学》这一书时,翻译成中文“函数”,一直沿用至今.“凡式中含天,为天之函数.”中国的古代人还用“天、地、人、物”4个字来表示4个不同的未知数或变量,显然,在李善兰的这个定义中的含义就是“凡是公式中含有变量x,则该式子叫做x的函数.”2.函数概念的发展史(二)由学生熟悉的几何图形入手,加深对函数概念、性质的认识,进一步体会数形结合思想1.初步感知几何图形运动变化中的函数关系教材69页第7题教材32页例题2在矩形ABCD中,AB=3,BC=4,动点P从点A开始按A→B→C→D的方向运动到点D.
设动点P所经过的路程为x,△APD的面积为y. (当点P与点A或D重合时,y=0)
扩展问题(1)写出y与x之间的函数关系式.
(2)画出此函数的图象.
(3)当x在什么范围内变化时,y随x的增大而增大?
(4)若7≤x≤8,则y的最大值为______________. 在正方形形ABCD中,AB=4,动点P从点A开始沿着A→B→C→D的方向以1/s的速度运动到点D. 所经过的路程为x,在这个运动变化过程中,设△APD的面积为s. (当点P与点A或D重合时,s=0),设动点P的运动时间为t(s),则s与t的变化关系用图象表示,正确的是( )
练习题配备教材70页第15题2.由一次函数与两坐标轴围成的三角形出发,进一步体会数形结合思想如图,直线y=kx+6与x轴、y轴分别相交于点E、F,点E的坐标为(﹣8,0),点A的坐标为(﹣6,0),点P是直线EF上的一个动点.
(1)求k的值;
(2)点P在第二象限内的直线EF上的运动过程中,写出△OPA的面积S与x的函整表达式,并写出自变量x的取值范围;
(3)探究,当点P在直线EF上运动到时,△OPA的面积可能是15吗,若能,请求出点P的坐标;若不能,说明理由.扩展问题一:面积存在性问题练习题配备如图,直线y=﹣2x+b与x轴,y轴分别相交于A、B两点,点B的坐标为(0,4),点C的坐标为(﹣4,0). (1)求直线AB的解析式. (2)求点A的坐标和AC的长. (3)若动点P(x,y)在直线AB上,则△PAC中AC边上的高为 . (用含x的式子表示) (4)若△PAC的面积为6,试确定点P的坐标. 扩展问题二:以一次函数为背景的动点问题如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的 时,求出这时点M的坐标.练习题配备扩展问题三:一次函数中的“一线三直角模型”练习题配备直线AB 与x轴负半轴、y轴正半轴分别交于A、B两点.
分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,
(1)△EPB的面积是否为定值?
(2)若为定值,请求出具体的值;若不确定,请说明理由. (三)用新老概念间的渗透突破一次函数与方程(组)和一元一次不等式的关系改编一:当点P到x轴的距离大于2个单位时,求m的取值范围.(3)若点P(m,n)在这条直线上改编二:当点P到x轴的距离大于2个单位且小于5个单位时,求m的取值范围.改编三:当点P到x轴和y轴的距离之和为5个单位时,求点P的坐标.(4)先画出该直线,然后在同一平面直角坐标系中再画出另一条直线y=2x+1改编四:求两条直线的交点坐标.改编五:当原直线在直线y=2x+1的上方时,求x的取值范围.教材68页第5题练习题配备在坐标系中作出函数y=2x+6的图象,利用图象解答下列问题:
(1)求方程2x+6=0的解;
(2)求不等式2x+6>0的解集;
(3)求不等式2x+6 <0的解集;
(4)求不等式2x+6>4的解集;
(3)若﹣2≤y≤2,求x的取值范围.教材42页第6题,64页第6题1.解读函数图像信息,培养应用意识扩展习题
人教版教材46页13题(四)在解决实际问题中,增强应用意识,培养学生的模型思想练习题配备2017年长春市数学中考试题第21题练习题配备2018年长春市数学中考试题第21题2.利用合理做决策和方案设计类问题,增强解决问题的能力扩展习题
北师版教材中96页第2题练习题配备随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB
(1)如图是yA与x之间函数关系的图象,请根据图象填空:m= ;n= .
(2)求出yB与x(x≥10)之间的函数关系式 .
(3)如果每月上网时间60小时,选择哪种方式上网学习合算,为什么?练习题配备 方案设计问题某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),
求W关于x的函数关系式,并求出x的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种
方案设计出来.3. 列出比较接近的函数表达式解决实际问题教材62页问题23扩展习题 课标106页例57扩展习题 北师版教材101页16题如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
(1)根据表中数据的规律,补全以下表格,并求出y关于x的函数表达式;(2)根据小明的身高和习惯,挎带的长度为120cm时,背起来
正合适,请求出此时单层部分的长度.
练习题配备从现实生活或具体情境中抽象数学问题——起点
用数学符号建立函数关系式
——关键步骤
利用函数的性质等相关知识去求出结果,并用此结果去解释、讨论它在现实问题中的意义. 归纳七、教学建议 (一)类比一次函数研究反比例函数
一次函数→反比例函数
研究内容:概念、图象、性质、应用
概念:体现概念教学的一般过程
图象:描点法、图象特征
性质:从k>0到k<0,从具体的函数到一般函数
应用:建立函数模型解决问题(二)夯实基础,加强函数学习方法引导,为后续学习做好铺垫通过对一次函数、反比例函数的学习.我们积累了一定的经验.下面我们借鉴
以往研究函数的经验,探索函数 图象和性质 探索性质
(1)填写下表,画出函数的图象:(2)观察图象,写出数两条不同类型的性质
解决问题
已知一个矩形的面积是4.设矩形的一边长为x.
它的周长为y.求y与x的函数关系式.函数探究活动:探究性质,完善基本技能,领悟基本思想,丰富基本活动经验请你用学习“一次函数”时积累的经验和方法研究函数y=|x|的图象和性质,并解决问题.
(1)完成下列步骤,画出函数y=|x|的图象;
①列表、填空; ②描点:③连线
(2)观察图象,当x 时,y随x的增大而增大;
(3)观察图象,写出该函数的两条性质
(4)结合图象,当x 时,函数值y=2
(5)结合图象,不等式|x|<x+2的解集为 .
练习题配备(三)适当的融入数学史料,加强数学文化渗透1.李善兰、函数概念的发展史(前面已经介绍)
2.中国古代的漏刻
3.笛卡尔:教材42页阅读材料
勒内·笛卡尔(Rene?Descartes,1596-1650),法国哲学家、数学家、物理学家。他对现代数学的发展做出了重要的贡献,因将几何坐标体系公式化而被认为是解析几何之父。他还是西方现代哲学思想的奠基人之一.4.利用函数测算岩石的年龄
5.反比例函数图象与三等分角
帕普斯:(Pappus)古希腊数学家,也译巴普士.生前有大量著作,但只有《数学汇编》保存下来.(四)借助微专题, 活化知识的运用,增加基本经验的积累微专题微专题1 一次函数最值问题
灵活运用一次函数的性质研究一次函数的最值,为后续二次函数的学习做好铺垫核心知识:一次函数的性质教材母题:50页第1题和53页第7题1.一次函数y=kx+b(k,b是常数,且k≠0)的图象如图所示.
(1)求k,b的值;
(2)当﹣1<x<5时,求y的变化范围,此时函数能取到最大值或者最小值吗?
(3)当﹣1<x≤5时,求y的变化范围,函数能取到最大值还是最小值?
(4)当﹣1≤x≤5时,求y的变化范围,并指出当x为何值时,y有最大值?并指
出当x为何值时,y有最小值?
2.一次函数y=ax-a+1(a为常数,且a≠0).当-1≤x≤2时,函数有最大值2,
请求出a的值. 搜集整理改编某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
思想方法归纳扩展升华微专题2 一次函数与行程问题
培养学生模型思想,从函数图象获取信息能力,培养学生运用数学知识解决问题能力(2019.长春.21)已知A,B两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止.甲、乙两车相距的路程y(千米)与甲车行驶的时间x(时)之间的函数关系式如图所示.
(1)乙车的速度为________千米/时,a=________,b=________.
(2)求甲、乙两车相遇后y与x之间的函数关系式.
(3)当甲车到距B地70千米处时,求甲、乙之间的路程.微专题3 新定义问题
借助新定义题型,培养学生的阅读理解能力、知识迁移能力和创新能力一次函数与平移
一次函数解析式
一次函数与轴对称
一次函数与等腰三角形
一次函数与将军饮马模型结合
一次函数解决利润问题
一次函数开放型问题
一次函数与全等三角形
一次函数面积专题
一次函数为载体的找规律问题等本学期还可以开发一次函数与四边形的微专题
微专题开发感谢您的倾听!
请提宝贵意见!
“沉浸浓郁,含英咀华” 比喻读书吸取其精华.在此指吸取课标和教材的精华.
一、本章地位与作用一、本章地位与作用函数
(1)探索简单实例中的数量关系和变化规律,了解常量、变量的意义.
(2)结合实例,了解函数的概念和三种表示法,能举出函数的实例.
(3)能结合图象对简单实际问题中的函数关系进行分析.
(4)能确定简单实际问题中函数自变量的取值范围,并会求出函数值.
(5)能用适当的函数表示法刻画简单实际问题中变量之间的关系.
(6)结合对函数关系的分析,能对变量的变化情况进行初步讨论.
一次函数
(1)结合具体情境体会一次函数的意义,能根据已知条件确定一次函数的表达式.
(2)会利用待定系数法确定一次函数的表达式.
(3)能画出一次函数的图象,根据一次函数的图象和表达式探索并理解 k>0和k< 0时,一次函数图象的变化情况.
(4)理解正比例函数.
(5)体会一次函数和二元一次方程的关系.
(6)能用一次函数解决简单实际问题.
二、课标要求图形与坐标
(1)结合实例进一步体会用有序数对可以表示物体的位置.
(2)理解平面直角坐标系的有关概念,能画出直角坐标系;在给定的直角坐标系中,能根据坐标描出点的位置、由点的位置写出它的坐标.
(3)在实际问题中,能建立适当的直角坐标系,描述物体的位置.
(4)会写出矩形的顶点坐标,体会可以用坐标刻画一个简单图形.
反比例函数
(1)结合具体情境体会反比例函数的意义,能根据已知条件确定反比例函数的表达式.
(2)能画出反比例函数的图象,根据图
象和表达式探索理解 k>0和k< 0时,反比例函数图象的变化情况.
(3)能用反比例函数解决简单实际问题.
三、教学目标1.探索简单实例中的数量关系和变化规律,了解常量、变量的意义.
2 .结合实例,进一步体会用有序实数对可以表示物体的位置.进而理解平面直角坐标系的有关概念.能画出平面直角坐标系,并根据坐标描出点的位置.以及由点的位置写出它的坐标.能写出一个已知点关于坐标轴对称的点的坐标.能在实际问题中,建立适当的平面直角坐标系,描述物体的位置.
3 .结合实例,了解函数的概念和三种表示方法.能举出函数的实例,并能用适当的函数表示法刻画简单实际问题中变量之间的关系.能确定简单实际问题中函数自变量的取值范围,并会根据自变量的值,求出对应的函数值.
4.了解函数图象的意义,会用描点法画出简单函数的图象.能结合函数图像对简单实际问题中的函数关系进行分析,并对变量的变化情况进行初步讨论.
5 .结合具体情景体会一次函数和反比例函数的意义,能根据已知条件确定一次函数和反比例函数的表达式.能理解并应用待定系数法.
6 .能画出一次函数和反比例函数的图象.能分别根据函数的图像和表达式y=kx+b(k ≠ 0)探索并理解k>0和k<0时,图象的变化情况,由此理解和掌握相应的函数性质.
7 .体会一次函数与二元一次方程的关系. 8.能用一次函数和反比例函数解决简单的实际问题,让学生经历和体会数学学习中问题情境—建立模型—解释应用—回顾拓展的过程,强化数学的应用意识,提高分析问题和解决问题的能力.
9.在探究性学习过程中,体会其中体现的方程、函数思想,以及类比、化归、数形结合、待定系数法等诸多数学思想方法.
教学目标概括4个概念
2个性质1个方法3个关系4个思想
四、课时安排 17.1 变量与函数 2课时
17.2 函数的图象 2课时
17.3一次函数 5课时
17.4反比例函数 2课时
17.5实践与探索 3课时
第17章复习 2课时
五、重点难点(一)细品教材,深化概念教学.从本质上认识函数概念 ,帮助学生弄清楚什么是函数六、重难点突破华师版教材引入素材其他版本教材函数概念引入素材概念辨析概念巩固1.学生举例子
2.看图说故事(课程标准123页例77)
设计两个不同的问题情境,使情境中出现的一对变量满足图示的函数关系。结合图象,讲出这对变量变化过程中的实际意义适当融入关于函数概念的数学史料1.李善兰
函数的英文是?fun_ction
我国清代著名数学家李善兰在翻译《代数学》这一书时,翻译成中文“函数”,一直沿用至今.“凡式中含天,为天之函数.”中国的古代人还用“天、地、人、物”4个字来表示4个不同的未知数或变量,显然,在李善兰的这个定义中的含义就是“凡是公式中含有变量x,则该式子叫做x的函数.”2.函数概念的发展史(二)由学生熟悉的几何图形入手,加深对函数概念、性质的认识,进一步体会数形结合思想1.初步感知几何图形运动变化中的函数关系教材69页第7题教材32页例题2在矩形ABCD中,AB=3,BC=4,动点P从点A开始按A→B→C→D的方向运动到点D.
设动点P所经过的路程为x,△APD的面积为y. (当点P与点A或D重合时,y=0)
扩展问题(1)写出y与x之间的函数关系式.
(2)画出此函数的图象.
(3)当x在什么范围内变化时,y随x的增大而增大?
(4)若7≤x≤8,则y的最大值为______________. 在正方形形ABCD中,AB=4,动点P从点A开始沿着A→B→C→D的方向以1/s的速度运动到点D. 所经过的路程为x,在这个运动变化过程中,设△APD的面积为s. (当点P与点A或D重合时,s=0),设动点P的运动时间为t(s),则s与t的变化关系用图象表示,正确的是( )
练习题配备教材70页第15题2.由一次函数与两坐标轴围成的三角形出发,进一步体会数形结合思想如图,直线y=kx+6与x轴、y轴分别相交于点E、F,点E的坐标为(﹣8,0),点A的坐标为(﹣6,0),点P是直线EF上的一个动点.
(1)求k的值;
(2)点P在第二象限内的直线EF上的运动过程中,写出△OPA的面积S与x的函整表达式,并写出自变量x的取值范围;
(3)探究,当点P在直线EF上运动到时,△OPA的面积可能是15吗,若能,请求出点P的坐标;若不能,说明理由.扩展问题一:面积存在性问题练习题配备如图,直线y=﹣2x+b与x轴,y轴分别相交于A、B两点,点B的坐标为(0,4),点C的坐标为(﹣4,0). (1)求直线AB的解析式. (2)求点A的坐标和AC的长. (3)若动点P(x,y)在直线AB上,则△PAC中AC边上的高为 . (用含x的式子表示) (4)若△PAC的面积为6,试确定点P的坐标. 扩展问题二:以一次函数为背景的动点问题如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的 时,求出这时点M的坐标.练习题配备扩展问题三:一次函数中的“一线三直角模型”练习题配备直线AB 与x轴负半轴、y轴正半轴分别交于A、B两点.
分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,
(1)△EPB的面积是否为定值?
(2)若为定值,请求出具体的值;若不确定,请说明理由. (三)用新老概念间的渗透突破一次函数与方程(组)和一元一次不等式的关系改编一:当点P到x轴的距离大于2个单位时,求m的取值范围.(3)若点P(m,n)在这条直线上改编二:当点P到x轴的距离大于2个单位且小于5个单位时,求m的取值范围.改编三:当点P到x轴和y轴的距离之和为5个单位时,求点P的坐标.(4)先画出该直线,然后在同一平面直角坐标系中再画出另一条直线y=2x+1改编四:求两条直线的交点坐标.改编五:当原直线在直线y=2x+1的上方时,求x的取值范围.教材68页第5题练习题配备在坐标系中作出函数y=2x+6的图象,利用图象解答下列问题:
(1)求方程2x+6=0的解;
(2)求不等式2x+6>0的解集;
(3)求不等式2x+6 <0的解集;
(4)求不等式2x+6>4的解集;
(3)若﹣2≤y≤2,求x的取值范围.教材42页第6题,64页第6题1.解读函数图像信息,培养应用意识扩展习题
人教版教材46页13题(四)在解决实际问题中,增强应用意识,培养学生的模型思想练习题配备2017年长春市数学中考试题第21题练习题配备2018年长春市数学中考试题第21题2.利用合理做决策和方案设计类问题,增强解决问题的能力扩展习题
北师版教材中96页第2题练习题配备随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB
(1)如图是yA与x之间函数关系的图象,请根据图象填空:m= ;n= .
(2)求出yB与x(x≥10)之间的函数关系式 .
(3)如果每月上网时间60小时,选择哪种方式上网学习合算,为什么?练习题配备 方案设计问题某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),
求W关于x的函数关系式,并求出x的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种
方案设计出来.3. 列出比较接近的函数表达式解决实际问题教材62页问题23扩展习题 课标106页例57扩展习题 北师版教材101页16题如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
(1)根据表中数据的规律,补全以下表格,并求出y关于x的函数表达式;(2)根据小明的身高和习惯,挎带的长度为120cm时,背起来
正合适,请求出此时单层部分的长度.
练习题配备从现实生活或具体情境中抽象数学问题——起点
用数学符号建立函数关系式
——关键步骤
利用函数的性质等相关知识去求出结果,并用此结果去解释、讨论它在现实问题中的意义. 归纳七、教学建议 (一)类比一次函数研究反比例函数
一次函数→反比例函数
研究内容:概念、图象、性质、应用
概念:体现概念教学的一般过程
图象:描点法、图象特征
性质:从k>0到k<0,从具体的函数到一般函数
应用:建立函数模型解决问题(二)夯实基础,加强函数学习方法引导,为后续学习做好铺垫通过对一次函数、反比例函数的学习.我们积累了一定的经验.下面我们借鉴
以往研究函数的经验,探索函数 图象和性质 探索性质
(1)填写下表,画出函数的图象:(2)观察图象,写出数两条不同类型的性质
解决问题
已知一个矩形的面积是4.设矩形的一边长为x.
它的周长为y.求y与x的函数关系式.函数探究活动:探究性质,完善基本技能,领悟基本思想,丰富基本活动经验请你用学习“一次函数”时积累的经验和方法研究函数y=|x|的图象和性质,并解决问题.
(1)完成下列步骤,画出函数y=|x|的图象;
①列表、填空; ②描点:③连线
(2)观察图象,当x 时,y随x的增大而增大;
(3)观察图象,写出该函数的两条性质
(4)结合图象,当x 时,函数值y=2
(5)结合图象,不等式|x|<x+2的解集为 .
练习题配备(三)适当的融入数学史料,加强数学文化渗透1.李善兰、函数概念的发展史(前面已经介绍)
2.中国古代的漏刻
3.笛卡尔:教材42页阅读材料
勒内·笛卡尔(Rene?Descartes,1596-1650),法国哲学家、数学家、物理学家。他对现代数学的发展做出了重要的贡献,因将几何坐标体系公式化而被认为是解析几何之父。他还是西方现代哲学思想的奠基人之一.4.利用函数测算岩石的年龄
5.反比例函数图象与三等分角
帕普斯:(Pappus)古希腊数学家,也译巴普士.生前有大量著作,但只有《数学汇编》保存下来.(四)借助微专题, 活化知识的运用,增加基本经验的积累微专题微专题1 一次函数最值问题
灵活运用一次函数的性质研究一次函数的最值,为后续二次函数的学习做好铺垫核心知识:一次函数的性质教材母题:50页第1题和53页第7题1.一次函数y=kx+b(k,b是常数,且k≠0)的图象如图所示.
(1)求k,b的值;
(2)当﹣1<x<5时,求y的变化范围,此时函数能取到最大值或者最小值吗?
(3)当﹣1<x≤5时,求y的变化范围,函数能取到最大值还是最小值?
(4)当﹣1≤x≤5时,求y的变化范围,并指出当x为何值时,y有最大值?并指
出当x为何值时,y有最小值?
2.一次函数y=ax-a+1(a为常数,且a≠0).当-1≤x≤2时,函数有最大值2,
请求出a的值. 搜集整理改编某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
思想方法归纳扩展升华微专题2 一次函数与行程问题
培养学生模型思想,从函数图象获取信息能力,培养学生运用数学知识解决问题能力(2019.长春.21)已知A,B两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止.甲、乙两车相距的路程y(千米)与甲车行驶的时间x(时)之间的函数关系式如图所示.
(1)乙车的速度为________千米/时,a=________,b=________.
(2)求甲、乙两车相遇后y与x之间的函数关系式.
(3)当甲车到距B地70千米处时,求甲、乙之间的路程.微专题3 新定义问题
借助新定义题型,培养学生的阅读理解能力、知识迁移能力和创新能力一次函数与平移
一次函数解析式
一次函数与轴对称
一次函数与等腰三角形
一次函数与将军饮马模型结合
一次函数解决利润问题
一次函数开放型问题
一次函数与全等三角形
一次函数面积专题
一次函数为载体的找规律问题等本学期还可以开发一次函数与四边形的微专题
微专题开发感谢您的倾听!
请提宝贵意见!
