华师大版数学八下 第20章 数据的整理与初步处理 说课课件(56张PPT)
文档属性
| 名称 | 华师大版数学八下 第20章 数据的整理与初步处理 说课课件(56张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-20 15:56:37 | ||
图片预览






文档简介
(共54张PPT)
三数一方争天下
说教材 道本质
促成长 拓思维
华为创始人任正非在接受
央视《面对面》采访时表示,
人工智能就是统计学,
大数据就是统计.
统计是研究如何合理地收集、整理、分析数据的科学,它可以为人们制定决策提供依据.
第20章 数据的整理与初步处理
目录
二 课标要求
四 教学建议
一 教材地位作用
三 教材分析
、
、
、
、
目录
二 课标要求
四 教学建议
一 教材地位作用
三 教材分析
、
、
、
、
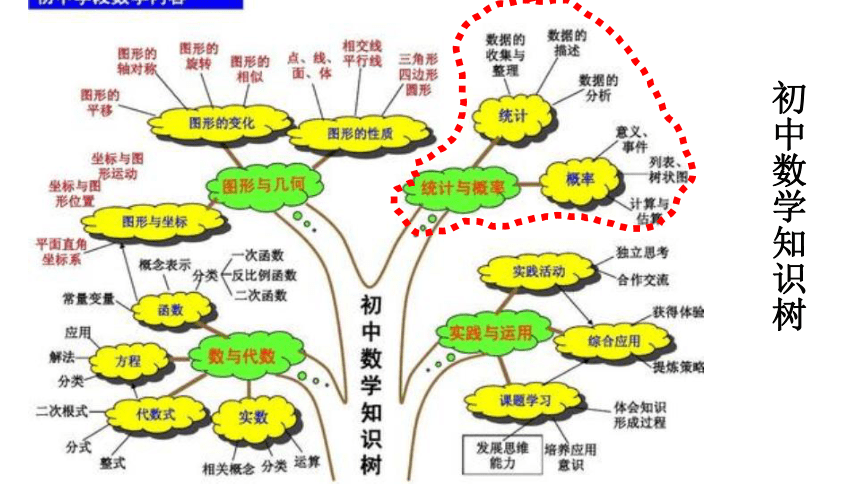
初中数学知识树
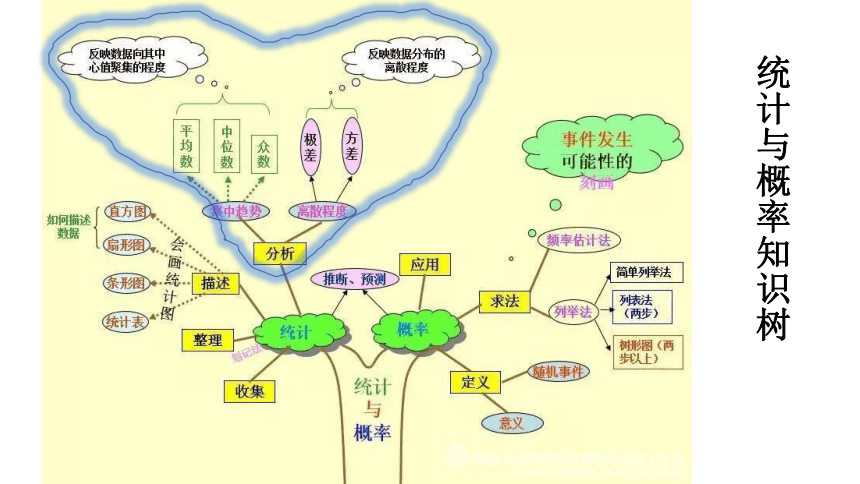
统计与概率知识树
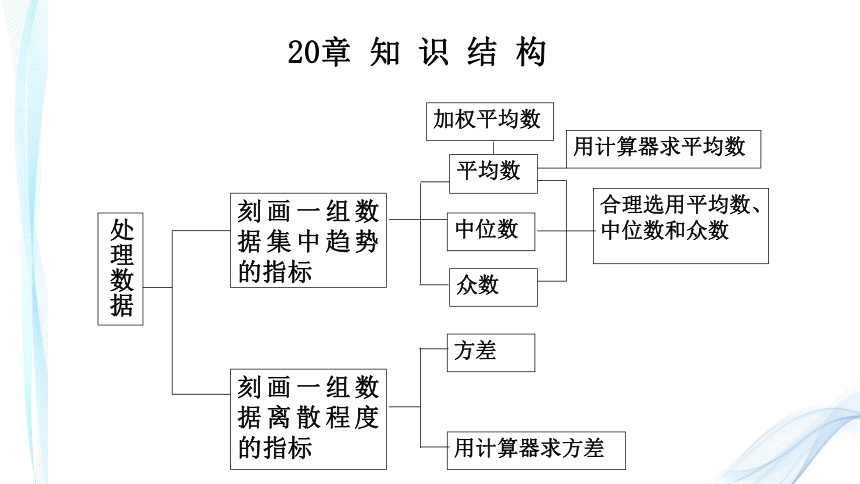
20章 知 识 结 构
处理数据
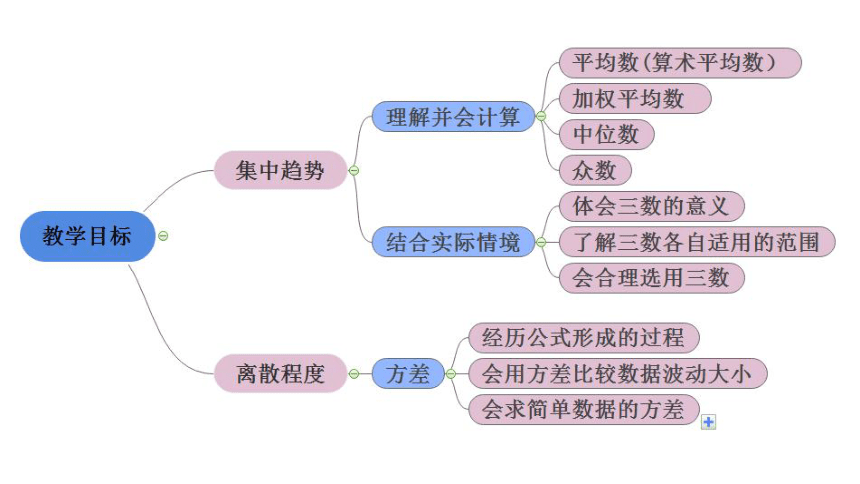
刻画一组数据集中趋势的指标
刻画一组数据离散程度的指标
加权平均数
平均数
中位数
众数
用计算器求平均数
方差
用计算器求方差
合理选用平均数、
中位数和众数
目录
二 课标要求
四 教学建议
一 教材地位作用
三 教材分析
、
、
、
、
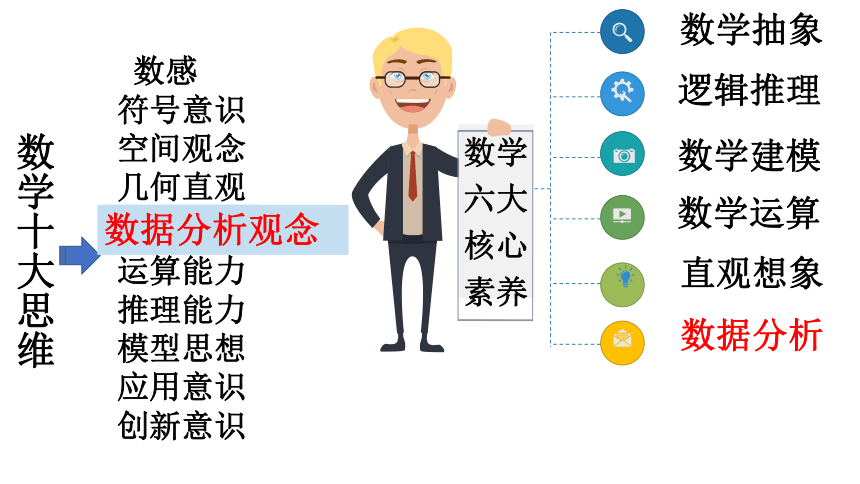
数学六大核心素养
数学抽象
逻辑推理
数学建模
数学运算
直观想象
数据分析
数感
符号意识
空间观念
几何直观
统计观念
运算能力
推理能力
模型思想
应用意识
创新意识
数学十大思维
统计观念
数据分析观念
目录
二 课标要求
四 教学建议
一 教材地位作用
三 教材分析
、
、
、
、
1. 课时分配
第1课时 20.1.1平均数的意义
第2课时 20.1.2用计算器求平均数
第3课时 20.1.3加权平均数
第4课时 20.2.1中位数和众数
第5课时 20.2.2平均数、中位数和众数的选用
第6课时 20. 3方差
第7课时 数据的离散程度
第20章复习
三、教材分析
2. 重难点分析
目录
二 课标要求
四 教学建议
一 教材地位作用
三 教材分析
、
、
、
、
难点突破一:“权”与“权重”
日常生活中,我们常用平均数表示一组数据的“一般水平”.
一般地,如果有 n 个数据 x1,x2,…,xn,我们用 表示这组数据的平均数,即
先求和,再平分.
求平均数的步骤:
7
6
5
4
3
2
1
A B C D
平均数
先总后均
移多补少
如图ABCD四个杯子中装了不同数量的小球,你能让四个杯子中的小球数目相同吗?
一般水平
超过平均数的总量等于不足平均数的总量
加权平均数
1.什么是权?
2.为什么要加权?
4.加权平均数与算术平均数有什么联系?
3.权和权重一样吗?
北京版七下教材:
“权”
北师版八上教材
人教版八下
华师版八下教参
例如:有5个数据2,2,2,8,8,
求平均数?
权
权重
权
形异质同
在实际问题中,一组数据里的各个数据的“重要程度” 未必相同.因而,在计算这组数据的平均数时,往往给每个数据一个“权”.
教学中应例举与学生生活实际,紧密相关的例子,可以让学生更好地体会加权平均数的意义.
为什么要加权?
教学建议:
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应聘者进行了听、说、读、写的英语水平测试,他们的各项成绩如表所示:
(1)如果公司想招一名综合能力较强的翻译,应该录用谁?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
合作探究
入情入境
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应聘者进行了听、说、读、写的英语水平测试,他们的各项成绩如表所示:
(2)如果公司想招一名笔译能力较强的翻译,用平均数来衡量他们的成绩合理吗?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
合作探究
听、说、读、写的成绩按照2:1:3:4的比确定.
探索合作
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应聘者进行了听、说、读、写的英语水平测试,他们的各项成绩如表所示:
(3)如果公司想招一名口语能力较强的翻译,怎么办?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
合作探究
听、说、读、写的成绩按照3:3:2:2的比确定.
方法反思
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应聘者进行了听、说、读、写的英语水平测试,他们的各项成绩如表所示:
(4)如果你是公司招聘的负责人,你将如何设置权重呢?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
合作探究
我能行,我做主!
叫做加权平均数,其中f1,f2,……,fk叫做权重.
加权平均数:如果n个数中,x1出现f1次,x2出现f2次,……,xk出现fk次,(这里f1+f2+……+fk=n),那么,根据平均数的定义,这n个数的平均数可以表示为
这样求得的平均数
加权平均数
算术平均数
权相等
当权相等时,设
难点突破二:
三数的合理选用
平均数反映了数据的“ 一般 水平”;
中位数反映了数据的“中等水平”;
众数反映了数据的“ 多数水平”.
选取多个统计量,综合分析
【教材144页问题2】八年级某班的教室里,三位同学正在为谁的数学成绩最好而争论,他们的五次数学成绩分别是:
小华: 62, 94, 95, 98, 98.
小明: 62, 62, 98, 99, 100.
小丽: 40, 62, 85, 99, 99.
他们都认为自己的成绩比另两位同学好,你看呢 完成下表:
平均数 中位数 众数
小华 89.4 95 98
小明 84.2 98 62
小丽 77 85 99
三数易错点归纳
① 忽略了加权平均数中“权”的存在
例:有8个数的平均数是10,还有12个数的平均数是12,则这20个数的平均数是 .
【错解】
(两个平均数所占权重是不同的,计算时要体现权重的存在)
【正解】
这20个数的平均数是11.2
② 求中位数时忽略了将数据排序
例:学校8名学生三月份参加义务劳动的时间(小时)分别为3,6,4,3,7,5,7,4,这组数据的中位数是 .
【错解】观察数据可得,中位数为第4、第5个位置的数据的平均数,即
【正解】先将数据进行排序:3,3,4,4,5,6,
7,7,因此中位数为
③忽略了数据的个数
例:广州某地连续10天的最高气温统计如下:
这组数据的中位数是 .
【错解】由图表可得5个温度:22、23、24、25、26,中间位置的数为24,所以中位数为24.
【正解】图表中22、23、24、25、26只是属于最高温度的类型,需要讨论的数据其实有10个:22、23、23、24、24、25、25、25、25、26,因此这组数据的中位数是
最高气温( C) 22 23 24 25 26
天数 1 2 2 4 1
④ 忽略了众数的个数
例:若数据8,7,8,x,5的平均数是7,则这组数据的众数是 .
本题很容易只写出一个众数,漏掉了另外一个.
【正解】由题意可得
,所以,x=7,故这组数据的众数为7、8.
难点突破三:方差的探索
在数学的天地里,重要的不是我们知道什么,
而是我们怎么知道什么.
—毕达哥拉斯
教练的烦恼
如果要从甲、乙、丙三名选手中选拔一名参加射击比赛?将如何选拔?
甲:3、5、6、7、9
乙:4、5、6、7、8
丙:3、6、6、6、9
方案一:求平均数
甲:3、5、6、7、9
乙:4、5、6、7、8
丙:3、6、6、6、9
方案二:画折线图
问题1
甲:3、5、6、7、9
乙:4、5、6、7、8
丙:3、6、6、6、9
方案三:最大值-最小值
9-3=6
8-4=4
9-3=6
方案四:成绩与平均成绩的偏差和
第一次 第二次 第三次 第四次 第五次 求和
甲 射击成绩 3 5 6 7 9
每次成绩与平均成绩之差 -3 -1 0 1 3
0
乙 射击成绩 4 5 6 7 8
每次成绩与平均成绩之差 -2 -1 0 1 2
0
丙 射击成绩 3 6 6 6 9
每次成绩与平均成绩之差 -3 0 0 0 3
0
去掉负号
↓
↓
绝对值
平方
教师引导,学生独立思考,合作交流
第一次 第二次 第三次 第四次 第五次 求和
甲 射击成绩 3 5 6 7 9
每次成绩与平均成绩之差的绝对值 3 1 0 1 3
8
乙 射击成绩 4 5 6 7 8
每次成绩与平均成绩之差的绝对值 2 1 0 1 2
6
丙 射击成绩 3 6 6 6 9
每次成绩与平均成绩之差的绝对值 3 0 0 0 3
6
方案五:成绩与平均成绩差的绝对值和
没有拉大数据间的差距
第一次 第二次 第三次 第四次 第五次 求和
甲 射击成绩 3 5 6 7 9
每次成绩与平均成绩之差的平方 9 1 0 1 9
20
乙 射击成绩 4 5 6 7 8
每次成绩与平均成绩之差的平方 4 1 0 1 4
10
丙 射击成绩 3 6 6 6 9
每次成绩与平均成绩之差的平方 9 0 0 0 9
18
方案六:成绩与平均成绩差的平方和
“差的平方和”
1 2 3 4 5 6 7 8 9 10 和
乙 成绩 4 5 6 7 8 4 5 6 7 8
4 1 0 1 4 4 1 0 1 4 20
丙 成绩 3 6 6 6 9 ∕ ∕ ∕ ∕ ∕
9 0 0 0 9 18
乙的数据多
再平均
各偏差的平方和的大小还与射击次数有关
知识要点
2.方差的意义:
方差用来衡量一组数据的离散程度(即这组数据偏离平均数的大小).
方差越大,数据的波动越大;
方差越小,数据的波动越小.
(先平均,再求差,后平方,再平均)
1.方差的公式:
知识延伸
数据单位与方差的单位不一致,
为了使单位一致,可用方差的算术平方根来表示
把它叫作标准差.
感谢您的聆听!
欢迎批评指正!
三数一方争天下
说教材 道本质
促成长 拓思维
华为创始人任正非在接受
央视《面对面》采访时表示,
人工智能就是统计学,
大数据就是统计.
统计是研究如何合理地收集、整理、分析数据的科学,它可以为人们制定决策提供依据.
第20章 数据的整理与初步处理
目录
二 课标要求
四 教学建议
一 教材地位作用
三 教材分析
、
、
、
、
目录
二 课标要求
四 教学建议
一 教材地位作用
三 教材分析
、
、
、
、
初中数学知识树
统计与概率知识树
20章 知 识 结 构
处理数据
刻画一组数据集中趋势的指标
刻画一组数据离散程度的指标
加权平均数
平均数
中位数
众数
用计算器求平均数
方差
用计算器求方差
合理选用平均数、
中位数和众数
目录
二 课标要求
四 教学建议
一 教材地位作用
三 教材分析
、
、
、
、
数学六大核心素养
数学抽象
逻辑推理
数学建模
数学运算
直观想象
数据分析
数感
符号意识
空间观念
几何直观
统计观念
运算能力
推理能力
模型思想
应用意识
创新意识
数学十大思维
统计观念
数据分析观念
目录
二 课标要求
四 教学建议
一 教材地位作用
三 教材分析
、
、
、
、
1. 课时分配
第1课时 20.1.1平均数的意义
第2课时 20.1.2用计算器求平均数
第3课时 20.1.3加权平均数
第4课时 20.2.1中位数和众数
第5课时 20.2.2平均数、中位数和众数的选用
第6课时 20. 3方差
第7课时 数据的离散程度
第20章复习
三、教材分析
2. 重难点分析
目录
二 课标要求
四 教学建议
一 教材地位作用
三 教材分析
、
、
、
、
难点突破一:“权”与“权重”
日常生活中,我们常用平均数表示一组数据的“一般水平”.
一般地,如果有 n 个数据 x1,x2,…,xn,我们用 表示这组数据的平均数,即
先求和,再平分.
求平均数的步骤:
7
6
5
4
3
2
1
A B C D
平均数
先总后均
移多补少
如图ABCD四个杯子中装了不同数量的小球,你能让四个杯子中的小球数目相同吗?
一般水平
超过平均数的总量等于不足平均数的总量
加权平均数
1.什么是权?
2.为什么要加权?
4.加权平均数与算术平均数有什么联系?
3.权和权重一样吗?
北京版七下教材:
“权”
北师版八上教材
人教版八下
华师版八下教参
例如:有5个数据2,2,2,8,8,
求平均数?
权
权重
权
形异质同
在实际问题中,一组数据里的各个数据的“重要程度” 未必相同.因而,在计算这组数据的平均数时,往往给每个数据一个“权”.
教学中应例举与学生生活实际,紧密相关的例子,可以让学生更好地体会加权平均数的意义.
为什么要加权?
教学建议:
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应聘者进行了听、说、读、写的英语水平测试,他们的各项成绩如表所示:
(1)如果公司想招一名综合能力较强的翻译,应该录用谁?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
合作探究
入情入境
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应聘者进行了听、说、读、写的英语水平测试,他们的各项成绩如表所示:
(2)如果公司想招一名笔译能力较强的翻译,用平均数来衡量他们的成绩合理吗?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
合作探究
听、说、读、写的成绩按照2:1:3:4的比确定.
探索合作
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应聘者进行了听、说、读、写的英语水平测试,他们的各项成绩如表所示:
(3)如果公司想招一名口语能力较强的翻译,怎么办?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
合作探究
听、说、读、写的成绩按照3:3:2:2的比确定.
方法反思
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应聘者进行了听、说、读、写的英语水平测试,他们的各项成绩如表所示:
(4)如果你是公司招聘的负责人,你将如何设置权重呢?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
合作探究
我能行,我做主!
叫做加权平均数,其中f1,f2,……,fk叫做权重.
加权平均数:如果n个数中,x1出现f1次,x2出现f2次,……,xk出现fk次,(这里f1+f2+……+fk=n),那么,根据平均数的定义,这n个数的平均数可以表示为
这样求得的平均数
加权平均数
算术平均数
权相等
当权相等时,设
难点突破二:
三数的合理选用
平均数反映了数据的“ 一般 水平”;
中位数反映了数据的“中等水平”;
众数反映了数据的“ 多数水平”.
选取多个统计量,综合分析
【教材144页问题2】八年级某班的教室里,三位同学正在为谁的数学成绩最好而争论,他们的五次数学成绩分别是:
小华: 62, 94, 95, 98, 98.
小明: 62, 62, 98, 99, 100.
小丽: 40, 62, 85, 99, 99.
他们都认为自己的成绩比另两位同学好,你看呢 完成下表:
平均数 中位数 众数
小华 89.4 95 98
小明 84.2 98 62
小丽 77 85 99
三数易错点归纳
① 忽略了加权平均数中“权”的存在
例:有8个数的平均数是10,还有12个数的平均数是12,则这20个数的平均数是 .
【错解】
(两个平均数所占权重是不同的,计算时要体现权重的存在)
【正解】
这20个数的平均数是11.2
② 求中位数时忽略了将数据排序
例:学校8名学生三月份参加义务劳动的时间(小时)分别为3,6,4,3,7,5,7,4,这组数据的中位数是 .
【错解】观察数据可得,中位数为第4、第5个位置的数据的平均数,即
【正解】先将数据进行排序:3,3,4,4,5,6,
7,7,因此中位数为
③忽略了数据的个数
例:广州某地连续10天的最高气温统计如下:
这组数据的中位数是 .
【错解】由图表可得5个温度:22、23、24、25、26,中间位置的数为24,所以中位数为24.
【正解】图表中22、23、24、25、26只是属于最高温度的类型,需要讨论的数据其实有10个:22、23、23、24、24、25、25、25、25、26,因此这组数据的中位数是
最高气温( C) 22 23 24 25 26
天数 1 2 2 4 1
④ 忽略了众数的个数
例:若数据8,7,8,x,5的平均数是7,则这组数据的众数是 .
本题很容易只写出一个众数,漏掉了另外一个.
【正解】由题意可得
,所以,x=7,故这组数据的众数为7、8.
难点突破三:方差的探索
在数学的天地里,重要的不是我们知道什么,
而是我们怎么知道什么.
—毕达哥拉斯
教练的烦恼
如果要从甲、乙、丙三名选手中选拔一名参加射击比赛?将如何选拔?
甲:3、5、6、7、9
乙:4、5、6、7、8
丙:3、6、6、6、9
方案一:求平均数
甲:3、5、6、7、9
乙:4、5、6、7、8
丙:3、6、6、6、9
方案二:画折线图
问题1
甲:3、5、6、7、9
乙:4、5、6、7、8
丙:3、6、6、6、9
方案三:最大值-最小值
9-3=6
8-4=4
9-3=6
方案四:成绩与平均成绩的偏差和
第一次 第二次 第三次 第四次 第五次 求和
甲 射击成绩 3 5 6 7 9
每次成绩与平均成绩之差 -3 -1 0 1 3
0
乙 射击成绩 4 5 6 7 8
每次成绩与平均成绩之差 -2 -1 0 1 2
0
丙 射击成绩 3 6 6 6 9
每次成绩与平均成绩之差 -3 0 0 0 3
0
去掉负号
↓
↓
绝对值
平方
教师引导,学生独立思考,合作交流
第一次 第二次 第三次 第四次 第五次 求和
甲 射击成绩 3 5 6 7 9
每次成绩与平均成绩之差的绝对值 3 1 0 1 3
8
乙 射击成绩 4 5 6 7 8
每次成绩与平均成绩之差的绝对值 2 1 0 1 2
6
丙 射击成绩 3 6 6 6 9
每次成绩与平均成绩之差的绝对值 3 0 0 0 3
6
方案五:成绩与平均成绩差的绝对值和
没有拉大数据间的差距
第一次 第二次 第三次 第四次 第五次 求和
甲 射击成绩 3 5 6 7 9
每次成绩与平均成绩之差的平方 9 1 0 1 9
20
乙 射击成绩 4 5 6 7 8
每次成绩与平均成绩之差的平方 4 1 0 1 4
10
丙 射击成绩 3 6 6 6 9
每次成绩与平均成绩之差的平方 9 0 0 0 9
18
方案六:成绩与平均成绩差的平方和
“差的平方和”
1 2 3 4 5 6 7 8 9 10 和
乙 成绩 4 5 6 7 8 4 5 6 7 8
4 1 0 1 4 4 1 0 1 4 20
丙 成绩 3 6 6 6 9 ∕ ∕ ∕ ∕ ∕
9 0 0 0 9 18
乙的数据多
再平均
各偏差的平方和的大小还与射击次数有关
知识要点
2.方差的意义:
方差用来衡量一组数据的离散程度(即这组数据偏离平均数的大小).
方差越大,数据的波动越大;
方差越小,数据的波动越小.
(先平均,再求差,后平方,再平均)
1.方差的公式:
知识延伸
数据单位与方差的单位不一致,
为了使单位一致,可用方差的算术平方根来表示
把它叫作标准差.
感谢您的聆听!
欢迎批评指正!
