人教版八年级数学下册 19.2-一次函数同步练习(有答案)
文档属性
| 名称 | 人教版八年级数学下册 19.2-一次函数同步练习(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 128.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-19 14:40:06 | ||
图片预览


文档简介
19.2 一次函数
一、单选题
1.一次函数y=x+1不经过的象限是(?????? )
A.?第一象限???????????????????????????B.?第二象限???????????????????????????C.?第三象限???????????????????????????D.?第四象限
2.下列函数中,是一次函数的是(???? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
3.已知一次函数y=kx+b的图象如图,则k、b的符号是(?? )
A.?k>0,b>0?????????????????????B.?k>0,b<0?????????????????????C.?k<0,b>0?????????????????????D.?k<0,b<0
4.直线 与y轴的交点坐标是(? ?)
A.?(4,0)????????????????????????B.?(0,4)????????????????????????C.?(﹣4,0)????????????????????????D.?(0,﹣4)
5.关于函数y=-2x+1,下列结论正确的是(?????)
A.?图象必经过(-2,1)???????????????????????????????????????B.?y随x的增大而增大
C.?图象经过第一、二、三象限????????????????????????????????D.?当x >?时,y<0
6.如图,一次函数图象经过点A,且与正比例函数y=-x的图象交于点B,则该一次函数的表达式为( )
A.?y=-x+2???????????????????????????????B.?y=x+2???????????????????????????????C.?y=x-2???????????????????????????????D.?y=-x-2
7.已知一次函数 . 若 随 的增大而增大,则 的取值范围是(?? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
8.下列函数关系中表示一次函数的有(?? )
①y=2x+1 ②y= ③y= ?–x ④s=60t ⑤ y=100-25x
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
9.已知方程 解是 ,则直线 与 的交点是(???? )
A.?(1,0)?????????????????????????B.?(1,3)?????????????????????????C.?(-1,-1)?????????????????????????D.?(-1,5)
10.若函数y=(a-5)x1-b+b是一次函数,则a、b应满足的条件是( ).
A.?a=5且b≠0???????????????????????B.?a=5且b=0???????????????????????C.?a≠5且b≠0???????????????????????D.?a≠5且b=0
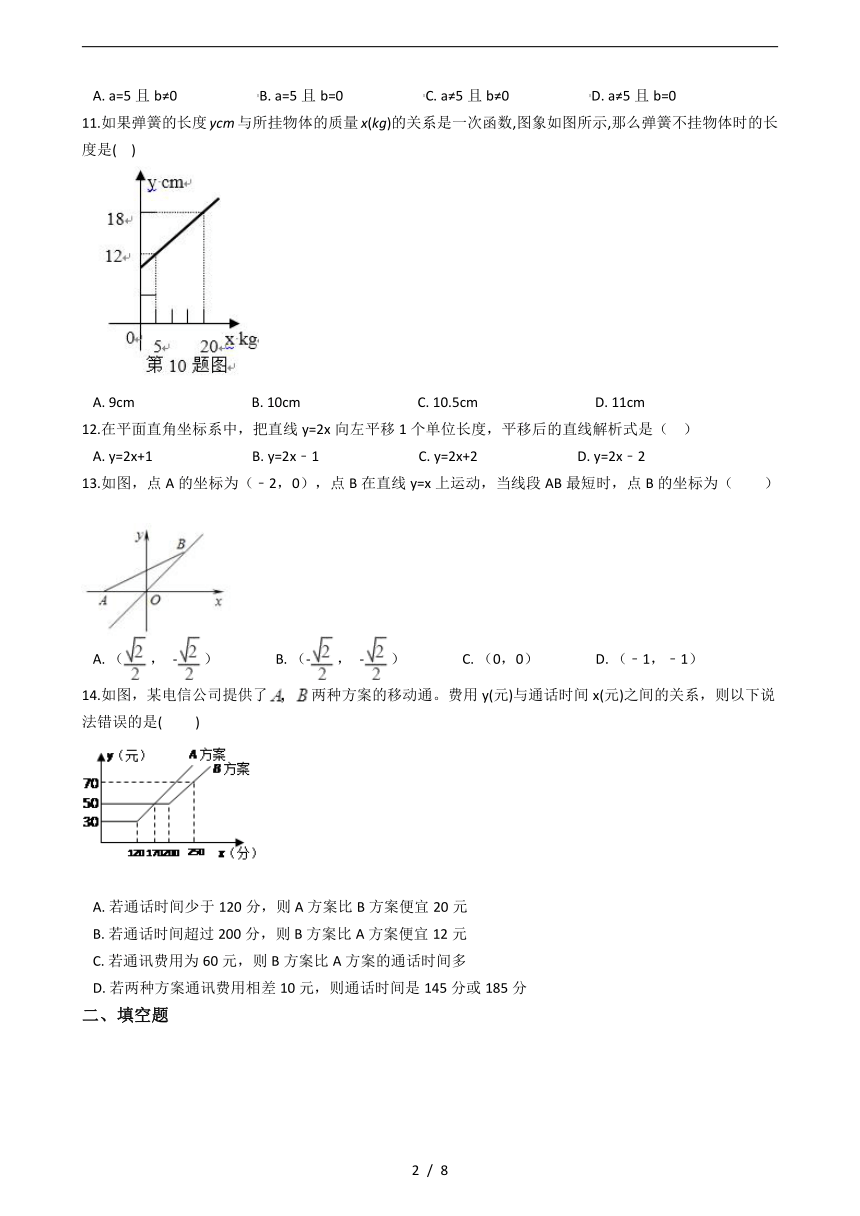
11.如果弹簧的长度ycm与所挂物体的质量x(kg)的关系是一次函数,图象如图所示,那么弹簧不挂物体时的长度是(?? )
A.?9cm??????????????????????????????????B.?10cm??????????????????????????????????C.?10.5cm??????????????????????????????????D.?11cm
12.在平面直角坐标系中,把直线y=2x向左平移1个单位长度,平移后的直线解析式是(?? )
A.?y=2x+1?????????????????????????????B.?y=2x﹣1?????????????????????????????C.?y=2x+2?????????????????????????????D.?y=2x﹣2
13.如图,点A的坐标为(﹣2,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
A.?(, -)????????????????B.?(-, -)????????????????C.?(0,0)????????????????D.?(﹣1,﹣1)
14.如图,某电信公司提供了两种方案的移动通。费用y(元)与通话时间x(元)之间的关系,则以下说法错误的是(? ? ? )
A.?若通话时间少于120分,则A方案比B方案便宜20元
B.?若通话时间超过200分,则B方案比A方案便宜12元
C.?若通讯费用为60元,则B方案比A方案的通话时间多
D.?若两种方案通讯费用相差10元,则通话时间是145分或185分
二、填空题
15.如图,直线y=-x与y=ax+3a(a≠0)的交点的横坐标为-1.5,则关于x的不等式-x>ax+3a>0的整数解为________。
16.若函数 是一次函数,则m=________,且 随 的增大而增大________
17.如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y(元)与通话时间t(分钟)之间的函数关系,则通话8分钟应付电话费________元.
18.直线 与 平行,且经过(2,1),则 + =________。
三、计算题
19.已知函数y=(2m+1)x+m-3
(1)若函数图象经过原点,求m的值;
(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;
(3)若这个函数是一次函数,且图象不经过第四象限, 求的取值范围.
20.在平面直角坐标系中,直线y=kx+3经过(2,7),求不等式kx﹣6≤0的解集.
四、解答题
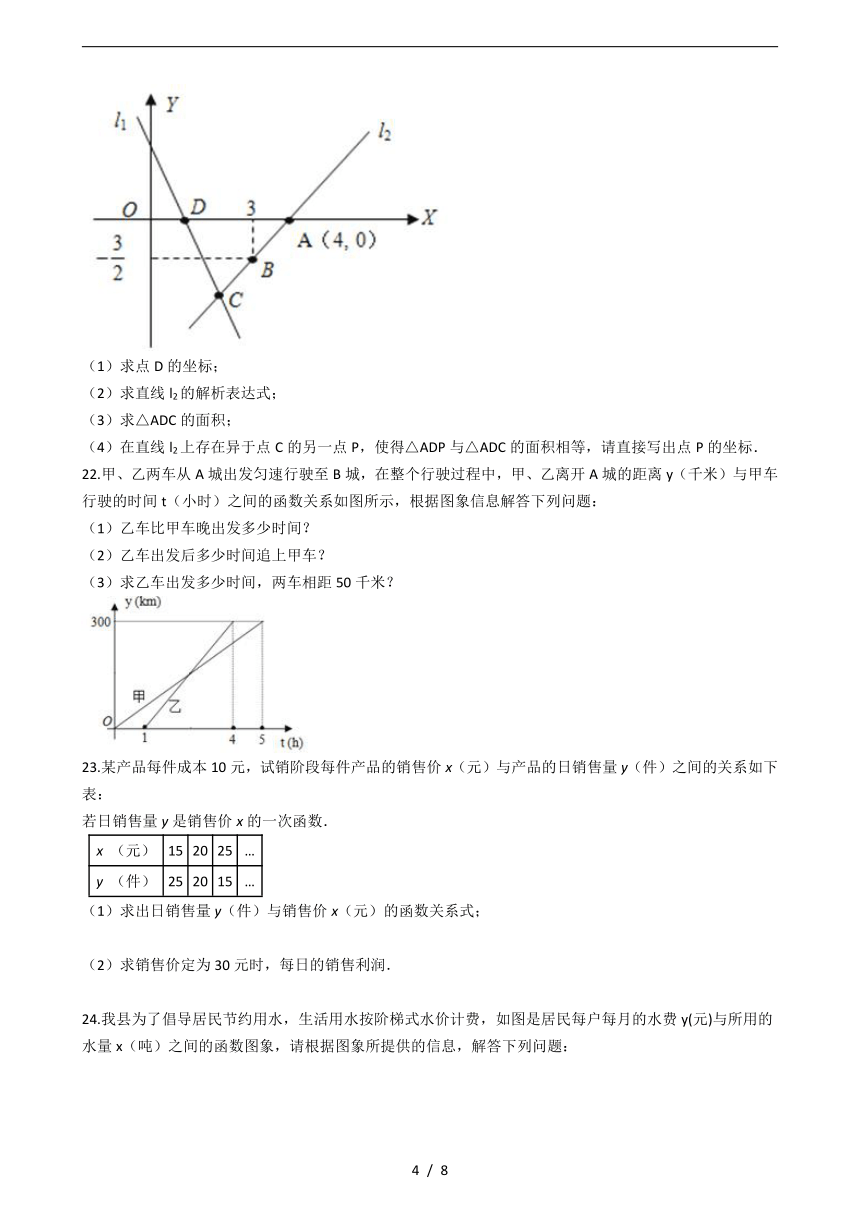
21.如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1 , l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
22.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,根据图象信息解答下列问题:
(1)乙车比甲车晚出发多少时间?
(2)乙车出发后多少时间追上甲车?
(3)求乙车出发多少时间,两车相距50千米?
23.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
若日销售量y是销售价x的一次函数.
x (元) 15 20 25 …
y (件) 25 20 15 …
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
24.我县为了倡导居民节约用水,生活用水按阶梯式水价计费,如图是居民每户每月的水费y(元)与所用的水量x(吨)之间的函数图象,请根据图象所提供的信息,解答下列问题:
(1)当用水量不超过10吨时,每吨水收费多少元?
(2)当用水量超过10吨且不超过30吨时,求y与x之间的函数关系式;
(3)某户居民三、四月份水费共82元,四月份用水比三月份多4吨,求这户居民三月份用水多少吨。
五、综合题
25.某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
答案解析部分
一、单选题
1.【答案】 D 2.【答案】 B 3.【答案】 D 4.【答案】 D 5.【答案】 D
6.【答案】 B 7.【答案】 B 8.【答案】D 9.【答案】 B 10.【答案】 D
11.【答案】 B 12.【答案】 C 13.【答案】 D 14.【答案】 D
二、填空题
15.【答案】-2
16.【答案】m=-1;减小
17.【答案】7.4
18.【答案】6
三、计算题
19.【答案】解:(1)把(0,0)代入,得m-3=0,m=3;
(2)根据y随x的增大而减小说明k<0,即2m+1<0,m<;
(3)若图象经过第一、三象限,得m=3.
若图象经过第一、二、三象限,则2m+1>0,m-3>0,解得m>3,
综上所述:m≥3.
20.【答案】解:∵直线y=kx+3经过(2,7), ∴2k+3=7,
解得:k=2,
∴2x﹣6≤0,
解得:x≤3.
四、解答题
21.【答案】解:(1)由y=﹣3x+3,令y=0,得﹣3x+3=0,
∴x=1,
∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,
由图象知:x=4,y=0;x=3,y=-,代入表达式y=kx+b,
∴ ,
∴,
∴直线l2的解析表达式为y=x-6;
(3)由,
解得,
∴C(2,﹣3),
∵AD=3,
∴S△ADC=×3×|﹣3|=;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到直线AD的距离,即C纵坐标的绝对值=|﹣3|=3,
则P到AD距离=3,
∴P纵坐标的绝对值=3,点P不是点C,
∴点P纵坐标是3,
∵y=1.5x﹣6,y=3,
∴1.5x﹣6=3
x=6,
所以P(6,3).
22.【答案】解:(1)由图象可知乙车比甲车晚出发1个小时.
(2)设甲的函数解析式为y=kx,把点(5,300)代入得到k=60,故y=60x,
设乙的函数解析式为y=k′x+b,把点(1,0)和点(4,300)代入得到解得故y=100x﹣100,
由得,
-1==1.5
所以乙车出发后1.5小时追上甲车.
(3)由题意:60x﹣(100x﹣100)=50或100x﹣100﹣60x=50
解得到x=或,
因为﹣1=,﹣1=,
所以求乙车出发或小时,两车相距50千米.
23.【答案】(1)y=-x+40
(2)解:200元
24.【答案】(1)解:如图,当x=10时,水费是20元,则每吨水费为20÷10=2(元/吨)。
(2)解:当10
?解得
∴直线y=3x-10(10
(3)解:设居民三月份用水x吨,则四月份用水x+4吨,
当x=10时,水费:2×10+3×14-10=52(元)<82元,
故x>10,则水费:3x-10+3(x+4)-10=82,解得x=15,
答:这户居民三月份用水15吨。
五、综合题
25.【答案】 (1)设甲材料每千克x元,乙材料每千克y元,根据购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元,可列出方程组
?,解方程组即可得到甲材料每千克15元,乙材料每千克25元。
(2)设生产A产品m件,生产B产品(50-m)件,先表示出生产这50件产品的材料费为15×30m+25×10m+15×20(50-m)+25×20(50-m)=-100m+40000,根据购买甲、乙两种材料的资金不超过38000元得到-100m+40000≤38000,根据生产B产品不少于28件得到50-m≥28,然后解两个不等式求出其公共部分得到20≤m≤22,而m为整数,则m的值为20,21,22,易得符合条件的生产方案;
(3)设总生产成本为W元,加工费为:200m+300(50-m),根据成本=材料费+加工费得到W=-100m+40000+200m+300(50-m)=-200m+55000,根据一次函数的性质得到W 随m的增大而减小,然后把m=22代入计算,即可得到最低成本.
/
一、单选题
1.一次函数y=x+1不经过的象限是(?????? )
A.?第一象限???????????????????????????B.?第二象限???????????????????????????C.?第三象限???????????????????????????D.?第四象限
2.下列函数中,是一次函数的是(???? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
3.已知一次函数y=kx+b的图象如图,则k、b的符号是(?? )
A.?k>0,b>0?????????????????????B.?k>0,b<0?????????????????????C.?k<0,b>0?????????????????????D.?k<0,b<0
4.直线 与y轴的交点坐标是(? ?)
A.?(4,0)????????????????????????B.?(0,4)????????????????????????C.?(﹣4,0)????????????????????????D.?(0,﹣4)
5.关于函数y=-2x+1,下列结论正确的是(?????)
A.?图象必经过(-2,1)???????????????????????????????????????B.?y随x的增大而增大
C.?图象经过第一、二、三象限????????????????????????????????D.?当x >?时,y<0
6.如图,一次函数图象经过点A,且与正比例函数y=-x的图象交于点B,则该一次函数的表达式为( )
A.?y=-x+2???????????????????????????????B.?y=x+2???????????????????????????????C.?y=x-2???????????????????????????????D.?y=-x-2
7.已知一次函数 . 若 随 的增大而增大,则 的取值范围是(?? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
8.下列函数关系中表示一次函数的有(?? )
①y=2x+1 ②y= ③y= ?–x ④s=60t ⑤ y=100-25x
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
9.已知方程 解是 ,则直线 与 的交点是(???? )
A.?(1,0)?????????????????????????B.?(1,3)?????????????????????????C.?(-1,-1)?????????????????????????D.?(-1,5)
10.若函数y=(a-5)x1-b+b是一次函数,则a、b应满足的条件是( ).
A.?a=5且b≠0???????????????????????B.?a=5且b=0???????????????????????C.?a≠5且b≠0???????????????????????D.?a≠5且b=0
11.如果弹簧的长度ycm与所挂物体的质量x(kg)的关系是一次函数,图象如图所示,那么弹簧不挂物体时的长度是(?? )
A.?9cm??????????????????????????????????B.?10cm??????????????????????????????????C.?10.5cm??????????????????????????????????D.?11cm
12.在平面直角坐标系中,把直线y=2x向左平移1个单位长度,平移后的直线解析式是(?? )
A.?y=2x+1?????????????????????????????B.?y=2x﹣1?????????????????????????????C.?y=2x+2?????????????????????????????D.?y=2x﹣2
13.如图,点A的坐标为(﹣2,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
A.?(, -)????????????????B.?(-, -)????????????????C.?(0,0)????????????????D.?(﹣1,﹣1)
14.如图,某电信公司提供了两种方案的移动通。费用y(元)与通话时间x(元)之间的关系,则以下说法错误的是(? ? ? )
A.?若通话时间少于120分,则A方案比B方案便宜20元
B.?若通话时间超过200分,则B方案比A方案便宜12元
C.?若通讯费用为60元,则B方案比A方案的通话时间多
D.?若两种方案通讯费用相差10元,则通话时间是145分或185分
二、填空题
15.如图,直线y=-x与y=ax+3a(a≠0)的交点的横坐标为-1.5,则关于x的不等式-x>ax+3a>0的整数解为________。
16.若函数 是一次函数,则m=________,且 随 的增大而增大________
17.如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y(元)与通话时间t(分钟)之间的函数关系,则通话8分钟应付电话费________元.
18.直线 与 平行,且经过(2,1),则 + =________。
三、计算题
19.已知函数y=(2m+1)x+m-3
(1)若函数图象经过原点,求m的值;
(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;
(3)若这个函数是一次函数,且图象不经过第四象限, 求的取值范围.
20.在平面直角坐标系中,直线y=kx+3经过(2,7),求不等式kx﹣6≤0的解集.
四、解答题
21.如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1 , l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
22.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,根据图象信息解答下列问题:
(1)乙车比甲车晚出发多少时间?
(2)乙车出发后多少时间追上甲车?
(3)求乙车出发多少时间,两车相距50千米?
23.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
若日销售量y是销售价x的一次函数.
x (元) 15 20 25 …
y (件) 25 20 15 …
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
24.我县为了倡导居民节约用水,生活用水按阶梯式水价计费,如图是居民每户每月的水费y(元)与所用的水量x(吨)之间的函数图象,请根据图象所提供的信息,解答下列问题:
(1)当用水量不超过10吨时,每吨水收费多少元?
(2)当用水量超过10吨且不超过30吨时,求y与x之间的函数关系式;
(3)某户居民三、四月份水费共82元,四月份用水比三月份多4吨,求这户居民三月份用水多少吨。
五、综合题
25.某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
答案解析部分
一、单选题
1.【答案】 D 2.【答案】 B 3.【答案】 D 4.【答案】 D 5.【答案】 D
6.【答案】 B 7.【答案】 B 8.【答案】D 9.【答案】 B 10.【答案】 D
11.【答案】 B 12.【答案】 C 13.【答案】 D 14.【答案】 D
二、填空题
15.【答案】-2
16.【答案】m=-1;减小
17.【答案】7.4
18.【答案】6
三、计算题
19.【答案】解:(1)把(0,0)代入,得m-3=0,m=3;
(2)根据y随x的增大而减小说明k<0,即2m+1<0,m<;
(3)若图象经过第一、三象限,得m=3.
若图象经过第一、二、三象限,则2m+1>0,m-3>0,解得m>3,
综上所述:m≥3.
20.【答案】解:∵直线y=kx+3经过(2,7), ∴2k+3=7,
解得:k=2,
∴2x﹣6≤0,
解得:x≤3.
四、解答题
21.【答案】解:(1)由y=﹣3x+3,令y=0,得﹣3x+3=0,
∴x=1,
∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,
由图象知:x=4,y=0;x=3,y=-,代入表达式y=kx+b,
∴ ,
∴,
∴直线l2的解析表达式为y=x-6;
(3)由,
解得,
∴C(2,﹣3),
∵AD=3,
∴S△ADC=×3×|﹣3|=;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到直线AD的距离,即C纵坐标的绝对值=|﹣3|=3,
则P到AD距离=3,
∴P纵坐标的绝对值=3,点P不是点C,
∴点P纵坐标是3,
∵y=1.5x﹣6,y=3,
∴1.5x﹣6=3
x=6,
所以P(6,3).
22.【答案】解:(1)由图象可知乙车比甲车晚出发1个小时.
(2)设甲的函数解析式为y=kx,把点(5,300)代入得到k=60,故y=60x,
设乙的函数解析式为y=k′x+b,把点(1,0)和点(4,300)代入得到解得故y=100x﹣100,
由得,
-1==1.5
所以乙车出发后1.5小时追上甲车.
(3)由题意:60x﹣(100x﹣100)=50或100x﹣100﹣60x=50
解得到x=或,
因为﹣1=,﹣1=,
所以求乙车出发或小时,两车相距50千米.
23.【答案】(1)y=-x+40
(2)解:200元
24.【答案】(1)解:如图,当x=10时,水费是20元,则每吨水费为20÷10=2(元/吨)。
(2)解:当10
?解得
∴直线y=3x-10(10
(3)解:设居民三月份用水x吨,则四月份用水x+4吨,
当x=10时,水费:2×10+3×14-10=52(元)<82元,
故x>10,则水费:3x-10+3(x+4)-10=82,解得x=15,
答:这户居民三月份用水15吨。
五、综合题
25.【答案】 (1)设甲材料每千克x元,乙材料每千克y元,根据购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元,可列出方程组
?,解方程组即可得到甲材料每千克15元,乙材料每千克25元。
(2)设生产A产品m件,生产B产品(50-m)件,先表示出生产这50件产品的材料费为15×30m+25×10m+15×20(50-m)+25×20(50-m)=-100m+40000,根据购买甲、乙两种材料的资金不超过38000元得到-100m+40000≤38000,根据生产B产品不少于28件得到50-m≥28,然后解两个不等式求出其公共部分得到20≤m≤22,而m为整数,则m的值为20,21,22,易得符合条件的生产方案;
(3)设总生产成本为W元,加工费为:200m+300(50-m),根据成本=材料费+加工费得到W=-100m+40000+200m+300(50-m)=-200m+55000,根据一次函数的性质得到W 随m的增大而减小,然后把m=22代入计算,即可得到最低成本.
/
