人教B版(2019)数学必修(第三册):7.2.4 诱导公式 教案
文档属性
| 名称 | 人教B版(2019)数学必修(第三册):7.2.4 诱导公式 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 32.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-20 00:00:00 | ||
图片预览

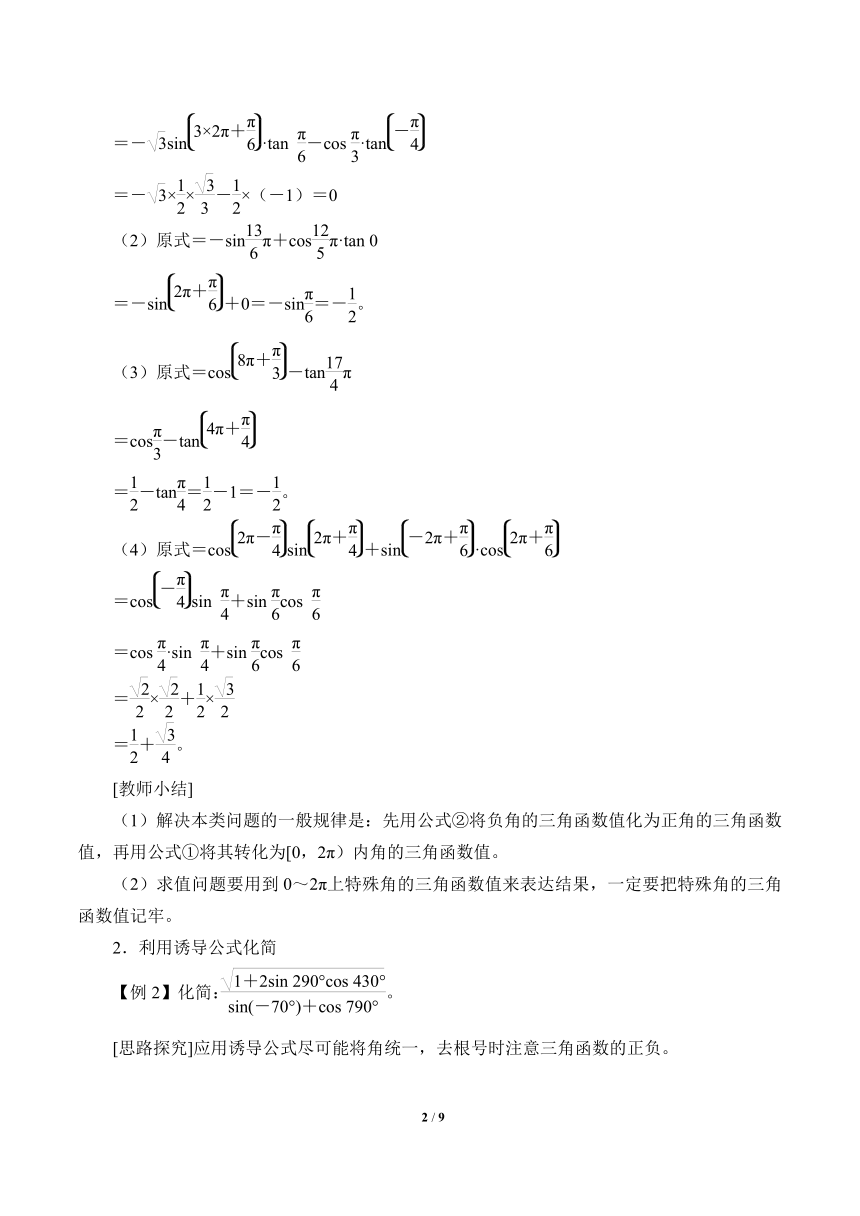


文档简介
诱导公式
第一课时
教学目标 核心素养
1.掌握诱导公式①、②,并会用公式求任意角的三角函数值。(重点) 2.会用诱导公式一、二进行简单的三角求值、化简与恒等式的证明。(难点) 1.通过诱导公式①和诱导公式②的推导,培养学生的逻辑推理核心素养。 2.借助诱导公式的应用,培养学生的数学运算和逻辑推理核心素养。
【教学过程】
一、问题导入
如果已知sin26°=m,你能用m表示出sin386°,sin(-26),sin154°,sin206°,cos64°吗?你还能用m表示出更多角的三角函数值吗?
这里我们将研究任意角的三角函数值之间的一些特殊关系。
二、新知探究
1.利用诱导公式求值
【例1】计算:
(1)sintan π-cos π·tan;
(2)sin+cosπ·tan 4π;
(3)cosπ+tan;
(4)cossin+sincos。
[思路探究]先化负角为正角,再将大于360°的角化为0°到360°内的角,进而利用诱导公式求得结果。
解:(1)原式=·tan-cos ·tan
=-sin·tan -cos ·tan
=-××-×(-1)=0
(2)原式=-sinπ+cosπ·tan 0
=-sin+0=-sin=-。
(3)原式=cos-tanπ
=cos-tan
=-tan=-1=-。
(4)原式=cossin+sin·cos
=cossin +sin cos
=cos ·sin +sin cos
=×+×
=+。
[教师小结]
(1)解决本类问题的一般规律是:先用公式②将负角的三角函数值化为正角的三角函数值,再用公式①将其转化为[0,2π)内角的三角函数值。
(2)求值问题要用到0~2π上特殊角的三角函数值来表达结果,一定要把特殊角的三角函数值记牢。
2.利用诱导公式化简
【例2】化简:。
[思路探究]应用诱导公式尽可能将角统一,去根号时注意三角函数的正负。
解:原式=
==
==-1.
[教师小结]
(1)三角函数式的化简常用诱导公式将任意角的三角函数转化为锐角的三角函数。
(2)化简时要特别注意“1”的变形应用。
三、课堂总结
1.诱导公式的记忆
诱导公式①、②的记忆口诀是“函数名不变,符号看象限”。其含义是诱导公式两边的函数名称一致,符号则是将α看成锐角时原角所在象限的三角函数值的符号。α看成锐角,只是公式记忆的方便,实际上α可以是任意角。
2.利用诱导公式①、②,还可以得出如下公式
sin(2π-α)=-sin α,
cos(2π-α)=cos α,
tan(2π-α)=-tan α。
四、课堂检测
1.sin 690°的值为( )。
A. B.
C.- D.-
【答案】C
【解析】sin 690°=sin(720°-30°)=-sin 30°=-。
2.点P(cos 2 019°,sin 2 019°)落在( )。
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【答案】C
【解析】∵2019°=6×360°-141°,
∴cos2019°=cos(-141°)=cos 141°<0,
sin2019°=sin(-141°)=-sin 141°<0,
∴点P在第三象限。
3.的化简结果为________。
【答案】1
【解析】原式==1。
4.求下列各式的值:
(1)cosπ+tan;
(2)sin810°+tan1125°+cos420°。
解:(1)cosπ+tan
=cos+tan=cos+tan=+1=。
(2)原式=sin(2×360°+90°)+tan(3×360°+45°)+cos(360°+60°)=sin 90°+tan 45°+cos 60°=1+1+=。
第二课时
教学目标 核心素养
1.掌握诱导公式③~⑧,能正确运用这些公式求任意角的三角函数值。(重点) 2.能运用诱导公式进行简单的三角函数的化简与恒等式的证明。(难点) 1.通过诱导公式的推导,培养学生的逻辑推理核心素养。 2.通过诱导公式的应用,提升学生的逻辑推理及数学运算核心素养。
【教学过程】
一、问题导入
对于任意一个角α来说,α与π-α的终边有什么关系?由此你能得到它们的正弦、余弦、正切之间的关系吗?
二、新知探究
1.给角求值问题
【例1】(1)求下列各三角函数值。
①sin;②cos π;
(2)求sin ·cos (n ∈ Z)的值。
[思路探究](1)直接利用诱导公式求解,注意公式的灵活选择。
(2)分n为奇数、偶数两种情况讨论。
解:(1)①sin
=-sin =-sin=-sin =-sin=sin =。
②cos π=cos=cos =cos=-cos =-。
(2)①当n为奇数时,
原式=sin ·=sin
=sin ·cos =×=;
②当n为偶数时,原式=sin π·cos π
=sin ·cos
=sin ·
=×=-。
=sin
=cos=。
[教师小结]
(1)已知角求值的问题主要是利用诱导公式把任意角的三角函数值转化为锐角的三角函数值求解。一般是先利用公式②将负角化为正角,再利用公式①将任意角转化为0°~360°之间的角,然后利用公式③、公式④转化为0°~90°之间的角求解。
(2)凡涉及参数n的三角函数求值问题。由于n为奇数、偶数时,三角函数值有所不同,故考虑对n进行分类讨论。其次,熟记诱导公式,熟悉各诱导公式的作用也是解题的关键。
2.给值(式)求值问题
【例2】已知cos(π+α)=-,求cos的值。
[思路探究]→→
解:∵cos(π+α)=-cos α=-,
∴cos α=,
∴α为第一或第四象限角。
①若α为第一象限角,
则cos=-sin α=-
=-=-。
②若α为第四象限角,
则cos=-sin α=
==。
[教师小结]
(1)已知一个角的某种三角函数值,求这个角的其他三角函数值,若给定具体数值,但未指定角α的取值范围,就要进行讨论。
(2)常见的互余关系有:-α与+α;+α与-α;+α与-α等。
(3)常见的互补关系有:+θ与-θ;+θ与-θ等。
3.诱导公式中的分类讨论思想
[探究问题]
(1)利用诱导公式能否直接写出sin(kπ+α)的值?
【提示】不能。因为k是奇数还是偶数不确定。
当k是奇数时,即k=2n+1(n ∈ Z),sin(kπ+α)=sin(π+α)=-sin α;
当k是偶数时,即k=2n(n ∈ Z),sin(kπ+α)=sin α。
(2)如何化简tan呢?
【提示】当k为奇数时,即k=2n+1(n ∈ Z),
tan=tan===;
当k为偶数时,即k=2n(n ∈ Z),
tan=tan α。
综上,tan=
【例3】设k为整数,化简:。
[思路探究]分k为奇数,k为偶数两种情况分别求解或利用角的交换求解。
解:当k为偶数时,
==-1.
当k为奇数时
==-1.
综上可得=-1.
[教师小结]
本题主要考查分类讨论的思想以及诱导公式。常用的解决方法有两种:①为了便于运用诱导公式,必须把k分成偶数和奇数两种情况讨论;②观察式子结构,kπ-α+kπ+α=2kπ,k+1π+α+k-1π-α=2kπ,可使用配角法。
三、课堂总结
1.诱导公式可归纳为
“k·±α(k ∈ Z)”的三角函数值与α的三角函数值之间的关系。当k为偶数时得角α的同名三角函数值,当k为奇数时得角α的异名三角函数值。然后在前面加上一个把角α看成锐角时原三角函数值的符号。可简记为“奇变偶不变,符号看象限”。
2.诱导公式是三角变换的基本公式,其中角可以是一个单角,也可以是一个复角,应用时要注意整体把握,灵活变通。
四、课堂检测
1.下列各式不正确的是( )。
A.sin(α+180°)=-sin α
B、Cos(-α+β)=-cos(α-β)
C.sin(-α-360°)=-sin α
D.cos(-α-β)=cos(α+β)
【答案】B
【解析】cos(-α+β)=cos[-(α-β)]=cos(α-β),故B项错误。
2.sin 600°的值为( )。
A. B.-
C. D.-
【答案】D
【解析】sin 600°=sin(720°-120°)=-sin 120°
=-sin(180°-60°)=-sin 60°=-。故选D.
3.cos 1 030°=( )。
A.cos 50° B.-cos 50°
C.sin 50° D.-sin 50°
【答案】A
【解析】cos1030°=cos(3×360°-50°)=cos(-50°)=cos 50°。
4.已知sin φ=,求cos+sin(3π-φ)的值。
解:∵sin φ=,
∴cos=cos
=cos=cos=sin φ=,
∴cos+sin(3π-φ)=+sin(π-φ)
=+sin φ=。
8 / 8
第一课时
教学目标 核心素养
1.掌握诱导公式①、②,并会用公式求任意角的三角函数值。(重点) 2.会用诱导公式一、二进行简单的三角求值、化简与恒等式的证明。(难点) 1.通过诱导公式①和诱导公式②的推导,培养学生的逻辑推理核心素养。 2.借助诱导公式的应用,培养学生的数学运算和逻辑推理核心素养。
【教学过程】
一、问题导入
如果已知sin26°=m,你能用m表示出sin386°,sin(-26),sin154°,sin206°,cos64°吗?你还能用m表示出更多角的三角函数值吗?
这里我们将研究任意角的三角函数值之间的一些特殊关系。
二、新知探究
1.利用诱导公式求值
【例1】计算:
(1)sintan π-cos π·tan;
(2)sin+cosπ·tan 4π;
(3)cosπ+tan;
(4)cossin+sincos。
[思路探究]先化负角为正角,再将大于360°的角化为0°到360°内的角,进而利用诱导公式求得结果。
解:(1)原式=·tan-cos ·tan
=-sin·tan -cos ·tan
=-××-×(-1)=0
(2)原式=-sinπ+cosπ·tan 0
=-sin+0=-sin=-。
(3)原式=cos-tanπ
=cos-tan
=-tan=-1=-。
(4)原式=cossin+sin·cos
=cossin +sin cos
=cos ·sin +sin cos
=×+×
=+。
[教师小结]
(1)解决本类问题的一般规律是:先用公式②将负角的三角函数值化为正角的三角函数值,再用公式①将其转化为[0,2π)内角的三角函数值。
(2)求值问题要用到0~2π上特殊角的三角函数值来表达结果,一定要把特殊角的三角函数值记牢。
2.利用诱导公式化简
【例2】化简:。
[思路探究]应用诱导公式尽可能将角统一,去根号时注意三角函数的正负。
解:原式=
==
==-1.
[教师小结]
(1)三角函数式的化简常用诱导公式将任意角的三角函数转化为锐角的三角函数。
(2)化简时要特别注意“1”的变形应用。
三、课堂总结
1.诱导公式的记忆
诱导公式①、②的记忆口诀是“函数名不变,符号看象限”。其含义是诱导公式两边的函数名称一致,符号则是将α看成锐角时原角所在象限的三角函数值的符号。α看成锐角,只是公式记忆的方便,实际上α可以是任意角。
2.利用诱导公式①、②,还可以得出如下公式
sin(2π-α)=-sin α,
cos(2π-α)=cos α,
tan(2π-α)=-tan α。
四、课堂检测
1.sin 690°的值为( )。
A. B.
C.- D.-
【答案】C
【解析】sin 690°=sin(720°-30°)=-sin 30°=-。
2.点P(cos 2 019°,sin 2 019°)落在( )。
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【答案】C
【解析】∵2019°=6×360°-141°,
∴cos2019°=cos(-141°)=cos 141°<0,
sin2019°=sin(-141°)=-sin 141°<0,
∴点P在第三象限。
3.的化简结果为________。
【答案】1
【解析】原式==1。
4.求下列各式的值:
(1)cosπ+tan;
(2)sin810°+tan1125°+cos420°。
解:(1)cosπ+tan
=cos+tan=cos+tan=+1=。
(2)原式=sin(2×360°+90°)+tan(3×360°+45°)+cos(360°+60°)=sin 90°+tan 45°+cos 60°=1+1+=。
第二课时
教学目标 核心素养
1.掌握诱导公式③~⑧,能正确运用这些公式求任意角的三角函数值。(重点) 2.能运用诱导公式进行简单的三角函数的化简与恒等式的证明。(难点) 1.通过诱导公式的推导,培养学生的逻辑推理核心素养。 2.通过诱导公式的应用,提升学生的逻辑推理及数学运算核心素养。
【教学过程】
一、问题导入
对于任意一个角α来说,α与π-α的终边有什么关系?由此你能得到它们的正弦、余弦、正切之间的关系吗?
二、新知探究
1.给角求值问题
【例1】(1)求下列各三角函数值。
①sin;②cos π;
(2)求sin ·cos (n ∈ Z)的值。
[思路探究](1)直接利用诱导公式求解,注意公式的灵活选择。
(2)分n为奇数、偶数两种情况讨论。
解:(1)①sin
=-sin =-sin=-sin =-sin=sin =。
②cos π=cos=cos =cos=-cos =-。
(2)①当n为奇数时,
原式=sin ·=sin
=sin ·cos =×=;
②当n为偶数时,原式=sin π·cos π
=sin ·cos
=sin ·
=×=-。
=sin
=cos=。
[教师小结]
(1)已知角求值的问题主要是利用诱导公式把任意角的三角函数值转化为锐角的三角函数值求解。一般是先利用公式②将负角化为正角,再利用公式①将任意角转化为0°~360°之间的角,然后利用公式③、公式④转化为0°~90°之间的角求解。
(2)凡涉及参数n的三角函数求值问题。由于n为奇数、偶数时,三角函数值有所不同,故考虑对n进行分类讨论。其次,熟记诱导公式,熟悉各诱导公式的作用也是解题的关键。
2.给值(式)求值问题
【例2】已知cos(π+α)=-,求cos的值。
[思路探究]→→
解:∵cos(π+α)=-cos α=-,
∴cos α=,
∴α为第一或第四象限角。
①若α为第一象限角,
则cos=-sin α=-
=-=-。
②若α为第四象限角,
则cos=-sin α=
==。
[教师小结]
(1)已知一个角的某种三角函数值,求这个角的其他三角函数值,若给定具体数值,但未指定角α的取值范围,就要进行讨论。
(2)常见的互余关系有:-α与+α;+α与-α;+α与-α等。
(3)常见的互补关系有:+θ与-θ;+θ与-θ等。
3.诱导公式中的分类讨论思想
[探究问题]
(1)利用诱导公式能否直接写出sin(kπ+α)的值?
【提示】不能。因为k是奇数还是偶数不确定。
当k是奇数时,即k=2n+1(n ∈ Z),sin(kπ+α)=sin(π+α)=-sin α;
当k是偶数时,即k=2n(n ∈ Z),sin(kπ+α)=sin α。
(2)如何化简tan呢?
【提示】当k为奇数时,即k=2n+1(n ∈ Z),
tan=tan===;
当k为偶数时,即k=2n(n ∈ Z),
tan=tan α。
综上,tan=
【例3】设k为整数,化简:。
[思路探究]分k为奇数,k为偶数两种情况分别求解或利用角的交换求解。
解:当k为偶数时,
==-1.
当k为奇数时
==-1.
综上可得=-1.
[教师小结]
本题主要考查分类讨论的思想以及诱导公式。常用的解决方法有两种:①为了便于运用诱导公式,必须把k分成偶数和奇数两种情况讨论;②观察式子结构,kπ-α+kπ+α=2kπ,k+1π+α+k-1π-α=2kπ,可使用配角法。
三、课堂总结
1.诱导公式可归纳为
“k·±α(k ∈ Z)”的三角函数值与α的三角函数值之间的关系。当k为偶数时得角α的同名三角函数值,当k为奇数时得角α的异名三角函数值。然后在前面加上一个把角α看成锐角时原三角函数值的符号。可简记为“奇变偶不变,符号看象限”。
2.诱导公式是三角变换的基本公式,其中角可以是一个单角,也可以是一个复角,应用时要注意整体把握,灵活变通。
四、课堂检测
1.下列各式不正确的是( )。
A.sin(α+180°)=-sin α
B、Cos(-α+β)=-cos(α-β)
C.sin(-α-360°)=-sin α
D.cos(-α-β)=cos(α+β)
【答案】B
【解析】cos(-α+β)=cos[-(α-β)]=cos(α-β),故B项错误。
2.sin 600°的值为( )。
A. B.-
C. D.-
【答案】D
【解析】sin 600°=sin(720°-120°)=-sin 120°
=-sin(180°-60°)=-sin 60°=-。故选D.
3.cos 1 030°=( )。
A.cos 50° B.-cos 50°
C.sin 50° D.-sin 50°
【答案】A
【解析】cos1030°=cos(3×360°-50°)=cos(-50°)=cos 50°。
4.已知sin φ=,求cos+sin(3π-φ)的值。
解:∵sin φ=,
∴cos=cos
=cos=cos=sin φ=,
∴cos+sin(3π-φ)=+sin(π-φ)
=+sin φ=。
8 / 8
