人教B版(2019)数学必修(第三册):7.4 数学建模活动:周期现象的描述 学案(含答案)
文档属性
| 名称 | 人教B版(2019)数学必修(第三册):7.4 数学建模活动:周期现象的描述 学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 135.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-20 00:00:00 | ||
图片预览




文档简介
数学建模活动:周期现象的描述
【学习目标】
通过体验将实际问题抽象为三角函数模型并用三角函数知识加以解决的过程,逐步提高将实际问题抽象为数学模型的能力——即数学建模思想。
【学习重难点】
能将某些实际问题抽象为数学模型,体会数学建模的过程。
【学习过程】
一、自主学习
1.三角函数模型应用的步骤:
三角函数模型应用即建模问题,根据题意建立三角函数模型,再求出相应的三角函数在某点处的函数值,进而使实际问题得到解决。
步骤可记为:审读题意→建立三角函数式→根据题意求出某点的三角函数值→解决实际问题。
这里的关键是建立数学模型,一般先根据题意设出代表函数,再利用数据求出待定系数,然后写出具体的三角函数解析式。
2.三角函数模型的拟合应用
我们可以利用搜集到的数据,做出相应的“散点图”,通过观察散点图并进行数据拟合,从而获得具体的函数模型,最后利用这个函数模型来解决相应的实际问题。
解答三角函数应用题应注意四点:
(1)三角函数应用题的语言形式多为“文字语言、图形语言、符号语言”并用,阅读理解中要读懂题目所要反映的实际问题的背景,领悟其中的数学本质,列出等量或不等量的关系。
(2)在建立变量关系这一关键步骤上,要充分运用数形结合的思想、图形语言和符号语言并用的思维方式来打开思想解决问题。
(3)实际问题的背景往往比较复杂,而且需要综合应用多门学科的知识才能完成,因此,在应用数学知识解决实际问题时,应当注意从复杂的背景中抽取基本的数学关系,还要调动相关学科知识来帮助解决问题。
(4)实际问题通常涉及复杂的数据,因此往往需要用到计算机或计算器。
基础自测:
二、基础自测
1.商场人流量被定义为每分钟通过入口的人数,五一某商场的人流量满足函数F(t)=50+4sin(t≥0),则在下列哪个时间段内人流量是增加的( )。
A.[0,5]
B.[5,10]
C.[10,15]
D.[15,20]
2.在两个弹簧上各挂一个质量分别为M1和M2的小球,它们做上下自由振动,已知它们在时间t(s)时离开平衡位置的位移s1(cm)和s2(cm)分别由下列两式确定:
s1=5sin,s2=5cos。
则在时间t=时,s1与s2的大小关系是( )。
A.s1>s2
B.s1C.s1=s2
D.不能确定
3.如图是一向右传播的绳波在某一时刻绳子各点的位置图,经过周期后,乙的位置将传播至( )。
A.甲 B.乙 C.丙 D.丁
4.简谐振动y=sin的频率和相位分别是________。
三、素养提升
三角函数在实际生活中的应用:
例1:海水受日月的引力,在一定的时候发生涨落的现象叫潮。一般地,早潮叫潮,晚潮叫汐。在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋。下表是某港口某天的时刻与水深关系的预报。
时刻 水深/m 时刻 水深/m 时刻 水深/m
0:00 5.0 9:18 2.5 18:36 5.0
3:06 7.5 12:24 5.0 21:42 2.5
6:12 5.0 15:30 7.5 24:00 4.0
(1)选用一个函数来近似描述这一天该港口的水深与时间的关系,给出整点时水深的近似数值(精确0.001m)。
(2)一条货船的吃水深度(船底与水面的距离)为4m,安全条例规定至少要有1.5m的安全间隙(船底与洋底的距离),该船这一天何时能进入港口?在港口能呆多久?
(3)某船的吃水深度为4m,安全间隙为1.5m,该船这一天在2:00开始卸货,吃水深度以0.3m/h的速度减少,如果这条船停止卸货后需0.4h才能驶到深水域,那么该船最好在什么时间停止卸货,将船驶向较深的水域?
解析:(1)以时间x(单位:h)为横坐标,水深y(单位:m)为纵坐标,在直角坐标系中画出散点图(图1)。根据图像,可以考虑用函数y=A·sin(ωx+φ)+h刻画水深与时间之间的对应关系。从数据和图像可以得出:
A=2.5,h=5,T=12.4,φ=0;
由T==12.4,得ω=。
所以,这个港口的水深与时间的关系可用函数y=2.5sinx+5近似描述。
由上述关系式易得港口在整点时水深的近似值(表):
时刻 0:00 1:00 2:00 3:00 4:00 5:00
水深/m 5.000 6.213 7.122 7.497 7.245 6.428
时刻 12:00 13:00 14:00 15:00 16:00 17:00
水深/m 4.497 5.748 6.812 7.420 7.420 6.812
时刻 6:00 7:00 8:00 9:00 10:00 11:00
水深/m 5.253 4.014 3.023 2.529 2.656 3.372
时刻 18:00 19:00 20:00 21:00 22:00 23:00
水深/m 5.748 4.497 3.372 2.656 2.529 3.023
(2)货船需要的安全水深为4+1.5=5.5m,所以当y≥5.5时就可以进港。令
2.5sinx+5=5.5,sin x=0.2.
由计算器可得
0.2013579208≈0.2014.
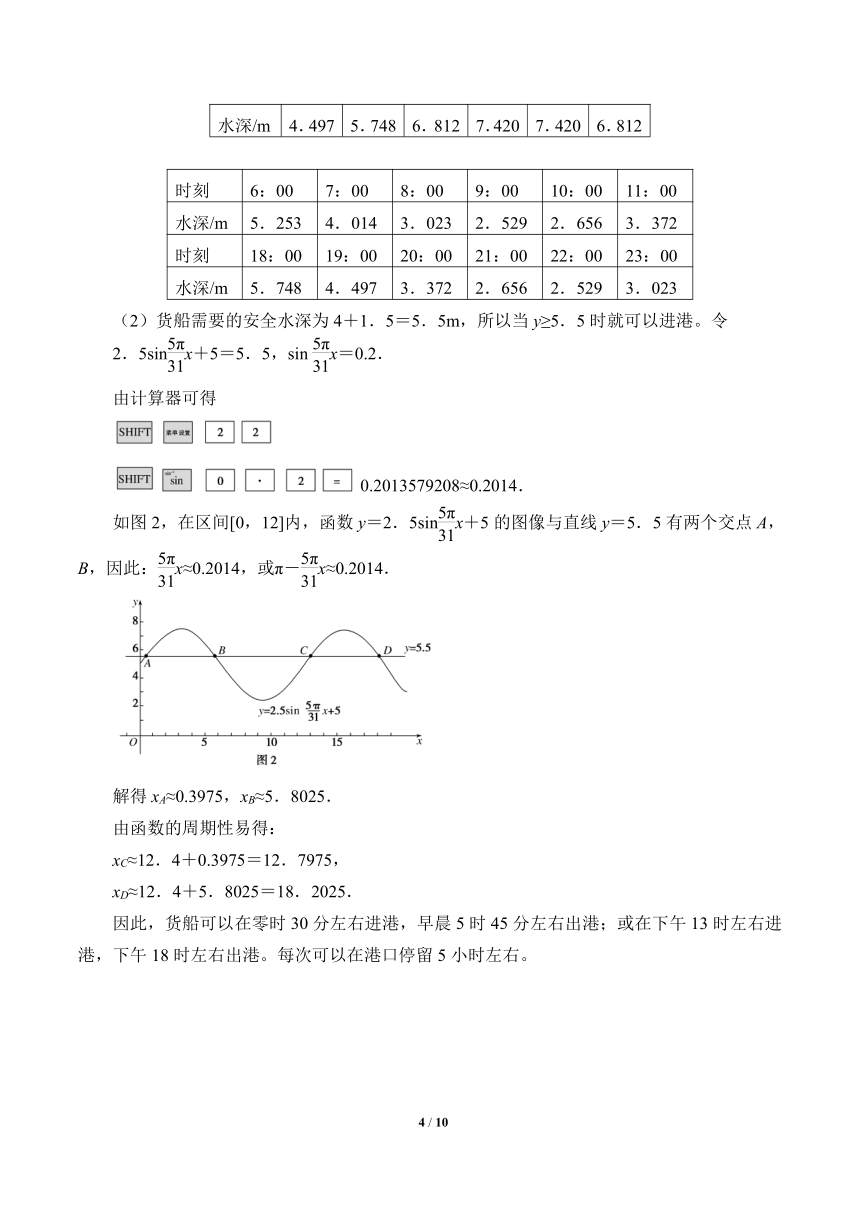
如图2,在区间[0,12]内,函数y=2.5sinx+5的图像与直线y=5.5有两个交点A,B,因此:x≈0.2014,或π-x≈0.2014.
解得xA≈0.3975,xB≈5.8025.
由函数的周期性易得:
xC≈12.4+0.3975=12.7975,
xD≈12.4+5.8025=18.2025.
因此,货船可以在零时30分左右进港,早晨5时45分左右出港;或在下午13时左右进港,下午18时左右出港。每次可以在港口停留5小时左右。
(3)设在xh时货船的安全水深为ym,那么y=5.5-0.3(x-2)(x≥2)。在同一直角坐标系内画出这两个函数的图像,可以看到在6~8时之间两个函数图像有一个交点(图3)。
借助计算工具,用二分法可以求得点P的坐标约为(7.016,3.995),因此为了安全,货船最好在6.6时之前停止卸货,将船驶向较深的水域。
观察问题中所给出的数据,可以看出,水深的变化具有周期性,根据表中的数据画出散点图,从散点图的形状可以判断,这个港口的水深与时间的关系可以用形如y=Asin(ωx+φ)+h的函数来刻画,其中x是时间,y是水深。根据数据可以确定A,ω,φ,h的值。
三、精炼反馈
(一)选择题
1.电流I(A)随时间t(s)变化的关系是I=3sin100πt,t∈[0,+∞),则电流I变化的周期是( )。
A.
B.50
C.
D.100
2.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin+k。据此函数可知,这段时间水深(单位:m)的最大值为( )。
A.5 B.6 C.8 D.10
3.某市某房地产中介对某楼群在今年的房价作了统计与预测,发现每个季度的平均单价y(每平方米的价格,单位:元)与第x季度之间近似满足y=500sin(ωx+φ)+9500(ω>0),已知第1季度和第2季度的平均单价如下表所示。
x 1 2
y 10000 9500
则此楼群在第3季度的平均单价大约是( )。
A.10000元
B.9500元
C.9000元
D.8500元
4.如图,单摆离开平衡位置O的位移s(单位:cm)和时间t(单位:s)的函数关系为s=6sin,则单摆在摆动时,从最右边到最左边的时间为( )。
A.2s
B.1s
C.s
D.s
(二)填空题
5.设某人的血压满足函数式p(t)=115+25sin(160πt),其中p(t)为血压(mmHg),t为时间(min),则此人每分钟心跳的次数是________。
6.有一小球从某点开始来回摆动,离开平衡位置的距离s(单位:cm)关于时间t(单位:s)的函数解析式是s=A·sin(ωt+φ),0<φ<,函数图像如图所示,则φ=________。
7.据市场调查,某种商品每件的售价按月呈f(x)=A·sin(ωx+φ)+B的模型波动(x为月份),已知3月份达到最高价8千元,7月份价格最低,为4千元,则f(x)=________。
(三)解答题
8.弹簧振子以O为平衡位置,在B,C两点间做简谐运动,B,C相距20cm,某时刻振子处在B点,经0.5s振子首次到达C点,求:
(1)振动的振幅、周期和频率;
(2)弹簧振子在5s内通过的路程及位移。
9.交流电的电压E(单位:V)与时间t(单位:s)的关系可用E=220sin(100πt+)来表示,求:
(1)开始时电压;
(2)电压值重复出现一次的时间间隔;
(3)电压的最大值和第一次获得最大值的时间。
答案解析
二、基础自测
1.【答案】C
【解析】由2kπ-≤≤2kπ+,k∈Z,知函数F(t)的增区间为[4kπ-π,4kπ+π],k∈Z。当k=1时,t∈[3π,5π],而[10,15]?[3π,5π],故选C.
2.【答案】C
【解析】当t=时,s1=-5,s2=-5,所以 。
3.【答案】C。
【解析】相邻的最大值与最小值之间间隔区间长度为半个周期,故选C。
4.【答案】,4x+。
【解析】简谐振动y=sin的周期是T==,相位是4x+,频率f==。
三、精炼反馈
1.【答案】A。
【解析】T==。
2.【答案】C。
【解析】由图可知-3+k=2,则k=5,∴y=3sin+5,∴ymax=3+5=8。
3.【答案】C。
【解析】因为y=500sin(ωx+φ)+9500(ω>0),所以当x=1时,500sin(ω+φ)+9500=10000;当x=2时,500sin(2ω+φ)+9500=9500,即
所以易得3ω+φ=-+2kπ,k∈Z。
又当x=3时,y=500sin(3ω+φ)+9500,所以y=9000.
4.【答案】C。
【解析】由题意,知周期T==1(s),从最右边到最左边的时间是半个周期,为s。
5.【答案】80。
【解析】T==(分),f==80(次/分)。
6.【答案】
【解析】根据图像,知,两点的距离刚好是个周期,所以T=-=。
所以T=1,则ω==2π。
因为当t=时,函数取得最大值,
所以2π×+φ=+2kπ,k∈Z,又0<φ<,所以φ=。
7.【答案】f(x)=2sin+6
【解析】由题意得解得A=2,B=6,周期T=2×(7-3)=8,所以ω==。
所以f(x)=2sin+6.
又当x=3时,y=8,
所以8=2sin+6,
所以sin=1,结合|φ|<可得φ=-,
所以f(x)=2sin+6.
8.【答案】(1)设振幅为A,则2A=20cm,
所以A=10cm。
设周期为T,则=0.5s,所以T=1s,所以f=1Hz。
(2)振子在1s内通过的距离为4A,故在5s内通过的路程s=5×4A=20A=20×10=200(cm)。
5s末物体处在B点,所以它的位移为0cm。
9.【答案】(1)当t=0时,E=110(V),
即开始时的电压为110V。
(2)T==(s),即时间间隔为0.02s。
(3)电压的最大值为220V,
当100πt+=,即t=s时第一次取得最大值。
10 / 10
【学习目标】
通过体验将实际问题抽象为三角函数模型并用三角函数知识加以解决的过程,逐步提高将实际问题抽象为数学模型的能力——即数学建模思想。
【学习重难点】
能将某些实际问题抽象为数学模型,体会数学建模的过程。
【学习过程】
一、自主学习
1.三角函数模型应用的步骤:
三角函数模型应用即建模问题,根据题意建立三角函数模型,再求出相应的三角函数在某点处的函数值,进而使实际问题得到解决。
步骤可记为:审读题意→建立三角函数式→根据题意求出某点的三角函数值→解决实际问题。
这里的关键是建立数学模型,一般先根据题意设出代表函数,再利用数据求出待定系数,然后写出具体的三角函数解析式。
2.三角函数模型的拟合应用
我们可以利用搜集到的数据,做出相应的“散点图”,通过观察散点图并进行数据拟合,从而获得具体的函数模型,最后利用这个函数模型来解决相应的实际问题。
解答三角函数应用题应注意四点:
(1)三角函数应用题的语言形式多为“文字语言、图形语言、符号语言”并用,阅读理解中要读懂题目所要反映的实际问题的背景,领悟其中的数学本质,列出等量或不等量的关系。
(2)在建立变量关系这一关键步骤上,要充分运用数形结合的思想、图形语言和符号语言并用的思维方式来打开思想解决问题。
(3)实际问题的背景往往比较复杂,而且需要综合应用多门学科的知识才能完成,因此,在应用数学知识解决实际问题时,应当注意从复杂的背景中抽取基本的数学关系,还要调动相关学科知识来帮助解决问题。
(4)实际问题通常涉及复杂的数据,因此往往需要用到计算机或计算器。
基础自测:
二、基础自测
1.商场人流量被定义为每分钟通过入口的人数,五一某商场的人流量满足函数F(t)=50+4sin(t≥0),则在下列哪个时间段内人流量是增加的( )。
A.[0,5]
B.[5,10]
C.[10,15]
D.[15,20]
2.在两个弹簧上各挂一个质量分别为M1和M2的小球,它们做上下自由振动,已知它们在时间t(s)时离开平衡位置的位移s1(cm)和s2(cm)分别由下列两式确定:
s1=5sin,s2=5cos。
则在时间t=时,s1与s2的大小关系是( )。
A.s1>s2
B.s1
D.不能确定
3.如图是一向右传播的绳波在某一时刻绳子各点的位置图,经过周期后,乙的位置将传播至( )。
A.甲 B.乙 C.丙 D.丁
4.简谐振动y=sin的频率和相位分别是________。
三、素养提升
三角函数在实际生活中的应用:
例1:海水受日月的引力,在一定的时候发生涨落的现象叫潮。一般地,早潮叫潮,晚潮叫汐。在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋。下表是某港口某天的时刻与水深关系的预报。
时刻 水深/m 时刻 水深/m 时刻 水深/m
0:00 5.0 9:18 2.5 18:36 5.0
3:06 7.5 12:24 5.0 21:42 2.5
6:12 5.0 15:30 7.5 24:00 4.0
(1)选用一个函数来近似描述这一天该港口的水深与时间的关系,给出整点时水深的近似数值(精确0.001m)。
(2)一条货船的吃水深度(船底与水面的距离)为4m,安全条例规定至少要有1.5m的安全间隙(船底与洋底的距离),该船这一天何时能进入港口?在港口能呆多久?
(3)某船的吃水深度为4m,安全间隙为1.5m,该船这一天在2:00开始卸货,吃水深度以0.3m/h的速度减少,如果这条船停止卸货后需0.4h才能驶到深水域,那么该船最好在什么时间停止卸货,将船驶向较深的水域?
解析:(1)以时间x(单位:h)为横坐标,水深y(单位:m)为纵坐标,在直角坐标系中画出散点图(图1)。根据图像,可以考虑用函数y=A·sin(ωx+φ)+h刻画水深与时间之间的对应关系。从数据和图像可以得出:
A=2.5,h=5,T=12.4,φ=0;
由T==12.4,得ω=。
所以,这个港口的水深与时间的关系可用函数y=2.5sinx+5近似描述。
由上述关系式易得港口在整点时水深的近似值(表):
时刻 0:00 1:00 2:00 3:00 4:00 5:00
水深/m 5.000 6.213 7.122 7.497 7.245 6.428
时刻 12:00 13:00 14:00 15:00 16:00 17:00
水深/m 4.497 5.748 6.812 7.420 7.420 6.812
时刻 6:00 7:00 8:00 9:00 10:00 11:00
水深/m 5.253 4.014 3.023 2.529 2.656 3.372
时刻 18:00 19:00 20:00 21:00 22:00 23:00
水深/m 5.748 4.497 3.372 2.656 2.529 3.023
(2)货船需要的安全水深为4+1.5=5.5m,所以当y≥5.5时就可以进港。令
2.5sinx+5=5.5,sin x=0.2.
由计算器可得
0.2013579208≈0.2014.
如图2,在区间[0,12]内,函数y=2.5sinx+5的图像与直线y=5.5有两个交点A,B,因此:x≈0.2014,或π-x≈0.2014.
解得xA≈0.3975,xB≈5.8025.
由函数的周期性易得:
xC≈12.4+0.3975=12.7975,
xD≈12.4+5.8025=18.2025.
因此,货船可以在零时30分左右进港,早晨5时45分左右出港;或在下午13时左右进港,下午18时左右出港。每次可以在港口停留5小时左右。
(3)设在xh时货船的安全水深为ym,那么y=5.5-0.3(x-2)(x≥2)。在同一直角坐标系内画出这两个函数的图像,可以看到在6~8时之间两个函数图像有一个交点(图3)。
借助计算工具,用二分法可以求得点P的坐标约为(7.016,3.995),因此为了安全,货船最好在6.6时之前停止卸货,将船驶向较深的水域。
观察问题中所给出的数据,可以看出,水深的变化具有周期性,根据表中的数据画出散点图,从散点图的形状可以判断,这个港口的水深与时间的关系可以用形如y=Asin(ωx+φ)+h的函数来刻画,其中x是时间,y是水深。根据数据可以确定A,ω,φ,h的值。
三、精炼反馈
(一)选择题
1.电流I(A)随时间t(s)变化的关系是I=3sin100πt,t∈[0,+∞),则电流I变化的周期是( )。
A.
B.50
C.
D.100
2.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin+k。据此函数可知,这段时间水深(单位:m)的最大值为( )。
A.5 B.6 C.8 D.10
3.某市某房地产中介对某楼群在今年的房价作了统计与预测,发现每个季度的平均单价y(每平方米的价格,单位:元)与第x季度之间近似满足y=500sin(ωx+φ)+9500(ω>0),已知第1季度和第2季度的平均单价如下表所示。
x 1 2
y 10000 9500
则此楼群在第3季度的平均单价大约是( )。
A.10000元
B.9500元
C.9000元
D.8500元
4.如图,单摆离开平衡位置O的位移s(单位:cm)和时间t(单位:s)的函数关系为s=6sin,则单摆在摆动时,从最右边到最左边的时间为( )。
A.2s
B.1s
C.s
D.s
(二)填空题
5.设某人的血压满足函数式p(t)=115+25sin(160πt),其中p(t)为血压(mmHg),t为时间(min),则此人每分钟心跳的次数是________。
6.有一小球从某点开始来回摆动,离开平衡位置的距离s(单位:cm)关于时间t(单位:s)的函数解析式是s=A·sin(ωt+φ),0<φ<,函数图像如图所示,则φ=________。
7.据市场调查,某种商品每件的售价按月呈f(x)=A·sin(ωx+φ)+B的模型波动(x为月份),已知3月份达到最高价8千元,7月份价格最低,为4千元,则f(x)=________。
(三)解答题
8.弹簧振子以O为平衡位置,在B,C两点间做简谐运动,B,C相距20cm,某时刻振子处在B点,经0.5s振子首次到达C点,求:
(1)振动的振幅、周期和频率;
(2)弹簧振子在5s内通过的路程及位移。
9.交流电的电压E(单位:V)与时间t(单位:s)的关系可用E=220sin(100πt+)来表示,求:
(1)开始时电压;
(2)电压值重复出现一次的时间间隔;
(3)电压的最大值和第一次获得最大值的时间。
答案解析
二、基础自测
1.【答案】C
【解析】由2kπ-≤≤2kπ+,k∈Z,知函数F(t)的增区间为[4kπ-π,4kπ+π],k∈Z。当k=1时,t∈[3π,5π],而[10,15]?[3π,5π],故选C.
2.【答案】C
【解析】当t=时,s1=-5,s2=-5,所以 。
3.【答案】C。
【解析】相邻的最大值与最小值之间间隔区间长度为半个周期,故选C。
4.【答案】,4x+。
【解析】简谐振动y=sin的周期是T==,相位是4x+,频率f==。
三、精炼反馈
1.【答案】A。
【解析】T==。
2.【答案】C。
【解析】由图可知-3+k=2,则k=5,∴y=3sin+5,∴ymax=3+5=8。
3.【答案】C。
【解析】因为y=500sin(ωx+φ)+9500(ω>0),所以当x=1时,500sin(ω+φ)+9500=10000;当x=2时,500sin(2ω+φ)+9500=9500,即
所以易得3ω+φ=-+2kπ,k∈Z。
又当x=3时,y=500sin(3ω+φ)+9500,所以y=9000.
4.【答案】C。
【解析】由题意,知周期T==1(s),从最右边到最左边的时间是半个周期,为s。
5.【答案】80。
【解析】T==(分),f==80(次/分)。
6.【答案】
【解析】根据图像,知,两点的距离刚好是个周期,所以T=-=。
所以T=1,则ω==2π。
因为当t=时,函数取得最大值,
所以2π×+φ=+2kπ,k∈Z,又0<φ<,所以φ=。
7.【答案】f(x)=2sin+6
【解析】由题意得解得A=2,B=6,周期T=2×(7-3)=8,所以ω==。
所以f(x)=2sin+6.
又当x=3时,y=8,
所以8=2sin+6,
所以sin=1,结合|φ|<可得φ=-,
所以f(x)=2sin+6.
8.【答案】(1)设振幅为A,则2A=20cm,
所以A=10cm。
设周期为T,则=0.5s,所以T=1s,所以f=1Hz。
(2)振子在1s内通过的距离为4A,故在5s内通过的路程s=5×4A=20A=20×10=200(cm)。
5s末物体处在B点,所以它的位移为0cm。
9.【答案】(1)当t=0时,E=110(V),
即开始时的电压为110V。
(2)T==(s),即时间间隔为0.02s。
(3)电压的最大值为220V,
当100πt+=,即t=s时第一次取得最大值。
10 / 10
